Compared with the cyclic neural network, NLP application has two layers: embedding layer and softmax layer.

Word Vector Layer
At the input level, each word is represented by a real vector, which is called word embedding, or word embedding. Word vectors can be visually understood as embedding vocabulary into a fixed dimension of real space. Converting word numbers into word vectors has two main functions.
1. Reduce the input dimension. If the word vector is not applicable and the word is directly input into the cyclic neural network in the form of one-hot vector, then the dimension size of the input will be the same as that of the vocabulary, usually more than 10,000. The dimension of word vectors is usually between 200 and 1000, which greatly reduces the number of parameters and computational complexity of the neural network.
2. Increase semantic information. Simple word numbers do not contain any semantic information. The similarity of numbers between two words does not mean that their meanings are related to each other, but the word vectors transform sparse numbers into dense vector representations, which makes it possible for word vectors to contain more abundant information. Word vectors learned in natural language applications usually assign words with similar meanings to their values. Near word vector values make it easier for the upper network to grasp the commonalities between similar words.

Softmax Layer
The last basic chapter has already been described, and it is not repeated here.

Reduce the number of parameters by sharing parameters
The number of parameters in sotfmax layer and word vector layer is directly proportional to the size of the vocabulary. Because the vocabulary values are usually large and HIDDEN_SIZE is relatively small, the number of parameters in the whole neural network is very large.

It has been pointed out that if the parameters of the shared word vector layer and sotfmax layer are used, not only the number of parameters can be greatly reduced, but also the effect of the final model can be improved. This method is implemented in the following code examples.

import numpy as np
import tensorflow as tf

# Training Data Path
TRAIN_DATA = "ptb.train"
# Verify data path
EVAL_DATA = "ptb.valid"
# Test data path
TEST_DATA = "ptb.test"
# Hidden Layer Scale
HIDDEN_SIZE = 300
# Layer Number of LSTM Structure in Deep Cyclic Neural Networks
NUM_LAYERS = 2
# Dictionary size
VOCAB_SIZE = 10000
# The size of training data batch
TRAIN_BATCH_SIZE = 20
# Truncation length of training data
TRAIN_NUM_STEP = 35

# Test data batch size
EVAL_BATCH_SIZE = 1
# Truncation length of test data
EVAL_NUM_STEP = 1
# Number of rounds using training data
NUM_EPOCH = 5
# Probability of LSTM nodes not being dropped out
LSTM_KEEP_PROB = 0.9
# Probability that word vectors are not dropout
EMBEDDING_KEEP_PROB = 0.9
# Upper limit of gradient size for controlling gradient expansion
MAX_GRAD_NORM = 5
# Sharing parameters between Softmax layer and word vector layer
SHARE_EMB_AND_SOFTMAX = True


# The model is described by a PTBModel class, which facilitates the maintenance of the state in the cyclic neural network.
class PTBModel(object):
    def __init__(self, is_training, batch_size, num_steps):
        # The batch size and truncation length used for recording
        self.batch_size = batch_size
        self.num_steps = num_steps

        # Define the input and expected output for each step. Both dimensions are [batch_size, num_steps]
        self.input_data = tf.placeholder(tf.int32, [batch_size, num_steps])
        self.targets = tf.placeholder(tf.int32, [batch_size, num_steps])

        # A deep cyclic neural network with LSTM structure and dropout structure is defined.
        dropout_keep_prob = LSTM_KEEP_PROB if is_training else 1.0
        lstm_cells = [
            tf.nn.rnn_cell.DropoutWrapper(tf.nn.rnn_cell.BasicLSTMCell(HIDDEN_SIZE), output_keep_prob=dropout_keep_prob)
            for _ in range(NUM_LAYERS)
        ]
        cell = tf.nn.rnn_cell.MultiRNNCell(lstm_cells)

        # Initialize the nearest state, which is the vector of all zeros. This quantity is used only when each epoch initializes the first batch.
        self.initial_state = cell.zero_state(batch_size, tf.float32)

        # Defining Word Vector Matrix
        embedding = tf.get_variable("embedding", [VOCAB_SIZE, HIDDEN_SIZE])

        # Converting Input Words into Word Vectors
        inputs = tf.nn.embedding_lookup(embedding, self.input_data)

        # Use dropout only in training
        if is_training:
            inputs = tf.nn.dropout(inputs, EMBEDDING_KEEP_PROB)

        # Define the output list. Here, the output of LSTM structure at different times is collected, and then provided to the software Max layer together.
        outputs = []
        state = self.initial_state
        with tf.variable_scope("RNN"):
            for time_step in range(num_steps):
                if time_step > 0:
                    tf.get_variable_scope().reuse_variables()
                cell_output, state = cell(inputs[:, time_step, :], state)
                outputs.append(cell_output)

        # Expand the output queue into the shape of [batch, hidden_size * num_steps], and then reshape into the shape of [batch*num_steps, hidden_size].
        output = tf.reshape(tf.concat(outputs, 1), [-1, HIDDEN_SIZE])

        # Softmax Layer: Converting RNN output at each location into logits for each word
        if SHARE_EMB_AND_SOFTMAX:
            weight = tf.transpose(embedding)
        else:
            weight = tf.get_variable("weight", [HIDDEN_SIZE, VOCAB_SIZE])
        bias = tf.get_variable("bias", [VOCAB_SIZE])
        logits = tf.matmul(output, weight) + bias

        # Definition of Cross Entropy Loss Function and Average Loss
        loss = tf.nn.sparse_softmax_cross_entropy_with_logits(
            labels=tf.reshape(self.targets, [-1]),
            logits=logits
        )
        self.cost = tf.reduce_sum(loss) / batch_size
        self.final_state = state

        # Define backpropagation operations only when training models
        if not is_training:
            return

        trainable_variables = tf.trainable_variables()
        # Controlling gradient size, defining optimization methods and training steps
        grads, _ = tf.clip_by_global_norm(tf.gradients(self.cost, trainable_variables), MAX_GRAD_NORM)
        optimizer = tf.train.GradientDescentOptimizer(learning_rate=1.0)
        self.train_op = optimizer.apply_gradients(zip(grads, trainable_variables))


# Run train_op on data with the given model model and return the perplexity value on all data
def run_epoch(session, model, batches, train_op, output_log, step):
    # Auxiliary variables for calculating average perplexity
    total_costs = 0.0
    iters = 0
    state = session.run(model.initial_state)
    # Training an epoch
    for x, y in batches:
        # Run train_op on the current batch and calculate the loss value. The cross-entropy loss function calculates the probability that the next word is a given word.
        cost, state, _ = session.run(
            [model.cost, model.final_state, train_op],
            {model.input_data: x, model.targets: y, model.initial_state: state}
        )
        total_costs += cost
        iters += model.num_steps

        # Only log output during training
        if output_log and step % 100 == 0:
            print("After %d steps, perplexity is %.3f" % (step, np.exp(total_costs / iters)))

        step += 1

    # Returns the perplexity value of the given model on the given data
    return step, np.exp(total_costs / iters)


# Read data from a file and return an array containing word numbers
def read_data(file_path):
    with open(file_path, "r") as fin:
        # Read the entire document into a long string
        id_string = ' '.join([line.strip() for line in fin.readlines()])
    # Convert the read word number to an integer
    id_list = [int(w) for w in id_string.split()]
    return id_list


def make_batches(id_list, batch_size, num_step):
    # batch_size: The number of samples in a batch
    # num_batches: Number of batches
    # num_step: Sequence length of a sample
    # Calculate the total number of batches. The number of words contained in each batch is batch_size* num_step
    num_batches = (len(id_list) - 1) // (batch_size * num_step)

    # The data is organized into a two-dimensional array of dimensions [batch_size, num_batches*num_step]
    data = np.array(id_list[: num_batches * batch_size * num_step])
    data = np.reshape(data, [batch_size, num_batches * num_step])

    # Along the second dimension, the data is divided into num_batches batches and stored in an array.
    data_batches = np.split(data, num_batches, axis=1)

    # Repeat the above, but move one bit to the right at each position. Here you get the next word that RNN needs to predict for each step of output.
    label = np.array(id_list[1: num_batches * batch_size * num_step + 1])
    label = np.reshape(label, [batch_size, num_batches * num_step])
    label_batches = np.split(label, num_batches, axis=1)
    # Returns an array of num_batches in length, each of which includes a data matrix and a label matrix
    # print(len(id_list))
    # print(num_batches * batch_size * num_step)
    return list(zip(data_batches, label_batches))


def main():
    # Define initialization functions
    initializer = tf.random_uniform_initializer(-0.05, 0.05)

    # Definition of a cyclic neural network model for training
    with tf.variable_scope("language_model", reuse=None, initializer=initializer):
        train_model = PTBModel(True, TRAIN_BATCH_SIZE, TRAIN_NUM_STEP)

    # Define the cyclic neural network model for testing. It shares parameters with train_model, but does not drop out
    with tf.variable_scope("language_model", reuse=True, initializer=initializer):
        eval_model = PTBModel(False, EVAL_BATCH_SIZE, EVAL_NUM_STEP)

    # Training model
    with tf.Session() as session:
        tf.global_variables_initializer().run()
        train_batches = make_batches(read_data(TRAIN_DATA), TRAIN_BATCH_SIZE, TRAIN_NUM_STEP)
        eval_batches = make_batches(read_data(EVAL_DATA), EVAL_BATCH_SIZE, EVAL_NUM_STEP)
        test_batches = make_batches(read_data(TEST_DATA), EVAL_BATCH_SIZE, EVAL_NUM_STEP)

        step = 0
        for i in range(NUM_EPOCH):
            print("In iteration: %d" % (i + 1))
            step, train_pplx = run_epoch(session, train_model, train_batches, train_model.train_op, True, step)
            print("Epoch: %d Train Perplexity: %.3f" % (i + 1, train_pplx))

            _, eval_pplx = run_epoch(session, eval_model, eval_batches, tf.no_op(), False, 0)
            print("Epoch: %d Eval Perplexity: %.3f" % (i + 1, eval_pplx))

        _, test_pplx = run_epoch(session, eval_model, test_batches, tf.no_op(), False, 0)
        print("Test Perplexity: %.3f" % test_pplx)


if __name__ == '__main__':
    main()

Note that the four files need to be pre-processed to the directory of the current. py file before running the code.

Input results: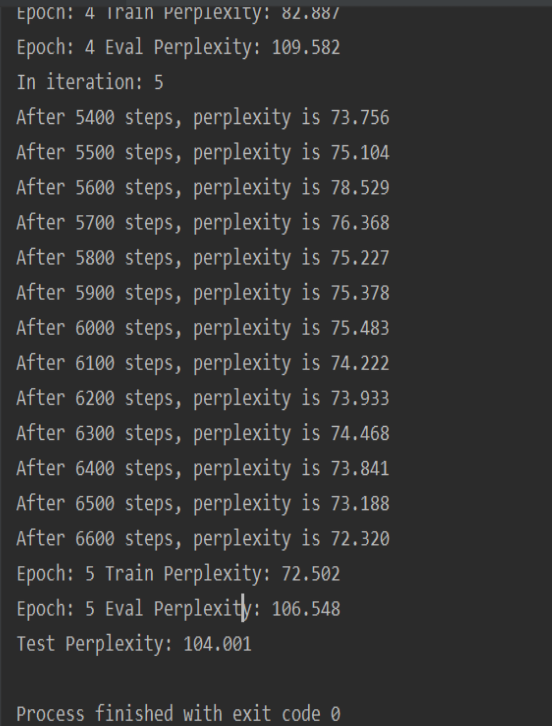

I can find that the final perplexity value is around 104. At the beginning, the perplexity value is about 10,000, which is equivalent to randomly selecting the next word from 10,000 words. After the training, the perplexity on the training data dropped to 104, indicating that through training, the range of the next word selected was reduced from 10,000 to 104. By adjusting the number and size of LSTM hidden layer nodes and the number of training rounds, perplexity can also be reduced to a lower level.