2021SC@SDUSC

Code address: similarity/f1_score.py at master · tensorflow/similarity · GitHub

import tensorflow as tf

from tensorflow_similarity.types import FloatTensor
from .classification_metric import ClassificationMetric


class F1Score(ClassificationMetric):
    """Calculates the harmonic mean of precision and recall.
    Computes the F-1 Score given the query classification counts. The metric is
    computed as follows:
    $$
    F_1 = 2 \cdot \frac{\textrm{precision} \cdot \textrm{recall}}{\textrm{precision} + \textrm{recall}}
    $$
    args:
        name: Name associated with a specific metric object, e.g.,
        f1@0.1
    Usage with `tf.similarity.models.SimilarityModel()`:
    ```python
    model.calibrate(x=query_examples,
                    y=query_labels,
                    calibration_metric='f1')
    ```
    """
    def __init__(self, name: str = 'f1') -> None:
        super().__init__(
                name=name,
                canonical_name='f1_score')

    def compute(self,
                tp: FloatTensor,
                fp: FloatTensor,
                tn: FloatTensor,
                fn: FloatTensor,
                count: int) -> FloatTensor:
        """Compute the classification metric.
        The `compute()` method supports computing the metric for a set of
        values, where each value represents the counts at a specific distance
        threshold.
        Args:
            tp: A 1D FloatTensor containing the count of True Positives at each
            distance threshold.
            fp: A 1D FloatTensor containing the count of False Positives at
            each distance threshold.
            tn: A 1D FloatTensor containing the count of True Negatives at each
            distance threshold.
            fn: A 1D FloatTensor containing the count of False Negatives at
            each distance threshold.
            count: The total number of queries
        Returns:
            A 1D FloatTensor containing the metric at each distance threshold.
        """
        recall = tf.math.divide_no_nan(tp, tp + fn)
        precision = tf.math.divide_no_nan(tp, tp + fp)
        numer = 2 * recall * precision
        denom = recall + precision
        result: FloatTensor = tf.math.divide_no_nan(numer, denom)
        return result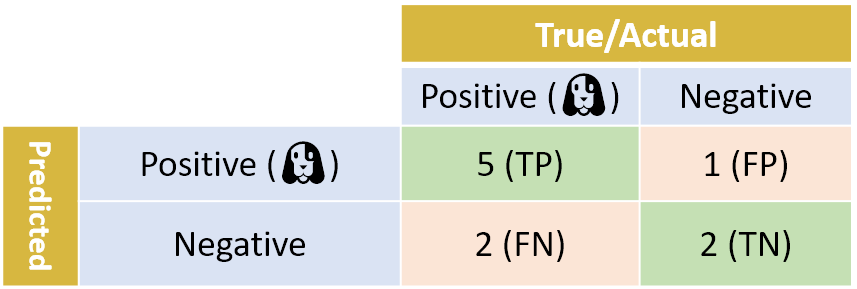

Generally speaking, we prefer classifiers with higher accuracy and recall score. However, there is a trade-off between accuracy and recall: when adjusting the classifier, increasing the accuracy score usually reduces the recall score, and vice versa - there is no free lunch.
Now suppose you have two classifiers - classifier A and classifier B - each with its own accuracy and recall. One has a better recall score and the other has better accuracy. We want to talk about their relative performance. In other words, we want to summarize the performance of the model as an indicator. This is where the F1 score is used. This is a method of combining precision and recall into one number. The F1 score is calculated using the average ("average") rather than the usual arithmetic average. It uses the harmonic average, which is given by this simple formula:
F1-score = 2 × (accuracy) × Recall rate) / (precision + recall rate)
In the above example, the F1 score of our binary classifier is:
F1-score = 2 × (83.3% × 71.4%) / (83.3% + 71.4%) = 76.9%
Similar to the arithmetic mean, the F1 score will always be between accuracy and Recall. But it behaves differently: F1 scores give lower numbers greater weight. For example, when Precision is 100% and Recall is 0%, F1 score will be 0%, not 50%. Or, for example, suppose that the accuracy of classifier A = Recall rate = 80%, the accuracy of classifier B = 60%, and the Recall rate = 100%. Arithmetically, the average values of accuracy and Recall of the two models are the same. However, when we use the harmonic average formula of F1, the score of classifier A will be 80%, while the score of classifier B will be only 75%. The low Precision score of Model B lowers its F1 score.