Loss function, back propagation

Loss function: the difference between the predicted value and the correct value.
Objective: to find a set of parameters w and b to minimize the loss function.
Gradient: the vector after the function calculates the partial derivative for each parameter. The downward direction of the function gradient is the decreasing direction of the function.
Gradient descent method: along the direction of gradient descent of loss function, find the minimum value of loss function and get the optimal parameters.

The above concepts have been touched in the high mathematics, but the despicable talents are short of learning and still don't understand.

Back propagation: from back to front, the loss function is calculated layer by layer for each neuron parameter
All parameters are updated iteratively.

Here is an example:

import tensorflow as tf

w = tf.Variable(tf.constant(5, dtype=tf.float32))
lr = 0.2
epoch = 40

for epoch in range(epoch):  # for epoch defines the top-level loop, which means to loop epoch times to the data set. In this case, the data set has only one w. when initializing, constant is assigned as 5, and the loop iterates 100 times.
    with tf.GradientTape() as tape:  # The gradient is calculated from with structure to grads frame.
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)  # The. gradient function tells who to derivative from

    w.assign_sub(lr * grads)  # . assign sub: w -= lr*grads: w = w - lr*grads
    print("After %s epoch,w is %f,loss is %f" % (epoch, w.numpy(), loss))

# lr initial value: 0.2, please see the convergence process with self-learning rate of 0.001 0.999
# The ultimate goal is to find the optimal parameter W with the least loss, that is, w = -1

The results of running in Anaconda are as follows:

After 40 iterations, the minimum w value of loss function is found.

tensor

Here is a brief summary:
The 0-D tensor to the 2-D tensor are the scalar, vector and matrix that we are familiar with, and the corresponding order is 0, 1 and 2. 3-dimensional and higher-order tensors are called n-order tensors.

import tensorflow as tf

a = tf.constant([1, 5], dtype=tf.int64)
print("a:", a)
print("a.dtype:", a.dtype)
print("a.shape:", a.shape)

# Native default tf.int32 can remove dtype try to check the default value

Create a one-dimensional tensor

import tensorflow as tf

a = tf.constant([1, 5], dtype=tf.int64)
print("a:", a)
print("a.dtype:", a.dtype)
print("a.shape:", a.shape)

# Native default tf.int32 can remove dtype try to check the default value

output

If [1,5] in the code is changed to 1, then the tensor of order 0 is created, and it is changed to [1,2], [2,5] is two-dimensional.

The three-dimensional tensor is shown in the figure:
The shape value is (2, 2, 1). The first 2 indicates that the first dimension has two elements, the second 2 indicates that the second dimension has two elements, and the first 1 indicates that the third dimension has one element.

numpy data type converted to TensorFlow data type

import tensorflow as tf
import numpy as np

a = np.arange(0, 5)
b = tf.convert_to_tensor(a, dtype=tf.int64)
print("a:", a)
print("b:", b)

Output:

Create a special tensor

a = tf.zeros([2, 3])
b = tf.ones(4)
c = tf.fill([2, 2], 9)
print("a:", a)
print("b:", b)
print("c:", c)

Output:

The parameters in parentheses of the above three methods are dimensions:
Number of one-dimensional direct writes
Two dimensional use [row, column]
Multidimensional use [n,m,j ]
For example: create a one-dimensional tensor a = tf.zero (4)

Generate the random number of normal distribution, the default mean value is 0, and the standard deviation is 1. tf. random.normal (dimension, mean = mean, stddev = standard deviation)
r generates tf. random.truncated normal (dimension, mean = mean, stddev = standard deviation)

d = tf.random.normal([2, 2], mean=0.5, stddev=1)
print("d:", d)
e = tf.random.truncated_normal([2, 2], mean=0.5, stddev=1)
print("e:", e)

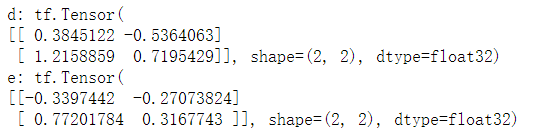
Generate uniformly distributed random number [minval, maxval)
TF. Random. Uniform (dimension, minval = minimum, maxval = maximum)

f= tf.random.uniform([2, 2], minval=0, maxval=1)
print(f)

Output: