meaning of the title

Give some points, find four points, ask one point in the triangle surrounded by the remaining three points, and ask the number of solutions.

Title Solution

It makes me feel like I don't want to touch geometry...
Fantastic, fantastic in accuracy, fantastic in different expressions of the same meaning, clear and concise thinking, why write so many special cases (vi)
Cried

Enumerate each point as the point inside the triangle and see how many triangles can enclose it.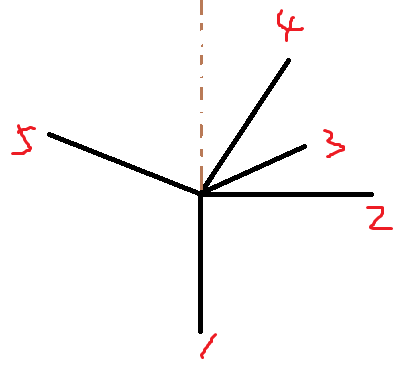

No. 1 energy and (4,5) (3,5) (2,5) composition
Obviously, the angle between two points outside No. 1 should not be greater than 180 (turn counterclockwise).
So, we need to figure out how many points there are within 180 degrees counter-clockwise for each point.
f[i]f[i]f[i] f [i] denotes the above functions
Points within 180 degrees of 1 have 2, 3, 4
Is the answer f [2] + F [3] + F [4] f [2] + F [3] + F [4] f [2] + F [4] f [2] + F [3] + F [4]?
No, we need to delete a part.
Observations show that the other two points must be located on both sides of 1, so
f[4]f[4]f[4] f [4] is the answer
f[3]f[3]f[3] f [3] less than 4
f[2]f[2]f[2] f [2] less 4, 3
Obviously, the undercounted number is a sequence of equal-difference numbers such as 0,1,2...n_10,1,2...n_1, so this part can be obtained by knowing that O(1)O(1)O(1)O(1)O(1) after f[] f[~]f[]
Is that all?
No.
The points found to be collinear with 1 and on the opposite side are not counted, but will be counted.
So the number of points on the opposite side of the line is required to be multiplied by f[1]f[1]f[1], which is the number to be reduced. Do you?
No
Because f [] f[~]f [] contains points that are collinear with and on the same side, there is no need to subtract, because it is not legal to add the number before.
To sum up, we need to calculate
The number of counterclockwise 0 degree points, counterclockwise more than 0 points less than 180 degrees, counterclockwise 180 degrees points...

Tomb Tomb Tomb Tomb Tomb Tomb Tomb Tomb Tomb Tomb Tomb Tomb. (((m--)m)

Code

#include<bits/stdc++.h>
#define N 2010
#define INF 0x3f3f3f3f
#define eps 1e-6
#define pi 3.141592653589793
#define mod 998244353
#define P 1000000007
#define LL long long
#define pb push_back
#define fi first
#define se second
#define cl clear
#define si size
#define lb lower_bound
#define ub upper_bound
#define bug(x) cerr<<#x<<"      :   "<<x<<endl
#define mem(x) memset(x,0,sizeof x)
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)  
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
using namespace std;
int dcmp(double x){if (fabs(x)<eps)return 0;else return x<0?-1:1;}
struct Point
{
    LL x,y;
    bool operator < (const Point &a)const
    {return (x-a.x)<0 || ((x-a.x)==0 && (y-a.y)<0);}
    Point(LL x=0,LL y=0):x(x),y(y){ }
}a[N],c[N];
typedef Point Vector;
  
Vector operator + (Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
Vector operator - (Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
Vector operator * (Vector a,LL b){return Vector(a.x*b,a.y*b);}
bool operator == (Vector a,Vector b){return (a.x-b.x)==0 && (a.y-b.y)==0;}
inline LL Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;} //Cross product
inline LL Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}  //Dot product
inline double Length(Vector a){return sqrt(Dot(a,a));}
inline double Angle(Vector a,Vector b){return acos(min(1.0,max(-1.0,Dot(a,b)/Length(a)/Length(b))));}
bool cmp(Point a,Point b){
    if(a.y<0 && b.y>=0 || a.y>=0 && b.y<0) return a.y>=0;
    if(a.y*b.y==0)
    {
        if(a.y==0 && b.y==0) return a.x>b.x;
        return Cross(a,b)>0;
    }
    return Cross(a,b)>0;
}
 
LL ans=0;
int cnt;
int v[N<<1],d[N<<1],p[N],w[N];
 
//From a counter-clockwise rotation to b rotation angle, range [0,360]
double GetAngle(Vector a,Vector b)
{
    double x=Angle(a,b),y=Cross(a,b);
    if (dcmp(y)<0)x=pi*2-x;
    return x;
}
 
void slove(){
    sort(c,c+cnt,cmp);
 
    if (dcmp(GetAngle(c[0],c[cnt-1])-pi)<=0) return;
    for(int i=0;i<cnt-1;i++)
        if (dcmp(GetAngle(c[i],c[i+1])-pi)>=0) return;
 
 
    for(int i=0;i<cnt;i++) c[i+cnt]=c[i];
  
    int k=0,ka=0,kb=0,m=cnt<<1;
    
    for(int i=0;i<cnt;i++){
        k=max(k,i);ka=max(ka,i);kb=max(kb,i);
 
        while(k<m&&(dcmp(GetAngle(c[i],c[k+1]))==0||Cross(c[i],c[k+1])>0)) k++;
        v[i]=v[i+cnt]=k-i;
 
        while(ka<m&&Cross(c[i],c[ka+1])>=0) ka++;
        w[i]=ka-k;
 
        while(kb<m&&Cross(c[i],c[kb+1])==0&&Dot(c[i],c[kb+1])>0) kb++;
        p[i]=kb-i;
 
    }
  
    d[0]=v[0]; for(int i=1;i<m;i++) d[i]=d[i-1]+v[i];
    for(int i=0;i<cnt;i++){
 
        int sz=v[i]-p[i];
 
        int t=(d[i+v[i]]-d[i+p[i]])-sz*(sz-1)/2-sz*w[i];
 
        ans+=t;
 
    }
}
  
int main(int argc, char const *argv[])
{
 
    int n;
    sc(n);
    for(int i=0;i<n;i++) scanf("%lld%lld",&a[i].x,&a[i].y);
    for(int i=0;i<n;i++){
        cnt=0;
        for(int j=0;j<n;j++) if (i^j) c[cnt++]=a[j]-a[i];
        slove();
    }
    cout<<ans/3;
    return 0;
}