The problem of finding the intersection of ring and acyclic single linked list is one of the top two problems in the linked list type problem, and listen to it all.
1, Title Description
Given two single linked lists that may or may not have rings, the head nodes head1 and head2.
Please implement a function. If two linked lists intersect, please return the first node of the intersection. If it does not intersect, null is returned
Requirements: if the sum of the lengths of the two linked lists is N, the time complexity should reach O(N) and the additional space complexity should reach O(1).
2, Train of thought
The solution is divided into two steps:
(1) Find the ring in node of the single linked list, and return null if there is no ring
(2) According to the entry node of the linked list, we will discuss it again
1. Find the ring in node of the single linked list, and return null if there is no ring
(1) Traverse the single linked list. If the traversed node is null, the single linked list must be acyclic
(2) Otherwise there is a ring
Prepare a fast pointer and a slow pointer. At the beginning, both pointers start from the first node. The fast pointer walks two nodes at a time and the slow pointer walks one node at a time until the two pointers meet.
At this time, the fast pointer starts from the node again, one node at a time; The slow pointer continues to go down from the meeting place, still one node at a time. When the two pointers meet again, the node is the ring entry node.
2. According to the entry node of the linked list, we will discuss it again
(1) Both linked lists are acyclic
Traverse one of the linked lists and record the length length1 of the linked list and the last node end1; Traverse another linked list and record the length of the linked list length2 and the last node end2.
If end1 and end2 are not equal, the two linked lists must not intersect; Otherwise, calculate the difference a between length1 and length2. The long linked list goes a node first, and then the two linked lists go down one by one. The first equal node is the first node of intersection.
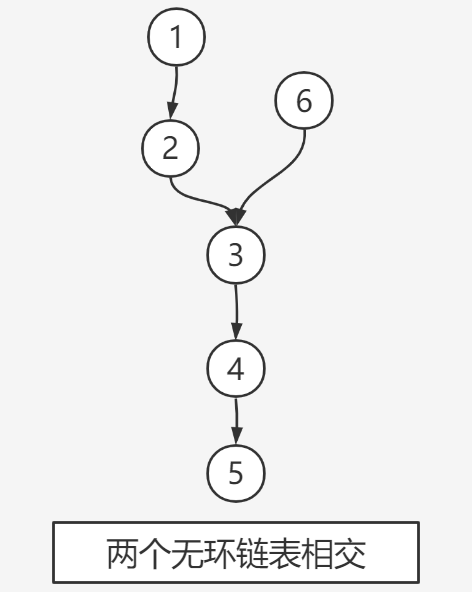
(2) One has a ring and one has no ring
In this case, two linked lists cannot intersect. (everyone can try to make up such a structure. Remember, it's a single linked list)
(3) Both linked lists have rings
In three cases, each has a ring but does not intersect; The loop entry node is the same; There are two loop nodes.
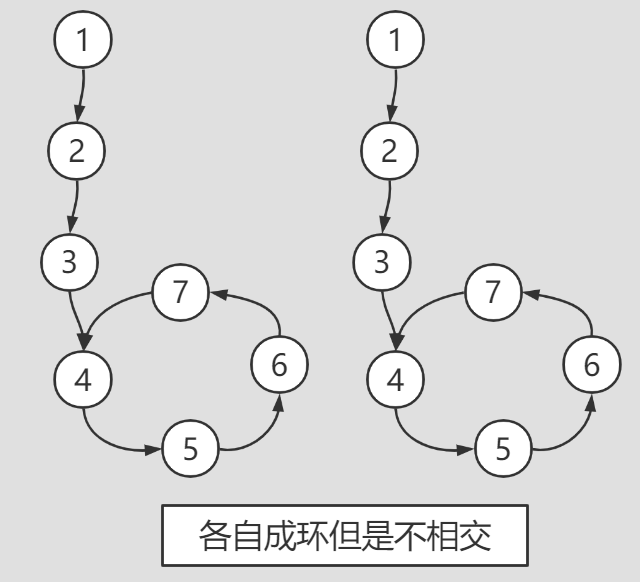
1) Each has a ring but does not intersect
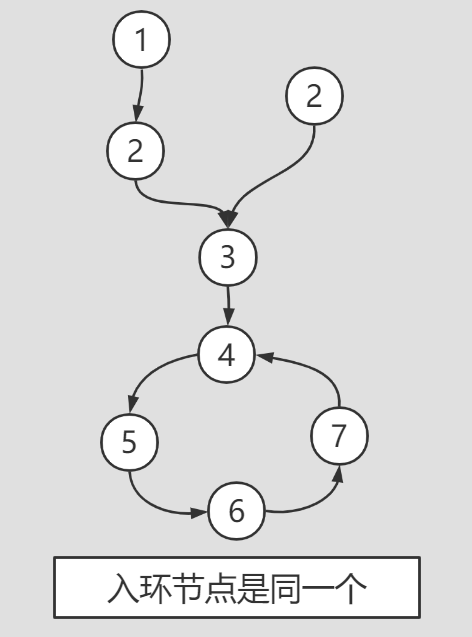
2) The ring in node is the same
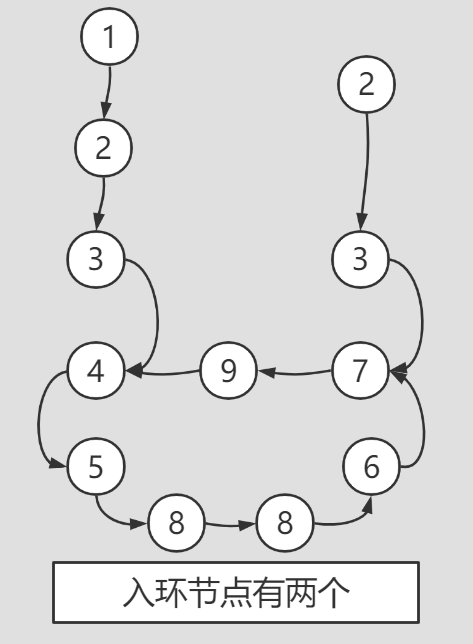
3) There are two loop nodes
The ring nodes of the two linked lists are equal: that is, the ring nodes are the same. In this case, the solution process is the same as the process in which the two linked lists are acyclic and intersecting, that is, the following rings can be ignored in the solution.
The ring entry nodes of the two linked lists are not equal: the first race or the third race. At this time, start from one of the ring entry nodes and traverse a circle. If you encounter the second ring entry node when returning to yourself, it is the third race, otherwise it is the first race.
3, Detailed reference code
1. Find the looping node of the single linked list
/**
* Find the ring in node of the single linked list, and return null if there is no ring
*
* @author Java And algorithm learning: Monday
*/
public static Node getLoopNode(Node head) {
if (head == null || head.next == null || head.next.next == null) {
return null;
}
//Quick pointer
Node fast = head.next.next;
//Slow pointer
Node slow = head.next;
while (fast != slow) {
//If a fast pointer becomes empty while walking, the single linked list must be acyclic
if (fast.next == null || fast.next.next == null) {
return null;
}
fast = fast.next.next;
slow = slow.next;
}
//When the fast and slow pointers meet, the fast pointer starts from the node again
fast = head;
while (fast != slow) {
//At this time, it is no longer necessary to judge that it is empty. If you can go here, the single linked list must be ring
//At this time, the fast pointer walks one node at a time
fast = fast.next;
//The slow pointer still walks one node at a time
slow = slow.next;
}
return slow;
}
2. According to the entry node of the linked list, we will discuss it again
(1) Both linked lists are acyclic
/**
* Now that you know that the two linked lists are acyclic, find their first intersection node
*
* @author Java And algorithm learning: Monday
*/
public static Node noLoop(Node head1, Node head2) {
if (head1 == null || head2 == null) {
return null;
}
Node current1 = head1;
Node current2 = head2;
int n = 0;
//The linked list is traversed once to get the length and the last node
while (current1.next != null) {
n++;
current1 = current1.next;
}
//The linked list is traversed twice to get the length difference and the last node
while (current2.next != null) {
n--;
current2 = current2.next;
}
//If the last node of two linked lists is not equal, it must not intersect
if (current1 != current2) {
return null;
}
//The head node of the long linked list is given to current1
current1 = n > 0 ? head1 : head2;
//The head node of the short linked list is given to current2
current2 = current1 == head1 ? head2 : head1;
n = Math.abs(n);
//The long linked list has n nodes first
while (n != 0) {
n--;
current1 = current1.next;
}
//Two linked lists go down one by one. The first equal node is the first intersecting node
while (current1 != current2) {
current1 = current1.next;
current2 = current2.next;
}
return current1;
}
(3) Both linked lists have rings
/**
* Both linked lists have rings
* In three cases, each has a ring but does not intersect; The loop entry node is the same; There are two loop nodes
*
* @author Java And algorithm learning: Monday
*/
public static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {
Node current1 = null;
Node current2 = null;
if (loop1 == loop2) {
current1 = head1;
current2 = head2;
int n = 0;
//Calculate the number of nodes in the head1 linked list
while (current1 != loop1) {
n++;
current1 = current1.next;
}
//Calculate the difference between the number of nodes in two linked lists
while (current2 != loop2) {
n--;
current2 = current2.next;
}
//The head node of the long linked list is given to current1
current1 = n > 0 ? head1 : head2;
//The head node of the short linked list is given to current2
current2 = current1 == head1 ? head2 : head1;
n = Math.abs(n);
//The long linked list has n nodes first
while (n != 0) {
current1 = current1.next;
n--;
}
//Two linked lists go down one by one. The first equal node is the first intersecting node
while (current1 != current2) {
current1 = current1.next;
current2 = current2.next;
}
return current1;
} else {
//If the entry nodes of two linked lists are not equal, they have rings but do not intersect, or there are two entry nodes
current1 = loop1.next;
//Start from one of the ring entry nodes and traverse a circle. If you encounter the second ring entry node when you return to yourself, there are two ring entry nodes
while (current1 != loop1) {
if (current1 == loop2) {
//At this time, the two loop in nodes are the first intersection node. Just return one of them
return loop1;
}
current1 = current1.next;
}
return null;
}
}
The above is the core detailed reference code. I believe that the main method and test method can be easily written. Of course, I want to refer to all the codes. The Github address of all the codes in this article is also attached here: