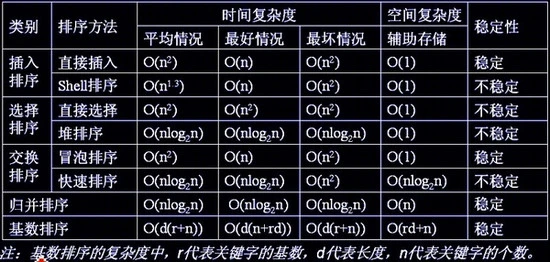
This paper will take you to understand the common sorting algorithms in the form of speaking + moving graph, briefly analyze the complexity, stability and other indicators, and give the reference code. Finally, the use of Amway sort() function.

Select sort

The smallest element after each selection is placed in front.

• Time complexity O ( n 2 ) O(n^2) O(n2)
• Stability: unstable
  For example, 2 2 1, after selecting the smallest 1 in the first pass, 1 2 2 is obtained by exchange, and the relative position of the two 2 changes.

Stability: that is, whether the relative position of the elements with the same (keyword / element value) changes after sorting.

• Whether the number of sorting passes is related to the original sequence: irrelevant
  No matter the ascending order is out of order, the selected sorting must traverse to the last element every time to ensure that the selected element is the smallest.

#include<bits/stdc++.h>
using namespace std;
void selection(int a[],int n){
	for(int i=0;i<n;i++){
		int min=i;  //Record minimum element
		for(int j=i+1;j<n;j++){  //Find the smallest element after
			if(a[j]<a[min])
				min=j;
		}
		swap(a[i],a[min]);  //exchange
	}
}
int main(){
	int a[5]={3,5,1,4,2};
	selection(a,5);
	for(int i=0;i<5;i++)cout<<a[i]<<" "; 
	return 0;
}

Bubble sorting

Compare two adjacent elements from front to back. If the former > the latter, exchange them. Elements come back like bubbles.

• Time complexity O ( n 2 ) O(n^2) O(n2)

• Stability: stable
  When the same or larger elements are encountered, they are not exchanged.

• Whether the number of sorting passes is related to the original sequence:
  Under the extreme conditions of ascending order, you can record whether the exchange occurs. If there is no exchange, the sequence is orderly and you can exit.

#include<bits/stdc++.h>
using namespace std;
void bubble(int a[],int n){
	for(int i=0;i<n;i++){
		bool tag=false;  //Record whether exchange occurs in this trip
		for(int j=0;j<n-i-1;j++){
			if(a[j]>a[j+1]){  //Compare with the latter element
				swap(a[j],a[j+1]);
				tag=true;
				}
			}
		if(tag==false)break;  //No exchange, exit
	}
}
int main(){
	int a[5]={3,5,1,4,2};
	bubble(a,5);
	for(int i=0;i<5;i++)cout<<a[i]<<" "; 
	return 0;
}

Insert sort

Each time the elements to be sorted are correctly inserted into the previously ordered sequence, just like playing cards.

• Time complexity O ( n 2 ) O(n^2) O(n2)

• Stability: stable
  Compare and then move from back to front. If you encounter the same, you will not exchange.

• Whether the number of sorting passes is related to the original sequence: irrelevant
  Insert 1 element per trip and fix n-1 trips.

#include<bits/stdc++.h>
using namespace std;
void insertion(int a[],int n){
	for(int i=0;i<n;i++){  //Traverse i elements to be inserted
		for(int j=i;j>0;j--){  //Insert front
			if(a[j]<a[j-1])
				swap(a[j],a[j-1]);
		}
	}
}
int main(){
	int a[5]={3,5,1,4,2};
	insertion(a,5);
	for(int i=0;i<5;i++)cout<<a[i]<<" "; 
	return 0;
}

Shell Sort

Each time, the elements separated by X (increment) are divided into a sub table for direct insertion sorting (regardless of other elements), and then x is continuously reduced. From basic order to overall order.

• Time complexity O ( n 2 ) O(n^2) O(n2)
• Stability: unstable
  When the same elements are divided into different sub tables, their relative positions may be changed.
• Whether the number of sorting passes is related to the original sequence: irrelevant
  Regardless of the original sequence state, it is only related to increment x (i.e. array size n).

#include<bits/stdc++.h>
using namespace std;
void shell(int a[],int n){
	for(int x=n/2;x>0;x/=2){  //Increment x 
		for(int i=x;i<n;i++){  //Partition sub table 
			//Insert sort in sub table 
			for(int j=i;j>=x&&a[j]<a[j-x];j-=x) 
				swap(a[j],a[j-x]);
		}
	}
}
int main(){
	int a[5]={3,5,1,4,2};
	shell(a,5);
	for(int i=0;i<5;i++)cout<<a[i]<<" "; 
	return 0;
}

Quick sort

Each time, put the larger one on its right and the smaller one on its left, then the position of the element is determined, and then sort other elements recursively.

• Time complexity O ( n l o g n ) O(nlogn) O(nlogn)
  Need to determine n n The correct position of n numbers, the left and right half intervals are compared once per trip, and the complexity is O ( l o g n ) O(logn) O(logn).

• Stability: unstable
  The relative position will be changed when the numbers on the left and right sides are exchanged.

• Whether the number of sorting passes is related to the original sequence:

#include<bits/stdc++.h>
using namespace std;
int partition(int a[],int low,int high){  //One trip Division
	int cur=a[low];  //The value of the current element  
	while(low<high){
		while(low<high&&a[high]>=cur)high--;  //Find an element smaller than the current value from back to front
		a[low]=a[high];  //Change the small one to the front
		while(low<high&&a[low]<=cur)low++;  //Look from front to back for elements larger than the current value
		a[high]=a[low];  //Change the big one to the back
	}
	//When low=high, jump out of the loop, and this position is the correct position of the current element
	a[low]=cur;  
	return low;
}
void qsort(int a[],int low,int high){
	if(low<high){
		int idx=partition(a,low,high);  //Determine the correct location of the element
		qsort(a,low,idx-1);  //Recursive left and right intervals
		qsort(a,idx+1,high);
	}
}
int main(){
	int a[5]={3,5,1,4,2};
	qsort(a,0,4);
	for(int i=0;i<5;i++)cout<<a[i]<<" "; 
	return 0;
}

(insert anti climbing information) CSDN address of blogger: https://wzlodq.blog.csdn.net/

Heap sort

Take the large root heap as an example, that is, the root element is the largest. Initially, it is disordered. From bottom to top (leaf node to root), exchange the element with a larger value in the two leaf nodes with its parent node. After the parent node is replaced, if there are child nodes (i.e. except the last layer), it is necessary to compare whether it is larger than the current two leaf nodes. Otherwise, select a larger leaf node and replace it and recurse in turn.

• Time complexity O ( n l o g n ) O(nlogn) O(nlogn)
  n − 1 n-1 n − 1 downward adjustment operation, and the complexity of each adjustment is O ( h ) O(h) O(h), i.e O ( l o g n ) O(logn) O(logn).
• Stability: unstable
  You may adjust the same keywords in the back to the front.
• Whether the number of sorting passes is related to the original sequence:
  If ordered, the complexity of each downward adjustment is O ( 1 ) O(1) O(1).

#include<bits/stdc++.h>
using namespace std;
void adjustheap(int a[], int i, int n){
    for(int j=i*2+1;j<n;){
        if(j+1<n&&a[j]<a[j+1])  //Take the older of the left and right children 
    		j++;
        if(a[i]>a[j])break;
        swap(a[i], a[j]);
        //Recursive comparison with child node size after exchange 
        i=j;
        j=2*i+1;
    }
}
void makeheap(int a[], int n){  //Build pile 
    for(int i=n/2-1; i>=0; i--)//Recursively adjusts the heap from the last parent node
        adjustheap(a,i,n);
}
void heapsort(int a[], int n){
    makeheap(a, n);
    for(int i=n-1; i>=0; i--){
        swap(a[i], a[0]);
        adjustheap(a, 0, i);
    }
}
int main(){
	int a[5]={3,5,1,4,2};
	heapsort(a,5);
	for(int i=0;i<5;i++)cout<<a[i]<<" "; 
	return 0;
}

Merge sort

Recursively divide the molecular interval until an element, and then merge the sub intervals in turn. At this time, the interior of each sub interval is orderly. The merging process is to compare the first element of two sub intervals and take the smallest one until one sub interval is taken, and then directly add the remaining elements of another sub interval.

• Time complexity O ( n l o g n ) O(nlogn) O(nlogn)
  Merge every time O ( n ) O(n) O(n), total required O ( l o g n ) O(logn) O(logn) merge.
• Stability: stable
  The merge operation merges two sub intervals from front to back without changing the relative position.
• Whether the number of sorting passes is related to the original sequence: irrelevant
  Regardless of the original sequence state, it should be divided into an element and then merged.

#include<bits/stdc++.h>
using namespace std;
int b[5];  //Auxiliary array 
void merge(int a[],int low,int mid,int high){
	for(int k=low;k<=high;k++)b[k]=a[k];
	int i=low,j=mid+1,k=low;
	//i. J represents the subscript of the front element of the left and right sub intervals respectively
	//k represents the subscript of the merged array 
	while(i<=mid&&j<=high){
		if(b[i]<=b[j])
			a[k++]=b[i++];
		else a[k++]=b[j++];
	}
	while(i<=mid)a[k++]=b[i++];
	while(j<=high)a[k++]=b[j++]; 
}
void mergeSort(int a[],int low,int high){
	if(low<high){
		int mid=(low+high)/2;  //Divide the interval from the middle
		mergeSort(a,low,mid);  //Merge the left and right sections respectively 
		mergeSort(a,mid+1,high); 
		merge(a,low,mid,high);  //Merge 
	}
}
int main(){
	int a[5]={3,5,1,4,2};
	mergeSort(a,0,4);
	for(int i=0;i<5;i++)cout<<a[i]<<" "; 
	return 0;
}

Cardinality sort

Traverse from the low bit to the high bit of each number. The second cycle traverses each number, queue up to the corresponding bits (0 ~ 9) according to the value of this bit, and finally take out these numbers from 9 to 0 in the order of addition, so as to complete the sorting of the i-th bit by one trip of data.

• Time complexity O ( d ( n + r ) ) O(d(n+r)) O(d(n+r))
  r r r represents the cardinality, d d d is the length, n n n represents the number.

• Stability: stable
  Use queues to ensure stability.

• Whether the number of sorting passes is related to the original sequence: irrelevant
  Operate according to the number of digits and elements, which is independent of the initial test state of the sequence.

• Summary

algorithm	Time complexity	stability	Is the number of sorting times related to the original sequence
Select sort	O ( n 2 ) O(n^2) O(n2)	instable	irrelevant
Bubble sorting	O ( n 2 ) O(n^2) O(n2)	stable	of
Insert sort	O ( n 2 ) O(n^2) O(n2)	stable	irrelevant
Shell Sort	O ( n 2 ) O(n^2) O(n2)	instable	irrelevant
Quick sort	O ( n l o g n ) O(nlogn) O(nlogn)	instable	of
Heap sort	O ( n l o g n ) O(nlogn) O(nlogn)	instable	of
Merge sort	O ( n l o g n ) O(nlogn) O(nlogn)	stable	irrelevant
Cardinality sort	O ( d ( n + r ) ) O(d(n+r)) O(d(n+r))	stable	irrelevant

sort()

In terms of actual programming, there is no sorting problem that sort() can't solve (if there is, there is). Its bottom layer is mainly quick sorting. The source code is no longer studied deeply. The following mainly introduces the usage of sort().
The header file is < algorithm >

#include<bits/stdc++.h>
using namespace std;
int main(){
	int a[5]={3,5,1,4,2};
	sort(a,a+5);  //The two parameters are start position and end position 
	for(int i=0;i<5;i++)cout<<a[i]<<" "; 
	return 0;
}

Well, yes, it's that simple and rough.
The following describes the complex sorting of user-defined structures.

#include<bits/stdc++.h>
using namespace std;
struct node{
	string name;
	int grade;
	node(){}
	node(string a,int b){
		name=a;
		grade=b;
	}
	bool operator<(const node&a)const{  //You can customize the less than operator 
		if(grade==a.grade)  //Same grades, names in ascending order 
			return name<a.name;
		return a.grade<grade;  //Otherwise, the score will be in descending order 
	}
}a[5]; 
bool cmp(node a,node b){  //You can also define comparison functions 
	if(a.name==b.name)  //The names are the same, and the grades are in descending order 
		return a.grade>b.grade;
	return a.name<b.name;  //Otherwise, the names are in ascending order 
} 
int main(){
	a[0]=node("c",90);
	a[1]=node("b",90);
	a[2]=node("b",95);
	a[3]=node("a",80);
	a[4]=node("da",100);
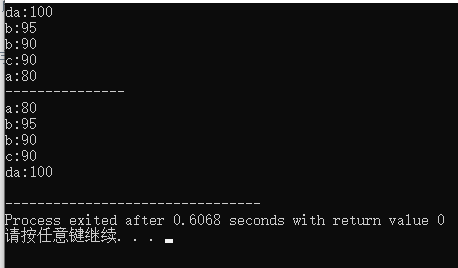
	sort(a,a+5);  //Use structure definition<
	for(int i=0;i<5;i++)
		cout<<a[i].name<<":"<<a[i].grade<<"\n"; 
	cout<<"---------------\n"; 
	sort(a,a+5,cmp);  //Using custom comparison functions
	for(int i=0;i<5;i++)
		cout<<a[i].name<<":"<<a[i].grade<<"\n"; 
	return 0;
}

Similarly, you can sort vector < >:

#include<bits/stdc++.h>
using namespace std;
struct node{
	string name;
	int grade;
	node(){}
	node(string a,int b){
		name=a;
		grade=b;
	}
	bool operator<(const node&a)const{  //You can customize the less than operator 
		if(grade==a.grade)  //Same grades, names in ascending order 
			return name<a.name;
		return a.grade<grade;  //Otherwise, the score will be in descending order 
	}
}a[5]; 
bool cmp(node a,node b){  //You can also define comparison functions 
	if(a.name==b.name)  //The names are the same, and the grades are in descending order 
		return a.grade>b.grade;
	return a.name<b.name;  //Otherwise, the names are in ascending order 
} 
int main(){
	a[0]=node("c",90);
	a[1]=node("b",90);
	a[2]=node("b",95);
	a[3]=node("a",80);
	a[4]=node("da",100);
	vector<node>v;
	for(int i=0;i<5;i++)v.push_back(a[i]);
	sort(v.begin(),v.end());  //Start position, end position, [comparison function] 
	for(int i=0;i<5;i++)
		cout<<v[i].name<<":"<<v[i].grade<<"\n"; 
	cout<<"---------------\n"; 
	sort(v.begin(),v.end(),cmp);  //Change soup without dressing 
	for(int i=0;i<5;i++)
		cout<<v[i].name<<":"<<v[i].grade<<"\n"; 
	return 0;
}

Attachment: algorithm visualization website
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

Original is not easy, please do not reprint (this is not rich, the number of visits is even worse)
Blogger homepage: https://wzlodq.blog.csdn.net/
Here we are. Don't you comment 👀
If the article is helpful to you, remember to click three times ❤