Words written before:
Sword finger offer brushes the questions for the second time. I hope each question can last for seconds. Record your understanding of the topic from the back to the front.

Nearest common ancestor of binary tree

Problem description

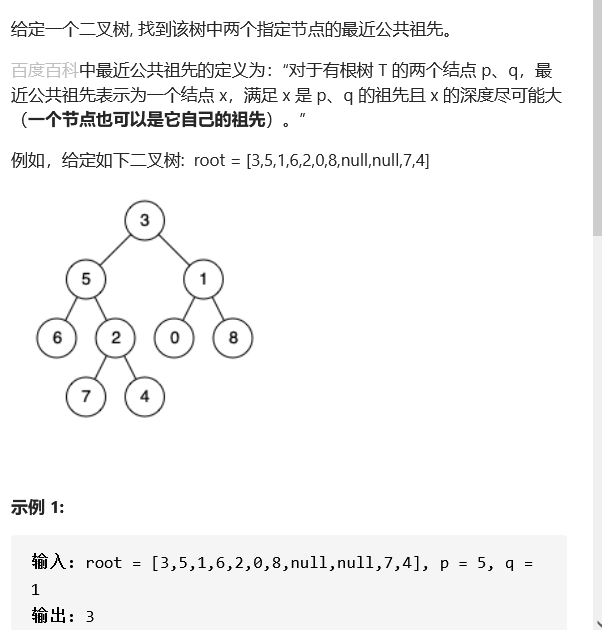
problem analysis

1. Nearest common ancestor: according to the definition of encyclopedia, there are several situations of nearest common ancestors: 1. p.q has a common ancestor and the ancestor is not themselves. 2. The ancestor is p or q itself. 3 p. q no common ancestor
2. Traversal mode: if the depth of x is required to be as large as possible, then post order traversal is required. The nearest ancestor is the one with the greatest depth Postorder traversal is the state (return value) of the root node, which needs to be determined by the left and right subtrees
3. How to handle: recursion. Three elements of recursion: termination condition, return value and what to do with this recursion. In addition, recursion can be considered that the node has been calculated at this time, and the value after recursion can be directly used for simulation.
4. Algorithm steps: 1 The subsequent traversal starts from the root node to the leftmost node, and then starts to access. If the current node is empty, it will naturally return to the current node. At the same time, if the current node = = one of qorp, the node must be the common ancestor itself. Otherwise, it can only be left and right children, so it is impossible for the current node = porq. 2. At this time, we should clarify the return value and what to do with this recursion in combination with the three elements of recursion. First, we must traverse the left and right children to find the specified node, and know the return value tree node itself in combination with the topic itself. 3. If the left and right children of the return value exist, it means that the left child may be p, the right child may be q, or the left child may be q, and the child may be p. however, in general, the node returned recursively must exist, and at this time, the specified node and the nearest common ancestor 3 + of the specified node have been found If one of the recursively returned nodes is empty, it means that the specified two nodes must be on the adjacent sibling tree. Directly return the first node of the sibling tree, that is, the other of the current recursively returned value.

Code representation

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //Trees can generally be solved recursively, but it is necessary to determine which traversal method to use
        if(root==nullptr)return root;
        if(root==q||root==p)return root;
        TreeNode*l=lowestCommonAncestor(root->left,p,q);
        TreeNode*r=lowestCommonAncestor(root->right,p,q);
        if(l==p&&r==q||l==q&&r==p)return root;
        if(r==nullptr)return l;
        if(l==nullptr)return r;
        return nullptr;
    }
};

Nearest common ancestor of binary search tree

Problem description

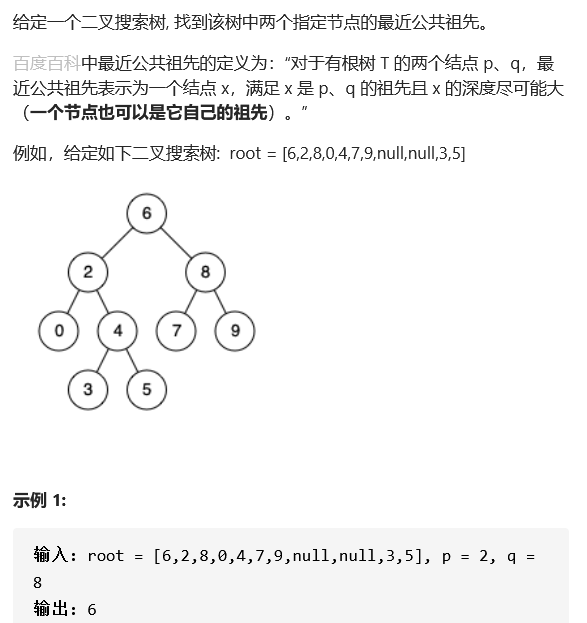
problem analysis

1. Binary search tree: the value of all nodes in the left subtree is less than that of its parent node, and the value of all nodes in the right subtree is greater than that of its parent node. Therefore, traversing the binary search tree in order is also orderly.
2. Nearest common ancestor problem: like the nearest common ancestor of binary tree, there are several points: 1. p.q has a common ancestor and the ancestor is not themselves. 2. The ancestor is p or q itself. 3 p. q no common ancestor. Combined with the characteristics of binary search tree, if p.q has a common ancestor and the ancestor is not themselves, it must be that the current node value is between the specified two nodes. If the ancestor is p or q itself, it must be that the current node is equal to one of the specified nodes. In this way, the current node is a bifurcation point and the specified node is either in the subtree, Either one of the specified nodes is the current node.
3. Dichotomy: if the specified nodes are larger than the current node, it must be found in the right subtree of the current node. If the specified nodes are smaller than the current node, it must be found in the left subtree. If this condition is not met, it means that the current node must be a bifurcation point. Just return to the current node directly, because the current node is the nearest public ancestor.

Code representation

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==NULL)return root;
        if(p->val<root->val&&q->val<root->val){
            return lowestCommonAncestor(root->left,p,q);
        }
        if(p->val>root->val&&q->val>root->val){
            return lowestCommonAncestor(root->right,p,q);
        }
        return root;
    }
};

reference resources: leetcode