Make up the number of steamed stuffed buns

[Title Description]

Xiao Ming eats breakfast at a steamed stuffed bun shop almost every morning. He found that the steamed stuffed bun shop had N Steamer, of which i This kind of steamer can just put Ai A steamed stuffed bun. Each kind of steamer has many steamers, which can be regarded as infinite steamers.
Whenever a customer wants to buy X A steamed stuffed bun, the uncle who sells steamed stuffed buns will quickly select several cages of steamed stuffed buns, so that there are just a total of them in these cages X A steamed stuffed bun. For example, there are three kinds of steamers, which can put 3, 4 and 5 steamed buns respectively. When customers want to buy 11 steamed stuffed buns, uncle will choose 2 cages of 3 and 1 cage of 5 (or 1 cage of 3 and 2 cages of 4).
Of course, sometimes uncle baozi can't figure out the quantity customers want to buy anyway. For example, there are three kinds of steamers, which can put 4, 5 and 6 steamed buns respectively. When customers want to buy seven steamed stuffed buns, uncle can't come up with it.
Xiao Ming wants to know how many kinds of numbers are there that uncle baozi can't figure out.

input
----
The first line contains an integer N. (1 <= N <= 100)
following N Each row contains an integer Ai. (1 <= Ai <= 100)  

output
----
An integer represents the answer. If there are infinite numbers that cannot be rounded up, output INF. 

For example,
Input:
2  
4  
5   

The program should output:
6  

Another example is,
Input:
2  
4  
6    

The program should output:
INF

Example explanation:
For example 1, the number that cannot be rounded up includes: 1, 2, 3, 6, 7, 11.   
For example 2, none of the odd numbers can be summed up, so there are infinite numbers.  



Resource agreement:
Peak memory consumption (including virtual machine) < 256M
CPU consume  < 1000ms


Please output in strict accordance with the requirements, and do not print like "please input"..." Superfluous content.

All code is placed in the same source file. After debugging, the copy is submitted to the source code.
Do not use package sentence. Do not use jdk1.7 And above.
The name of the main class must be: Main，Otherwise, it will be treated as invalid code.
When submitting programs, pay attention to selecting the desired language type and compiler type.

Solution I

[ideas]

When N=2, it is assumed that the two numbers are a and b
1. The combination of any two numbers must be a multiple of their common divisor. Assuming d = gcd(a,b), the number rounded up by a and B must be a multiple of D.
2. If d = GCD (a, b) > 1, it can be obtained from Article 1 that all the numbers of non-D multiples cannot be rounded up. That is, there are infinite numbers that cannot be summed up.
3. If d = 1, i.e. a and b are coprime, then according to peishu theorem, the upper limit of the largest number that cannot be aggregated is (a- 1)*(b - 1) - 1.
stay Number not available In the question, what we study is the maximum number that can not be rounded up when there are two numbers, while this question is multiple numbers.
Reasoning to N numbers, although it can not accurately represent the maximum number that can not be rounded up. However, increasing the number makes it more possible to choose the number, which is helpful to make up the number, so it plays a role in narrowing the upper limit. For this question, if the numbers within 100 * 99 − 100 − 99 = 9701 can be rounded up, then all numbers can be rounded up.

Then this problem is transformed into a complete knapsack problem: there are N items, each item is infinite, each item can choose any one, can 9701 get all together.

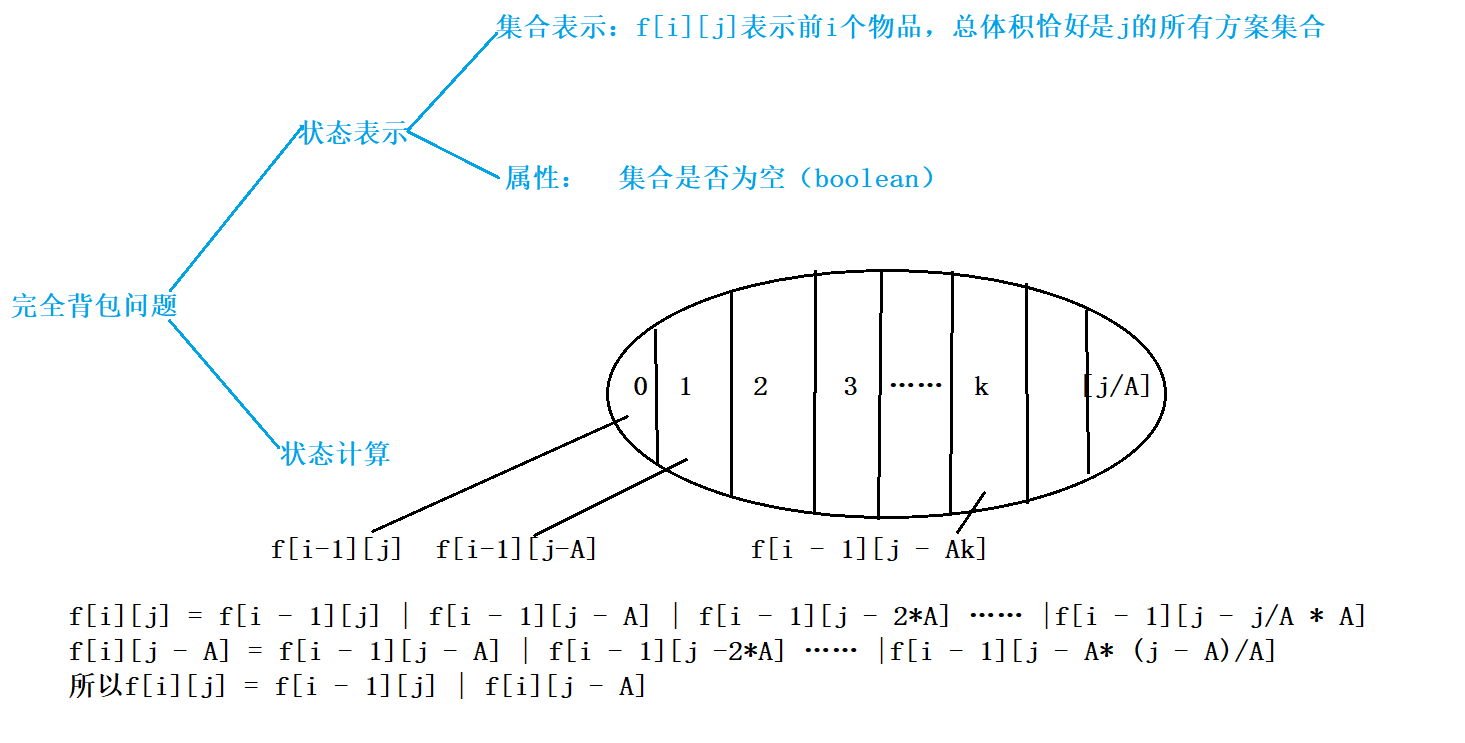
import java.util.Scanner;

class Main{
    static int N = 10010;
    static int a[] = new int[110];
    static boolean f[][] = new boolean [110][N];
    //Euclidean algorithm: gcd(a,b)=gcd(b,a%b). When the remainder is 0, the divisor of the current formula is gcd of a and B.
    public static int gcd(int a, int b){
        if( b == 0) return a;
        return gcd( b, a % b );
    }
    public static void main(String args[]){

        Scanner reader = new Scanner(System.in);
        int n = reader.nextInt();
        for(int i = 1; i <= n; i ++) a[i] = reader.nextInt();
        int d = 0; // Common divisor
        
        for(int i = 1; i <= n; i ++)
            d = gcd(a[i], d);  //gcd(2,0) = 2
        if( d != 1) System.out.println("INF");
        else{
            f[0][0] = true;
            for(int i = 1; i <= n; i ++)
                for(int j = 0; j < N; j ++){
                    f[i][j] |= f[i - 1][j];
                    if( j >= a[i]) f[i][j] |= f[i][j - a[i]];
                }
            int res = 0;
            for(int i = 1; i < N; i ++)
                if( ! f[n][i] ) res ++;
            System.out.println(res);
            
            
        }
    }
}

Solution II

[ideas]
This is a math problem
The essence is the judgment equation ax+ a1x1 +... + anxn=c (a is the number of steamed buns per cage)
Whether there is a solution or not is the number of INF solutions output
According to Euclid's theorem:
ax+by=c
1. If a and b are coprime, then x and y must have solutions and there are infinite solutions
If we want to make the solution x, Y > = 0, then make ax+by=c have no solution (that is, there is a range of c that can not be rounded up), ab-a-b

2. If a and B are not coprime, the existence of a solution cannot be guaranteed, that is, there are an infinite number of C that cannot be summed up (the necessary and sufficient condition for the existence of a solution is: c%gcd(a,b)==0)

package Eighth session;

import java.util.Scanner;

/**
* @author JohnnyLin
* @version Creation Time: 2020 May 24, 2014 10:10:39 PM
*/
public class t08_Make up the number of steamed stuffed buns {
	static int n,g;
	static int a[]=new int[101];
	static boolean[] dp=new boolean[10000];
	public static void main(String[] args) {
		Scanner reader=new Scanner(System.in);
		n=reader.nextInt();
		//Note that 0 can be rounded up
		dp[0]=true;
		for (int i = 1; i <= n; i++) {
			a[i]=reader.nextInt();
			
			if(i==1) g=a[i];//Initialize maximum common divisor
			else g=gcd(a[i],g);
			//Add a[i] this cage. a[i] these numbers can be gathered from the original number
			for(int j=0;j<10000-a[i];j++) {
				if(dp[j]) dp[j+a[i]]=true;
			}
		}
		if(g!=1) {
			System.out.println("INF");
			System.exit(0);
		}
		int ans=0;
		for(int j=0;j<10000;j++) {
			if(!dp[j]) {
				ans++;
			}
		}
		System.out.println(ans);

	}
	/**
	 * @param a
	 * @param b
	 * @return
	 * gcd(4,6)==2
	 * gcd(3,4)==1
	 */
	private static int gcd(int a, int b) {
		//division algorithm 
		if(b==0)return a;
		return gcd(b,a%b);
	}

}