Title Description
Given a tree with a size of ∼ nn ∼ it has ∼ nn nodes and ∼ n - 1n − 1 edges. The nodes are numbered from ∼ 1 \sim n1 ∼ n. Initially, each node has a number of ∼ 1 \sim n1 ∼ n, and each number of ∼ 1 \sim n1 ∼ n only appears on exactly one node.
Next, you need to delete the edge exactly − n - 1n − 1 times. Each time, you need to select an edge that has not been deleted. At this time, the numbers on the two nodes connected by this edge will be exchanged, and then this edge will be deleted.
After n - 1n − 1 operation, all edges will be deleted. At this time, the node numbers where the number ∼ 1 \sim n1 ∼ n ∼ is located are arranged in order from small to large to obtain an arrangement ∼ P of node numbers_ iPi. Now, please find out the minimum dictionary order P under the optimal operation scheme_ iPi.
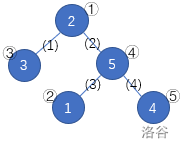
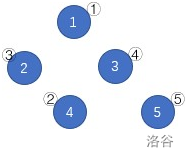
As shown in the figure above, the numbers ∼ 1 \sim 51 ∼ 5 in the blue circle are at nodes ②, ①, ③, ⑤ and ④ respectively. Delete all edges in the order of (1) (4) (3) (2), and the tree becomes the following figure. The node numbers obtained in numerical order are arranged as ① ③ ④ ② ⑤, which is the smallest dictionary order among all possible results.
Input format
The input of this question contains multiple groups of test data.
The first line is a positive integer, {TT, indicating the number of data groups.
For each set of test data:
The first line is an integer {nn, which represents the size of the tree.
In the second line, there are ^ nn integers. The ^ i (1 \leq i \leq n)i(1 ≤ i ≤ n) integer represents the node number where the number ^ ii ^ is initially located.
Next, in line n - 1n − 1, there are two integers xx, yy in each line, representing an edge connecting node xx and node yy.
Output format
For each group of test data, a total of ^ nn integers separated by spaces are output in a line, representing ^ P with the smallest dictionary order under the optimal operation scheme_ iPi.
Input and output samples
Enter #1 copy
4 5 2 1 3 5 4 1 3 1 4 2 4 4 5 5 3 4 2 1 5 1 2 2 3 3 4 4 5 5 1 2 5 3 4 1 2 1 3 1 4 1 5 10 1 2 3 4 5 7 8 9 10 6 1 2 1 3 1 4 1 5 5 6 6 7 7 8 8 9 9 10
Output #1 copy
1 3 4 2 5 1 3 5 2 4 2 3 1 4 5 2 3 4 5 6 1 7 8 9 10
Description / tips
[data range]
| Test point number | n \leqn≤ | Special properties |
|---|---|---|
| 1 \sim 21∼2 | 10 | nothing |
| 3 \sim 43∼4 | 160 | The form of a tree is a chain |
| 5 \sim 75∼7 | 2000 | ditto |
| 8 \sim 98∼9 | 160 | There are nodes with degrees of − n - 1n − 1 |
| 10 \sim 1210∼12 | 2000 | ditto |
| 13 \sim 1613∼16 | 160 | nothing |
| 17 \sim 2017∼20 | 2000 | nothing |
For all test points: 1 \leq T \leq 101 ≤ T ≤ 10, it is guaranteed that a tree is given.
Upper Code:
#include<cstdio>
#include<vector>
using namespace std;
#define rep(i,__l,__r) for(int i=__l,i##_end_=__r;i<=i##_end_;++i)
#define fep(i,__l,__r) for(int i=__l,i##_end_=__r;i>=i##_end_;--i)
#define writc(a,b) fwrit(a),putchar(b)
#define mp(a,b) make_pair(a,b)
#define ft first
#define sd second
#define LL long long
#define ull unsigned long long
#define pii pair<int,int>
// #define FILEOI
#define cg (c=getchar())
template<class T>inline void qread(T& x){
char c;bool f=0;
while(cg<'0'||'9'<c)if(c=='-')f=1;
for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
if(f)x=-x;
}
inline int qread(){
int x=0;char c;bool f=0;
while(cg<'0'||'9'<c)if(c=='-')f=-1;
for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
return f?-x:x;
}
#undef cg
template<class T,class... Args>inline void qread(T& x,Args&... args){qread(x),qread(args...);}
template<class T>inline T Max(const T x,const T y){return x>y?x:y;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
inline void getInv(int inv[],const int lim,const int MOD){
inv[0]=inv[1]=1;for(int i=2;i<=lim;++i)inv[i]=1ll*inv[MOD%i]*(MOD-MOD/i)%MOD;
}
template<class T>void fwrit(const T x){
if(x<0)return (void)(putchar('-'),fwrit(-x));
if(x>9)fwrit(x/10);putchar(x%10^48);
}
const int MAXN=2000;
struct edge{
int to,nxt;
edge(){}
edge(const int T,const int N):to(T),nxt(N){}
}e[(MAXN<<1)+5];
int tail[MAXN+5],ecnt,siz[MAXN+5];
inline void add_edge(const int u,const int v){
++siz[u],++siz[v];
e[++ecnt]=edge(v,tail[u]);tail[u]=ecnt;
e[++ecnt]=edge(u,tail[v]);tail[v]=ecnt;
}
int N,minp;
int pt[MAXN+5];
int pre[MAXN+5][MAXN+5],nxt[MAXN+5][MAXN+5];
//This side is the precursor and successor
int rt[MAXN+5][MAXN+5][2];
//Front root node and rear root node of an edge of point u
int len[MAXN+5][MAXN+5];
//The length of the chain in which this edge is located
inline void init(){
qread(N);
ecnt=0;
rep(i,1,N)qread(pt[i]),tail[i]=siz[i]=0;
rep(i,1,N+1)rep(j,1,N+1)len[i][j]=pre[i][j]=nxt[i][j]=rt[i][j][0]=rt[i][j][1]=0;
int u,v;
rep(i,1,N-1){
qread(u,v);
add_edge(u,v);
pre[u][v]=pre[v][u]=nxt[u][v]=nxt[v][u]=0;
rt[u][v][0]=rt[u][v][1]=v;
rt[v][u][0]=rt[v][u][1]=u;
len[u][v]=len[v][u]=1;
}
}
void findPath(const int u,const int p){//Current node, previous node
int a=rt[u][p][0],b=rt[u][p][1],ta,tb;
//a: The front root of the side that comes; b: The back root of the edge
if(p==N+1){//This is the starting point
for(int i=tail[u],v;i;i=e[i].nxt){//Which way does it take off
v=e[i].to;
ta=rt[u][v][0],tb=rt[u][v][1];
if(ta!=v || (pre[u][p]==tb && len[u][ta]<siz[u]))
//Condition 1: if this edge already has a starting point and is not itself
//Condition 2: if the following edge has been connected to the tail end, and the length of this chain cannot meet the requirement to connect all edges
continue;//Then you can't connect edge {u,p} with edge {u,v}
findPath(v,u);//Otherwise, it is feasible
}
}
else{
if(p==b){//If the edge {u,p} is not specified after which edge must be deleted, you can consider enumerating an edge to follow
if(pre[u][N+1]==0 && (nxt[u][N+1]!=a || len[u][a]==siz[u]))//You can consider landing at point u and meet the following conditions:
//If the last deleted edge of this point has not been specified (must be met)
//And:
//1. If this link begins, then if it must be satisfied that all edges are on this chain
//2. If the beginning is not connected, the length is optional
minp=Min(minp,u);//If satisfied, u can be used as a landing point
for(int i=tail[u],v;i;i=e[i].nxt){//Assuming u is a transit point, another edge is enumerated as the outgoing edge of edge {u,p} and connected to its tail
v=e[i].to;
ta=rt[u][v][0],tb=rt[u][v][1];
if(a==ta || ta!=v || nxt[u][N+1]==v)//The first big case
//If the two sides are already on the same chain
//Or this edge is not a starting edge, that is, there is something in front of the enumeration edge
//Or the enumeration edge is a takeoff edge, that is to ensure that it is the edge that must be deleted first for all edges of u
continue;//Then the current edge {u,p} cannot be connected to this enumeration edge
if(nxt[u][N+1]==a && pre[u][N+1]==tb && len[u][a]+len[u][ta]<siz[u])
//If these two edges belong to the tail and head of the linked list deleted first and last at this point
//Then their combination must be equal to the sum of the number of all edges
//Otherwise, this is the case of early autism
continue;
findPath(v,u);//If none of the above is satisfied, then this side is legal
}
}
else findPath(nxt[u][p],u);//Otherwise, we can only access this side according to the previous regulations
}
}
inline void merge(const int u,const int a,const int b){
//Function condition: take the linked list where a is located as the front linked list
//And a is the tail of the front chain list and b is the header of the rear chain
int ta=rt[u][a][0],tb=rt[u][b][1];
nxt[u][a]=b;
pre[u][b]=a;
for(int i=ta;i && i!=N+1;i=nxt[u][i]){
//Basic operations for accessing linked lists
//Update the front root and rear root of each point
rt[u][i][0]=ta;
rt[u][i][1]=tb;
}
len[u][ta]+=len[u][b];
}
bool getMark(const int u,const int p){//Restore the path and mark it
//If the path finds the end point, it returns 1, otherwise it returns 0
if(u==minp){//If you find the end
pre[u][N+1]=p;//Set this edge as the last deleted edge
nxt[u][p]=N+1;//And mark the next edge of this edge as N+1, indicating that this edge is deleted last
return 1;
}
int a=rt[u][p][0],b=rt[u][p][1],ta,tb;
if(p==N+1){//This is the departure point
for(int i=tail[u],v;i;i=e[i].nxt){
v=e[i].to;
ta=rt[u][v][0],tb=rt[u][v][1];
if(ta!=v || (pre[u][N+1]==tb && len[u][ta]<siz[u]))
//If there is something in front of the enumeration edge, it must not be followed by the starting edge, because there is something in front of it
//Or the enumeration edge is connected to the end, but the single chain is not long enough to include all edges in the chain
continue;//Then this edge is definitely not on the path, you can skip it directly
if(getMark(v,u)){//If this is the right path
nxt[u][N+1]=v;//Because point u is the takeoff point, record this edge as the takeoff edge of U
pre[u][v]=N+1;//At the same time, mark the precursor of this side and echo with the front if (this is not Chinese...)
return 1;
}
}
}
else{//If point u is a transit point, consider enumerating transit edges
if(p==b){//If there are no other edges behind this edge on the chain
for(int i=tail[u],v;i;i=e[i].nxt){
v=e[i].to;
ta=rt[u][v][0],tb=rt[u][v][1];
if(a==ta || ta!=v || nxt[u][N+1]==v)//Refer to the comment at the same location in findPath()
continue;
if(nxt[u][N+1]==a && pre[u][N+1]==tb && len[u][a]+len[u][ta]<siz[u])//Also refer to the same location in findPath()
continue;
if(getMark(v,u)){
merge(u,p,v);//Merge the linked list into one
return 1;
}
}
}
else getMark(nxt[u][p],u);
}
return 0;
}
signed main(){
#ifdef FILEOI
freopen("rdata.out","r",stdin);
freopen("file.out","w",stdout);
#endif
int T=qread();
while(T--){
init();
if(N==1){
writc(1,'\n');
continue;
}
rep(i,1,N){
minp=N+1;
findPath(pt[i],N+1);
// printf("%d\n",minp);
getMark(pt[i],N+1);
writc(minp,' ');
}
putchar('\n');
}
return 0;
}