1. Principle of xgboost ranking feature importance

xgboost calculates which feature to choose as the segmentation point according to the gain of the structure fraction, and the importance of a feature is the sum of the number of times it appears in all trees. That is to say, the more attribute is used to construct decision tree in the model, the more important it is.
Method for sorting the importance of 2 xgboost features

1. xgboost can get feature importance through get_score
   for importance_type in ('weight', 'gain', 'cover', 'total_gain', 'total_cover'):
   print('%s: ' % importance_type, bst.get_score(importance_type=importance_type))
   weight - The number of times the feature is used to segment samples in all trees.
   Gain - Average gain in all trees.
   cover - Average coverage when using this feature in a tree. (Not particularly clear yet)

2. Use plot_importance to draw the importance ranking of each feature

3. We can select features from the importance of features by testing multiple thresholds and using indicators to measure the classifier's quality.
   Here is an empirical analysis using kaggle's heartdisease data

#Use get_score in xgb.train to get weight, gain, and cover
params={        'max_depth':7,
                'n_estimators':80,
                'learning_rate':0.1, 
                'nthread':4,
                'subsample':1.0,
                'colsample_bytree':0.5,
                'min_child_weight' : 3,
                'seed':1301}
bst = xgb.train(params, xgtrain, num_boost_round=1)
for importance_type in ('weight', 'gain', 'cover', 'total_gain', 'total_cover'):
    print('%s: ' % importance_type, bst.get_score(importance_type=importance_type))
import graphviz
xgb.plot_tree(bst)
plt.show()

The results are as follows:
weight: {'slope': 2, 'sex': 2, 'age': 7, 'chol': 13, 'trestbps': 9, 'restecg': 2}
gain: {'slope': 4.296458304, 'sex': 2.208011625, 'age': 0.8395543860142858, 'chol': 0.6131722695384615, 'trestbps': 0.49512829022222227, 'restecg': 0.679761901}
cover: {'slope': 116.5, 'sex': 106.0, 'age': 24.714285714285715, 'chol': 22.846153846153847, 'trestbps': 18.555555555555557, 'restecg': 18.0}
total_gain: {'slope': 8.592916608, 'sex': 4.41602325, 'age': 5.8768807021, 'chol': 7.971239503999999, 'trestbps': 4.456154612000001, 'restecg': 1.359523802}
total_cover: {'slope': 233.0, 'sex': 212.0, 'age': 173.0, 'chol': 297.0, 'trestbps': 167.0, 'restecg': 36.0}

from sklearn.feature_selection import SelectFromModel
model = xgb.XGBClassifier()
model.fit(X_train, y_train)
#Plot_importance; use plot_importance to draw the importance order of each feature
from xgboost import plot_importance
plot_importance(model)
plt.show()

The results are as follows: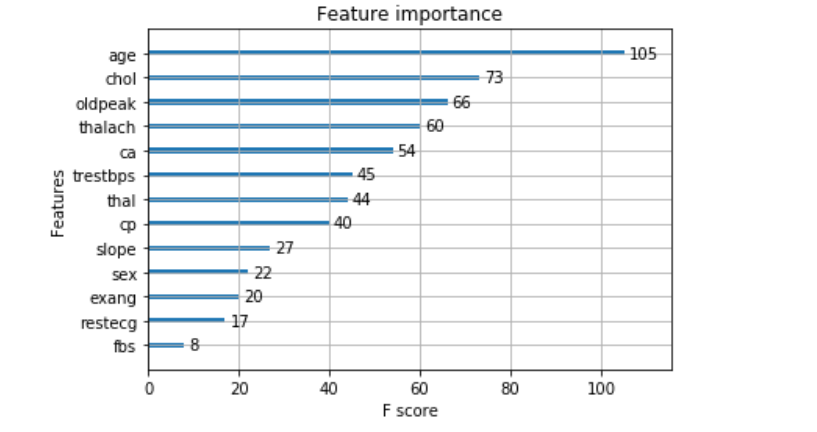

#We can select features from the importance of features by testing multiple thresholds. Specifically, the characteristic importance of each input variable essentially allows us to#Test each feature subset by importance.
# make predictions for test data and evaluate
y_pred = model.predict(X_test)
predictions = [round(value) for value in y_pred]
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
# Fit model using each importance as a threshold
thresholds = np.sort(model.feature_importances_)
for thresh in thresholds:
	# select features using threshold
	selection = SelectFromModel(model, threshold=thresh, prefit=True)
	select_X_train = selection.transform(X_train)
	# train model
	selection_model = xgb.XGBClassifier()
	selection_model.fit(select_X_train, y_train)
	# eval model
	select_X_test = selection.transform(X_test)
	y_pred = selection_model.predict(select_X_test)
	predictions = [round(value) for value in y_pred]
	accuracy = accuracy_score(y_test, predictions)
	print("Thresh=%.3f, n=%d, Accuracy: %.2f%%" % (thresh, select_X_train.shape[1], accuracy*100.0))

Accuracy: 84.62%
Thresh=0.025, n=13, Accuracy: 84.62%
Thresh=0.026, n=12, Accuracy: 80.22%
Thresh=0.026, n=11, Accuracy: 79.12%
Thresh=0.028, n=10, Accuracy: 76.92%
Thresh=0.032, n=9, Accuracy: 78.02%
Thresh=0.036, n=8, Accuracy: 80.22%
Thresh=0.041, n=7, Accuracy: 76.92%
Thresh=0.066, n=6, Accuracy: 76.92%
Thresh=0.085, n=5, Accuracy: 84.62%
Thresh=0.146, n=4, Accuracy: 80.22%
Thresh=0.151, n=3, Accuracy: 76.92%
Thresh=0.163, n=2, Accuracy: 74.73%
Thresh=0.174, n=1, Accuracy: 78.02%
From the above results, it can be seen that with the increase of threshold, the number of features decreases, and the accuracy decreases. In general, cross validation may be a more useful strategy for model evaluation. This will be implemented in the next xgb.cv article.