The second bullet of BUUCTF-RSA check-in question, interesting or difficult RSA questions are placed separately in the column BUUCTF RSA column_ Xiaohan's blog - CSDN blog
Dangerous RSA (low encryption index attack)
subject
n=0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793L
e=0x3
c=0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
so,how to get the message?
Problem solving ideas
The title only gives n, e, c, and the modulus n is very large, which is difficult to decompose
However, we notice that the public key e = 3, which brings great insecurity to encryption
This can be used to attack small encryption indexes:
- If me < n, then m can be obtained by c directly to the third power
- If me > N, let me = c + kn, then m can be obtained by (c+kn) to the third power, where k is traversed
Attach Code:
import gmpy2
import binascii
n=0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793
e=0x3
c=0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
k = 0
while(True):
#gmpy2.iroot(x,n) x open to the nth power root
#The return value m is the calculation result of square root, and f is the bool variable, indicating whether x can be square root
m, f = gmpy2.iroot(c+k*n, e)
if f:
m = hex(m)[2:]
print("Plaintext data is: 0 x" + m)
flag = binascii.unhexlify(m)
print(flag) #flag{25df8caf006ee5db94d48144c33b2c3b}
break
k += 1
In this problem, the result is obtained by directly prescribing the square
flag
flag{25df8caf006ee5db94d48144c33b2c3b}
[hdctf2019] basic RSA (basic questions)
subject
We are given a code file attachment Py, as follows
import gmpy2 from Crypto.Util.number import * from binascii import a2b_hex,b2a_hex flag = "*****************" p = 262248800182277040650192055439906580479 q = 262854994239322828547925595487519915551 e = 65533 n = p*q c = pow(int(b2a_hex(flag),16),e,n) print c # 27565231154623519221597938803435789010285480123476977081867877272451638645710
Problem solving ideas
Run it first
There is a bit of a hole here. Because I use Python 3, I need to modify some places to solve the error reporting problem. The modifications are as follows:
c = pow(int(b2a_hex(bytes(flag, encoding = "utf8")),16),e,n) print(c)
- b2a_ The parameter accepted by hex () must be of type bytes, and cast is performed here
- The print function should be bracketed in Python 3
Analyze the code:
b2a_hex() converts byte type data to hexadecimal data, and then converts it to decimal with int()
Finally, the pow() function is used for modular power operation, C = flag (E)% N, that is, the flag is encrypted with RSA
The encryption output results are as follows:
9544552122426002996962843810441848397036784063191487784065817764908998519819
Well, I don't know what this wave of operations is doing. Maybe I'm teaching you how to use RSA to encrypt text? (squint smile. jpg)
So where is the real flag
Notice that there is a string of data in the comments on the last line of the code, and try to decrypt it
Attach Code:
import gmpy2
import binascii
p = 262248800182277040650192055439906580479
q = 262854994239322828547925595487519915551
e = 65533
n = p*q
c = 27565231154623519221597938803435789010285480123476977081867877272451638645710
d = gmpy2.invert(e,(p-1)*(q-1)) # Inverse element, de = 1 mod fai(n)
m = gmpy2.powmod(c,d,n)# Power modulus
flag = binascii.unhexlify(hex(m)[2:])
print(flag) #flag{B4by_Rs4}
get flag! This line of comment is the ciphertext text
flag
flag{B4by_Rs4}
Babyrsa (basic questions)
subject
p+q : 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
(p+1)(q+1) : 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
e : 0xe6b1bee47bd63f615c7d0a43c529d219
d : 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
enc_flag : 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a
Problem solving ideas
This problem directly gives the private key d, but does not give the modulus n, so we need to find n = pq from p+q and (p+1)(q+1)
It's very simple to get:
(p+1)(q+1) = pq + p + q + 1
pq = (p+1)(q+1) - (p+q) - 1
After getting n, you can get the flag by normal decryption
Attach Code:
import gmpy2
import binascii
#p+q = 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
#(p+1)(q+1) = 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
e = 0xe6b1bee47bd63f615c7d0a43c529d219
d = 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
enc_flag = 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a
a = 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
b = 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
n = b - a - 1 #Calculation modulus n
m = gmpy2.powmod(enc_flag, d, n) #decrypt
print("The plaintext data is:" + hex(m))
flag = binascii.unhexlify(hex(m)[2:])
print(flag)
flag
flag{cc7490e-78ab-11e9-b422-8ba97e5da1fd}
Rsa5 (multi N decomposition)
subject
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-c6x6udkc-1626313465179) (C: \ users \ xiao_han \ appdata \ roaming \ typora \ typora user images \ image-202107092753224. PNG)]
The encryption index e and the encryption result c corresponding to different modulus n are given. A total of 20 groups of nc are given
Problem solving ideas
Since e in this problem is not a small index, it can not be solved by the Chinese remainder theorem like RSA4
Because we have a total of 20 modules n, try whether there will be two large prime factors of n that are the same
Because p and q are prime numbers, the factor of n is only {1, p, q, n}
Directly calculate the common divisor of two n. if it is greater than 1, it must be one of p or q
With one of p or Q, n = p * q can be decomposed to calculate the private key d for decryption
Attach Code:
import gmpy2
import binascii
def solve(nList, cList):
for i in range(len(nList)):
for j in range(i+1, len(nList)):
p = gmpy2.gcd(nList[i], nList[j]) #Calculate the maximum common divisor
if p != 1: #If there is a maximum common divisor, it is a large prime factor shared by n[i] and n[j], that is, p or q
print("n[%d]and n[%d]The common divisor is\n%d" % (i,j,p))
q = nList[i] // p
print("decompose n[%d]obtain:\n%d =\n%d * \n%d" % (i,nList[i],p,q))
d = gmpy2.invert(e,(p-1)*(q-1)) #Calculate the inverse of e, that is, the private key d
m = gmpy2.powmod(cList[i], d, nList[i]) #Modular exponentiation, decryption
return (binascii.unhexlify(hex(m)[2:]))
if __name__ == "__main__":
e = 65537
#========== n c ==========
n1 = 20474918894051778533305262345601880928088284471121823754049725354072477155873778848055073843345820697886641086842612486541250183965966001591342031562953561793332341641334302847996108417466360688139866505179689516589305636902137210185624650854906780037204412206309949199080005576922775773722438863762117750429327585792093447423980002401200613302943834212820909269713876683465817369158585822294675056978970612202885426436071950214538262921077409076160417436699836138801162621314845608796870206834704116707763169847387223307828908570944984416973019427529790029089766264949078038669523465243837675263858062854739083634207
c1 = 974463908243330865728978769213595400782053398596897741316275722596415018912929508637393850919224969271766388710025195039896961956062895570062146947736340342927974992616678893372744261954172873490878805483241196345881721164078651156067119957816422768524442025688079462656755605982104174001635345874022133045402344010045961111720151990412034477755851802769069309069018738541854130183692204758761427121279982002993939745343695671900015296790637464880337375511536424796890996526681200633086841036320395847725935744757993013352804650575068136129295591306569213300156333650910795946800820067494143364885842896291126137320
n2 = 20918819960648891349438263046954902210959146407860980742165930253781318759285692492511475263234242002509419079545644051755251311392635763412553499744506421566074721268822337321637265942226790343839856182100575539845358877493718334237585821263388181126545189723429262149630651289446553402190531135520836104217160268349688525168375213462570213612845898989694324269410202496871688649978370284661017399056903931840656757330859626183773396574056413017367606446540199973155630466239453637232936904063706551160650295031273385619470740593510267285957905801566362502262757750629162937373721291789527659531499435235261620309759
c2 = 15819636201971185538694880505120469332582151856714070824521803121848292387556864177196229718923770810072104155432038682511434979353089791861087415144087855679134383396897817458726543883093567600325204596156649305930352575274039425470836355002691145864435755333821133969266951545158052745938252574301327696822347115053614052423028835532509220641378760800693351542633860702225772638930501021571415907348128269681224178300248272689705308911282208685459668200507057183420662959113956077584781737983254788703048275698921427029884282557468334399677849962342196140864403989162117738206246183665814938783122909930082802031855
n3 = 25033254625906757272369609119214202033162128625171246436639570615263949157363273213121556825878737923265290579551873824374870957467163989542063489416636713654642486717219231225074115269684119428086352535471683359486248203644461465935500517901513233739152882943010177276545128308412934555830087776128355125932914846459470221102007666912211992310538890654396487111705385730502843589727289829692152177134753098649781412247065660637826282055169991824099110916576856188876975621376606634258927784025787142263367152947108720757222446686415627479703666031871635656314282727051189190889008763055811680040315277078928068816491
c3 = 4185308529416874005831230781014092407198451385955677399668501833902623478395669279404883990725184332709152443372583701076198786635291739356770857286702107156730020004358955622511061410661058982622055199736820808203841446796305284394651714430918690389486920560834672316158146453183789412140939029029324756035358081754426645160033262924330248675216108270980157049705488620263485129480952814764002865280019185127662449318324279383277766416258142275143923532168798413011028271543085249029048997452212503111742302302065401051458066585395360468447460658672952851643547193822775218387853623453638025492389122204507555908862
n4 = 21206968097314131007183427944486801953583151151443627943113736996776787181111063957960698092696800555044199156765677935373149598221184792286812213294617749834607696302116136745662816658117055427803315230042700695125718401646810484873064775005221089174056824724922160855810527236751389605017579545235876864998419873065217294820244730785120525126565815560229001887622837549118168081685183371092395128598125004730268910276024806808565802081366898904032509920453785997056150497645234925528883879419642189109649009132381586673390027614766605038951015853086721168018787523459264932165046816881682774229243688581614306480751
c4 = 4521038011044758441891128468467233088493885750850588985708519911154778090597136126150289041893454126674468141393472662337350361712212694867311622970440707727941113263832357173141775855227973742571088974593476302084111770625764222838366277559560887042948859892138551472680654517814916609279748365580610712259856677740518477086531592233107175470068291903607505799432931989663707477017904611426213770238397005743730386080031955694158466558475599751940245039167629126576784024482348452868313417471542956778285567779435940267140679906686531862467627238401003459101637191297209422470388121802536569761414457618258343550613
n5 = 22822039733049388110936778173014765663663303811791283234361230649775805923902173438553927805407463106104699773994158375704033093471761387799852168337898526980521753614307899669015931387819927421875316304591521901592823814417756447695701045846773508629371397013053684553042185725059996791532391626429712416994990889693732805181947970071429309599614973772736556299404246424791660679253884940021728846906344198854779191951739719342908761330661910477119933428550774242910420952496929605686154799487839923424336353747442153571678064520763149793294360787821751703543288696726923909670396821551053048035619499706391118145067
c5 = 15406498580761780108625891878008526815145372096234083936681442225155097299264808624358826686906535594853622687379268969468433072388149786607395396424104318820879443743112358706546753935215756078345959375299650718555759698887852318017597503074317356745122514481807843745626429797861463012940172797612589031686718185390345389295851075279278516147076602270178540690147808314172798987497259330037810328523464851895621851859027823681655934104713689539848047163088666896473665500158179046196538210778897730209572708430067658411755959866033531700460551556380993982706171848970460224304996455600503982223448904878212849412357
n6 = 21574139855341432908474064784318462018475296809327285532337706940126942575349507668289214078026102682252713757703081553093108823214063791518482289846780197329821139507974763780260290309600884920811959842925540583967085670848765317877441480914852329276375776405689784571404635852204097622600656222714808541872252335877037561388406257181715278766652824786376262249274960467193961956690974853679795249158751078422296580367506219719738762159965958877806187461070689071290948181949561254144310776943334859775121650186245846031720507944987838489723127897223416802436021278671237227993686791944711422345000479751187704426369
c6 = 20366856150710305124583065375297661819795242238376485264951185336996083744604593418983336285185491197426018595031444652123288461491879021096028203694136683203441692987069563513026001861435722117985559909692670907347563594578265880806540396777223906955491026286843168637367593400342814725694366078337030937104035993569672959361347287894143027186846856772983058328919716702982222142848848117768499996617588305301483085428547267337070998767412540225911508196842253134355901263861121500650240296746702967594224401650220168780537141654489215019142122284308116284129004257364769474080721001708734051264841350424152506027932
n7 = 25360227412666612490102161131174584819240931803196448481224305250583841439581008528535930814167338381983764991296575637231916547647970573758269411168219302370541684789125112505021148506809643081950237623703181025696585998044695691322012183660424636496897073045557400768745943787342548267386564625462143150176113656264450210023925571945961405709276631990731602198104287528528055650050486159837612279600415259486306154947514005408907590083747758953115486124865486720633820559135063440942528031402951958557630833503775112010715604278114325528993771081233535247118481765852273252404963430792898948219539473312462979849137
c7 = 19892772524651452341027595619482734356243435671592398172680379981502759695784087900669089919987705675899945658648623800090272599154590123082189645021800958076861518397325439521139995652026377132368232502108620033400051346127757698623886142621793423225749240286511666556091787851683978017506983310073524398287279737680091787333547538239920607761080988243639547570818363788673249582783015475682109984715293163137324439862838574460108793714172603672477766831356411304446881998674779501188163600664488032943639694828698984739492200699684462748922883550002652913518229322945040819064133350314536378694523704793396169065179
n8 = 22726855244632356029159691753451822163331519237547639938779517751496498713174588935566576167329576494790219360727877166074136496129927296296996970048082870488804456564986667129388136556137013346228118981936899510687589585286517151323048293150257036847475424044378109168179412287889340596394755257704938006162677656581509375471102546261355748251869048003600520034656264521931808651038524134185732929570384705918563982065684145766427962502261522481994191989820110575981906998431553107525542001187655703534683231777988419268338249547641335718393312295800044734534761692799403469497954062897856299031257454735945867491191
c8 = 6040119795175856407541082360023532204614723858688636724822712717572759793960246341800308149739809871234313049629732934797569781053000686185666374833978403290525072598774001731350244744590772795701065129561898116576499984185920661271123665356132719193665474235596884239108030605882777868856122378222681140570519180321286976947154042272622411303981011302586225630859892731724640574658125478287115198406253847367979883768000812605395482952698689604477719478947595442185921480652637868335673233200662100621025061500895729605305665864693122952557361871523165300206070325660353095592778037767395360329231331322823610060006
n9 = 23297333791443053297363000786835336095252290818461950054542658327484507406594632785712767459958917943095522594228205423428207345128899745800927319147257669773812669542782839237744305180098276578841929496345963997512244219376701787616046235397139381894837435562662591060768476997333538748065294033141610502252325292801816812268934171361934399951548627267791401089703937389012586581080223313060159456238857080740699528666411303029934807011214953984169785844714159627792016926490955282697877141614638806397689306795328344778478692084754216753425842557818899467945102646776342655167655384224860504086083147841252232760941
c9 = 5418120301208378713115889465579964257871814114515046096090960159737859076829258516920361577853903925954198406843757303687557848302302200229295916902430205737843601806700738234756698575708612424928480440868739120075888681672062206529156566421276611107802917418993625029690627196813830326369874249777619239603300605876865967515719079797115910578653562787899019310139945904958024882417833736304894765433489476234575356755275147256577387022873348906900149634940747104513850154118106991137072643308620284663108283052245750945228995387803432128842152251549292698947407663643895853432650029352092018372834457054271102816934
n10 = 28873667904715682722987234293493200306976947898711255064125115933666968678742598858722431426218914462903521596341771131695619382266194233561677824357379805303885993804266436810606263022097900266975250431575654686915049693091467864820512767070713267708993899899011156106766178906700336111712803362113039613548672937053397875663144794018087017731949087794894903737682383916173267421403408140967713071026001874733487295007501068871044649170615709891451856792232315526696220161842742664778581287321318748202431466508948902745314372299799561625186955234673012098210919745879882268512656931714326782335211089576897310591491
c10 = 9919880463786836684987957979091527477471444996392375244075527841865509160181666543016317634963512437510324198702416322841377489417029572388474450075801462996825244657530286107428186354172836716502817609070590929769261932324275353289939302536440310628698349244872064005700644520223727670950787924296004296883032978941200883362653993351638545860207179022472492671256630427228461852668118035317021428675954874947015197745916918197725121122236369382741533983023462255913924692806249387449016629865823316402366017657844166919846683497851842388058283856219900535567427103603869955066193425501385255322097901531402103883869
n11 = 22324685947539653722499932469409607533065419157347813961958075689047690465266404384199483683908594787312445528159635527833904475801890381455653807265501217328757871352731293000303438205315816792663917579066674842307743845261771032363928568844669895768092515658328756229245837025261744260614860746997931503548788509983868038349720225305730985576293675269073709022350700836510054067641753713212999954307022524495885583361707378513742162566339010134354907863733205921845038918224463903789841881400814074587261720283879760122070901466517118265422863420376921536734845502100251460872499122236686832189549698020737176683019
c11 = 1491527050203294989882829248560395184804977277747126143103957219164624187528441047837351263580440686474767380464005540264627910126483129930668344095814547592115061057843470131498075060420395111008619027199037019925701236660166563068245683975787762804359520164701691690916482591026138582705558246869496162759780878437137960823000043988227303003876410503121370163303711603359430764539337597866862508451528158285103251810058741879687875218384160282506172706613359477657215420734816049393339593755489218588796607060261897905233453268671411610631047340459487937479511933450369462213795738933019001471803157607791738538467
n12 = 27646746423759020111007828653264027999257847645666129907789026054594393648800236117046769112762641778865620892443423100189619327585811384883515424918752749559627553637785037359639801125213256163008431942593727931931898199727552768626775618479833029101249692573716030706695702510982283555740851047022672485743432464647772882314215176114732257497240284164016914018689044557218920300262234652840632406067273375269301008409860193180822366735877288205783314326102263756503786736122321348320031950012144905869556204017430593656052867939493633163499580242224763404338807022510136217187779084917996171602737036564991036724299
c12 = 21991524128957260536043771284854920393105808126700128222125856775506885721971193109361315961129190814674647136464887087893990660894961612838205086401018885457667488911898654270235561980111174603323721280911197488286585269356849579263043456316319476495888696219344219866516861187654180509247881251251278919346267129904739277386289240394384575124331135655943513831009934023397457082184699737734388823763306805326430395849935770213817533387235486307008892410920611669932693018165569417445885810825749609388627231235840912644654685819620931663346297596334834498661789016450371769203650109994771872404185770230172934013971
n13 = 20545487405816928731738988374475012686827933709789784391855706835136270270933401203019329136937650878386117187776530639342572123237188053978622697282521473917978282830432161153221216194169879669541998840691383025487220850872075436064308499924958517979727954402965612196081404341651517326364041519250125036424822634354268773895465698920883439222996581226358595873993976604699830613932320720554130011671297944433515047180565484495191003887599891289037982010216357831078328159028953222056918189365840711588671093333013117454034313622855082795813122338562446223041211192277089225078324682108033843023903550172891959673551
c13 = 14227439188191029461250476692790539654619199888487319429114414557975376308688908028140817157205579804059783807641305577385724758530138514972962209062230576107406142402603484375626077345190883094097636019771377866339531511965136650567412363889183159616188449263752475328663245311059988337996047359263288837436305588848044572937759424466586870280512424336807064729894515840552404756879590698797046333336445465120445087587621743906624279621779634772378802959109714400516183718323267273824736540168545946444437586299214110424738159957388350785999348535171553569373088251552712391288365295267665691357719616011613628772175
n14 = 27359727711584277234897157724055852794019216845229798938655814269460046384353568138598567755392559653460949444557879120040796798142218939251844762461270251672399546774067275348291003962551964648742053215424620256999345448398805278592777049668281558312871773979931343097806878701114056030041506690476954254006592555275342579529625231194321357904668512121539514880704046969974898412095675082585315458267591016734924646294357666924293908418345508902112711075232047998775303603175363964055048589769318562104883659754974955561725694779754279606726358588862479198815999276839234952142017210593887371950645418417355912567987
c14 = 3788529784248255027081674540877016372807848222776887920453488878247137930578296797437647922494510483767651150492933356093288965943741570268943861987024276610712717409139946409513963043114463933146088430004237747163422802959250296602570649363016151581364006795894226599584708072582696996740518887606785460775851029814280359385763091078902301957226484620428513604630585131511167015763190591225884202772840456563643159507805711004113901417503751181050823638207803533111429510911616160851391754754434764819568054850823810901159821297849790005646102129354035735350124476838786661542089045509656910348676742844957008857457
n15 = 27545937603751737248785220891735796468973329738076209144079921449967292572349424539010502287564030116831261268197384650511043068738911429169730640135947800885987171539267214611907687570587001933829208655100828045651391618089603288456570334500533178695238407684702251252671579371018651675054368606282524673369983034682330578308769886456335818733827237294570476853673552685361689144261552895758266522393004116017849397346259119221063821663280935820440671825601452417487330105280889520007917979115568067161590058277418371493228631232457972494285014767469893647892888681433965857496916110704944758070268626897045014782837
c15 = 14069112970608895732417039977542732665796601893762401500878786871680645798754783315693511261740059725171342404186571066972546332813667711135661176659424619936101038903439144294886379322591635766682645179888058617577572409307484708171144488708410543462972008179994594087473935638026612679389759756811490524127195628741262871304427908481214992471182859308828778119005750928935764927967212343526503410515793717201360360437981322576798056276657140363332700714732224848346808963992302409037706094588964170239521193589470070839790404597252990818583717869140229811712295005710540476356743378906642267045723633874011649259842
n16 = 25746162075697911560263181791216433062574178572424600336856278176112733054431463253903433128232709054141607100891177804285813783247735063753406524678030561284491481221681954564804141454666928657549670266775659862814924386584148785453647316864935942772919140563506305666207816897601862713092809234429096584753263707828899780979223118181009293655563146526792388913462557306433664296966331469906428665127438829399703002867800269947855869262036714256550075520193125987011945192273531732276641728008406855871598678936585324782438668746810516660152018244253008092470066555687277138937298747951929576231036251316270602513451
c16 = 17344284860275489477491525819922855326792275128719709401292545608122859829827462088390044612234967551682879954301458425842831995513832410355328065562098763660326163262033200347338773439095709944202252494552172589503915965931524326523663289777583152664722241920800537867331030623906674081852296232306336271542832728410803631170229642717524942332390842467035143631504401140727083270732464237443915263865880580308776111219718961746378842924644142127243573824972533819479079381023103585862099063382129757560124074676150622288706094110075567706403442920696472627797607697962873026112240527498308535903232663939028587036724
n17 = 23288486934117120315036919418588136227028485494137930196323715336208849327833965693894670567217971727921243839129969128783853015760155446770590696037582684845937132790047363216362087277861336964760890214059732779383020349204803205725870225429985939570141508220041286857810048164696707018663758416807708910671477407366098883430811861933014973409390179948577712579749352299440310543689035651465399867908428885541237776143404376333442949397063249223702355051571790555151203866821867908531733788784978667478707672984539512431549558672467752712004519300318999208102076732501412589104904734983789895358753664077486894529499
c17 = 10738254418114076548071448844964046468141621740603214384986354189105236977071001429271560636428075970459890958274941762528116445171161040040833357876134689749846940052619392750394683504816081193432350669452446113285638982551762586656329109007214019944975816434827768882704630460001209452239162896576191876324662333153835533956600295255158377025198426950944040643235430211011063586032467724329735785947372051759042138171054165854842472990583800899984893232549092766400510300083585513014171220423103452292891496141806956300396540682381668367564569427813092064053993103537635994311143010708814851867239706492577203899024
n18 = 19591441383958529435598729113936346657001352578357909347657257239777540424811749817783061233235817916560689138344041497732749011519736303038986277394036718790971374656832741054547056417771501234494768509780369075443550907847298246275717420562375114406055733620258777905222169702036494045086017381084272496162770259955811174440490126514747876661317750649488774992348005044389081101686016446219264069971370646319546429782904810063020324704138495608761532563310699753322444871060383693044481932265801505819646998535192083036872551683405766123968487907648980900712118052346174533513978009131757167547595857552370586353973
c18 = 3834917098887202931981968704659119341624432294759361919553937551053499607440333234018189141970246302299385742548278589896033282894981200353270637127213483172182529890495903425649116755901631101665876301799865612717750360089085179142750664603454193642053016384714515855868368723508922271767190285521137785688075622832924829248362774476456232826885801046969384519549385428259591566716890844604696258783639390854153039329480726205147199247183621535172450825979047132495439603840806501254997167051142427157381799890725323765558803808030109468048682252028720241357478614704610089120810367192414352034177484688502364022887
n19 = 19254242571588430171308191757871261075358521158624745702744057556054652332495961196795369630484782930292003238730267396462491733557715379956969694238267908985251699834707734400775311452868924330866502429576951934279223234676654749272932769107390976321208605516299532560054081301829440688796904635446986081691156842271268059970762004259219036753174909942343204432795076377432107630203621754552804124408792358220071862369443201584155711893388877350138023238624566616551246804054720492816226651467017802504094070614892556444425915920269485861799532473383304622064493223627552558344088839860178294589481899206318863310603
c19 = 6790553533991297205804561991225493105312398825187682250780197510784765226429663284220400480563039341938599783346724051076211265663468643826430109013245014035811178295081939958687087477312867720289964506097819762095244479129359998867671811819738196687884696680463458661374310994610760009474264115750204920875527434486437536623589684519411519100170291423367424938566820315486507444202022408003879118465761273916755290898112991525546114191064022991329724370064632569903856189236177894007766690782630247443895358893983735822824243487181851098787271270256780891094405121947631088729917398317652320497765101790132679171889
n20 = 26809700251171279102974962949184411136459372267620535198421449833298448092580497485301953796619185339316064387798092220298630428207556482805739803420279056191194360049651767412572609187680508073074653291350998253938793269214230457117194434853888765303403385824786231859450351212449404870776320297419712486574804794325602760347306432927281716160368830187944940128907971027838510079519466846176106565164730963988892400240063089397720414921398936399927948235195085202171264728816184532651138221862240969655185596628285814057082448321749567943946273776184657698104465062749244327092588237927996419620170254423837876806659
c20 = 386213556608434013769864727123879412041991271528990528548507451210692618986652870424632219424601677524265011043146748309774067894985069288067952546139416819404039688454756044862784630882833496090822568580572859029800646671301748901528132153712913301179254879877441322285914544974519727307311002330350534857867516466612474769753577858660075830592891403551867246057397839688329172530177187042229028685862036140779065771061933528137423019407311473581832405899089709251747002788032002094495379614686544672969073249309703482556386024622814731015767810042969813752548617464974915714425595351940266077021672409858645427346
nList = [n1, n2, n3, n4, n5, n6, n7, n8, n9, n10, n11, n12, n13, n14, n15, n16, n17, n18, n19, n20]
cList = [c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11, c12, c13, c14, c15, c16, c17, c18, c19, c20]
print(solve(nList, cList))
Operation results
The common divisor of n[4] and n[17] is
132585806383798600305426957307612567604223562626764190211333136246643723811046149337852966828729052476725552361132437370521548707664977123165279305052971868012755509160408641100548744046621516877981864180076497524093201404558036301820216274968638825245150755772559259575544101918590311068466601618472464832499
Decompose n[4] to obtain:
22822039733049388110936778173014765663663303811791283234361230649775805923902173438553927805407463106104699773994158375704033093471761387799852168337898526980521753614307899669015931387819927421875316304591521901592823814417756447695701045846773508629371397013053684553042185725059996791532391626429712416994990889693732805181947970071429309599614973772736556299404246424791660679253884940021728846906344198854779191951739719342908761330661910477119933428550774242910420952496929605686154799487839923424336353747442153571678064520763149793294360787821751703543288696726923909670396821551053048035619499706391118145067 =
132585806383798600305426957307612567604223562626764190211333136246643723811046149337852966828729052476725552361132437370521548707664977123165279305052971868012755509160408641100548744046621516877981864180076497524093201404558036301820216274968638825245150755772559259575544101918590311068466601618472464832499 *
172130338499326278748088659642118539903263306644625489813269854049704514120598134934786316771912260248369075948864036229605563950070491992643125838594149381631362120542615545158696925360916086470107987771246645459433841320759048661246016875180635458357799131806734777129141845728102816378815607663660131827433
b'flag{abdcbe5fd94e23b3de429223ab9c2fdf}'
flag
flag{abdcbe5fd94e23b3de429223ab9c2fdf}
[hdctf2019] bbrsa (basic questions)
subject
enc file:
p = 177077389675257695042507998165006460849
n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
c = ==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM
encode (1).py:
from base64 import b64encode as b32encode from gmpy2 import invert,gcd,iroot from Crypto.Util.number import * from binascii import a2b_hex,b2a_hex import random flag = "******************************" nbit = 128 p = getPrime(nbit) q = getPrime(nbit) n = p*q print p print n phi = (p-1)*(q-1) e = random.randint(50000,70000) while True: if gcd(e,phi) == 1: break; else: e -= 1; c = pow(int(b2a_hex(flag),16),e,n) print b32encode(str(c))[::-1] # 2373740699529364991763589324200093466206785561836101840381622237225512234632
Problem solving ideas
Known {p, n, c}, q = n / p
Now, if you want to calculate the decryption private key d, you also need to know the value of e
From the encrypted code, we can see that the range of e is (5000070000). Just blow it up directly
Of course, c goes through base64 and reverse order. First, it should be restored to numbers
Attach Code:
import base64
import gmpy2
import binascii
c = "==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM"
c = int(base64.b64decode(c[::-1])) #base64 decoding + reverse order, restore c
n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
p = 177077389675257695042507998165006460849
q = n // p
phi = (p-1)*(q-1)
for e in range(50000, 70000):
if gmpy2.gcd(e,phi) == 1:
d = gmpy2.invert(e,(p-1)*(q-1)) #Calculate private key d
m = hex(gmpy2.powmod(c, d, n)) #decrypt
if len(m) % 2 == 1: #It is not an entire byte and cannot be converted to text. Skip it directly
continue
flag = str(binascii.unhexlify(m[2:]))
print(flag)
if "flag" in flag or "FLAG" in flag:
print(e)
break
The blasting speed is very fast, e = 51527 gives the result, which is basically seconds
flag
flag{rs4_1s_s1mpl3!#}
[bjdctf2020] RSA (basic questions)
subject
from Crypto.Util.number import getPrime,bytes_to_long
flag=open("flag","rb").read()
p=getPrime(1024)
q=getPrime(1024)
assert(e<100000)
n=p*q
m=bytes_to_long(flag)
c=pow(m,e,n)
print c,n
print pow(294,e,n)
p=getPrime(1024)
n=p*q
m=bytes_to_long("BJD"*32)
c=pow(m,e,n)
print c,n
'''
output:
12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
'''
Problem solving ideas
Two encryptions are performed here, namely:
- Encrypt flag, known {n1, c1}
- Encrypt "BJD"*32, known {n2, c2}
At the same time, pow(294, e, n1) is also known. According to this, the range of E, e can be solved (e < 100000)
Then, in the two encryption, the same large prime factor q is multiplexed
That is, n1 = p1 * q; n2 = p2 * q
Therefore, it is very simple to calculate the common divisor of n1 and n2 to get q, p1 = n1 // q
So far, {n1, p1, q, e, c} is complete
Attach Code:
import base64
import gmpy2
import binascii
c1 = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120
n1 = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
n2 = 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
c0 = 381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
#c0 = pow(294,e,n1)
for e in range(100000):
if gmpy2.powmod(294,e,n1) == c0:
print("e = ", e)
break
q = gmpy2.gcd(n1, n2)
p = n1 // q
d = gmpy2.invert(e,(p-1)*(q-1))
m = gmpy2.powmod(c1, d, n1)
flag = binascii.unhexlify(hex(m)[2:])
print(flag)
Operation results
e = 52361
b'BJD{p_is_common_divisor}'
flag
flag{p_is_common_divisor}
[BJDCTF2020]rsa_ Output (common mode attack)
subject
{21058339337354287847534107544613605305015441090508924094198816691219103399526800112802416383088995253908857460266726925615826895303377801614829364034624475195859997943146305588315939130777450485196290766249612340054354622516207681542973756257677388091926549655162490873849955783768663029138647079874278240867932127196686258800146911620730706734103611833179733264096475286491988063990431085380499075005629807702406676707841324660971173253100956362528346684752959937473852630145893796056675793646430793578265418255919376323796044588559726703858429311784705245069845938316802681575653653770883615525735690306674635167111,2767}
{21058339337354287847534107544613605305015441090508924094198816691219103399526800112802416383088995253908857460266726925615826895303377801614829364034624475195859997943146305588315939130777450485196290766249612340054354622516207681542973756257677388091926549655162490873849955783768663029138647079874278240867932127196686258800146911620730706734103611833179733264096475286491988063990431085380499075005629807702406676707841324660971173253100956362528346684752959937473852630145893796056675793646430793578265418255919376323796044588559726703858429311784705245069845938316802681575653653770883615525735690306674635167111,3659}
message1=20152490165522401747723193966902181151098731763998057421967155300933719378216342043730801302534978403741086887969040721959533190058342762057359432663717825826365444996915469039056428416166173920958243044831404924113442512617599426876141184212121677500371236937127571802891321706587610393639446868836987170301813018218408886968263882123084155607494076330256934285171370758586535415136162861138898728910585138378884530819857478609791126971308624318454905992919405355751492789110009313138417265126117273710813843923143381276204802515910527468883224274829962479636527422350190210717694762908096944600267033351813929448599
message2=11298697323140988812057735324285908480504721454145796535014418738959035245600679947297874517818928181509081545027056523790022598233918011261011973196386395689371526774785582326121959186195586069851592467637819366624044133661016373360885158956955263645614345881350494012328275215821306955212788282617812686548883151066866149060363482958708364726982908798340182288702101023393839781427386537230459436512613047311585875068008210818996941460156589314135010438362447522428206884944952639826677247819066812706835773107059567082822312300721049827013660418610265189288840247186598145741724084351633508492707755206886202876227
Problem solving ideas
Look at the content given. It should be known {n1, e1, c1}, {n2, e2, c2}. Find the plaintext
Note that n1 and n2 are the same here, so they are common mode attacks
Common mode attack means that the same module n is used in the process of generating the secret key. At this time, the same information m is encrypted with different secret keys e1 and e2 to obtain different ciphertexts c1 and c2, i.e
me1 % n = c1
me2 % n = c2
Because e1 and e2 are prime numbers, the extended Euclidean algorithm
s1 and s2 can be calculated so that
e1 * s1 + e2 * s2 = 1
Based on this information, m can be calculated directly
The formula is derived as follows:
m = m % n
m = m1 % n
m = m(e1*s1+e2*s2) % n
m = (me1*s1 % n * me2*s1 % n) % n
m = (c1s1 % n * c2s2 % n) % n
Attach Code:
import gmpy2 import binascii e1 = 2767 e2 = 3659 n = 21058339337354287847534107544613605305015441090508924094198816691219103399526800112802416383088995253908857460266726925615826895303377801614829364034624475195859997943146305588315939130777450485196290766249612340054354622516207681542973756257677388091926549655162490873849955783768663029138647079874278240867932127196686258800146911620730706734103611833179733264096475286491988063990431085380499075005629807702406676707841324660971173253100956362528346684752959937473852630145893796056675793646430793578265418255919376323796044588559726703858429311784705245069845938316802681575653653770883615525735690306674635167111 c1 = 20152490165522401747723193966902181151098731763998057421967155300933719378216342043730801302534978403741086887969040721959533190058342762057359432663717825826365444996915469039056428416166173920958243044831404924113442512617599426876141184212121677500371236937127571802891321706587610393639446868836987170301813018218408886968263882123084155607494076330256934285171370758586535415136162861138898728910585138378884530819857478609791126971308624318454905992919405355751492789110009313138417265126117273710813843923143381276204802515910527468883224274829962479636527422350190210717694762908096944600267033351813929448599 c2 = 11298697323140988812057735324285908480504721454145796535014418738959035245600679947297874517818928181509081545027056523790022598233918011261011973196386395689371526774785582326121959186195586069851592467637819366624044133661016373360885158956955263645614345881350494012328275215821306955212788282617812686548883151066866149060363482958708364726982908798340182288702101023393839781427386537230459436512613047311585875068008210818996941460156589314135010438362447522428206884944952639826677247819066812706835773107059567082822312300721049827013660418610265189288840247186598145741724084351633508492707755206886202876227 #extended euclidean algorithm #return (r,x,y) where r is the greatest common divisor of a and b, and xy satisfies ax + by = 1 r, s1, s2 = gmpy2.gcdext(e1, e2) #Calculate s1, s2 m = (gmpy2.powmod(c1,s1,n)*gmpy2.powmod(c2,s2,n)) % n #Compute plaintext m flag = binascii.unhexlify(hex(m)[2:]) print(flag)
Operation results
b'BJD{r3a_C0mmoN_moD@_4ttack}'
flag
flag{r3a_C0mmoN_moD@_4ttack}
[ACTF freshman competition 2020] crypto-rsa0 (basic RSA + pseudo encryption)
subject
Give challenge Zip to open the discovery prompt, you need to enter a password
Take another look at hint txt:
What should I do? The person who wrote the question was too bad to encrypt the compressed package!
Pseudo encryption??? I thought it was an empty password at first, but after trying, I found that I couldn't enter an empty password
There's no way. It's also a blind area of knowledge. Learn online
Pseudo encryption principle
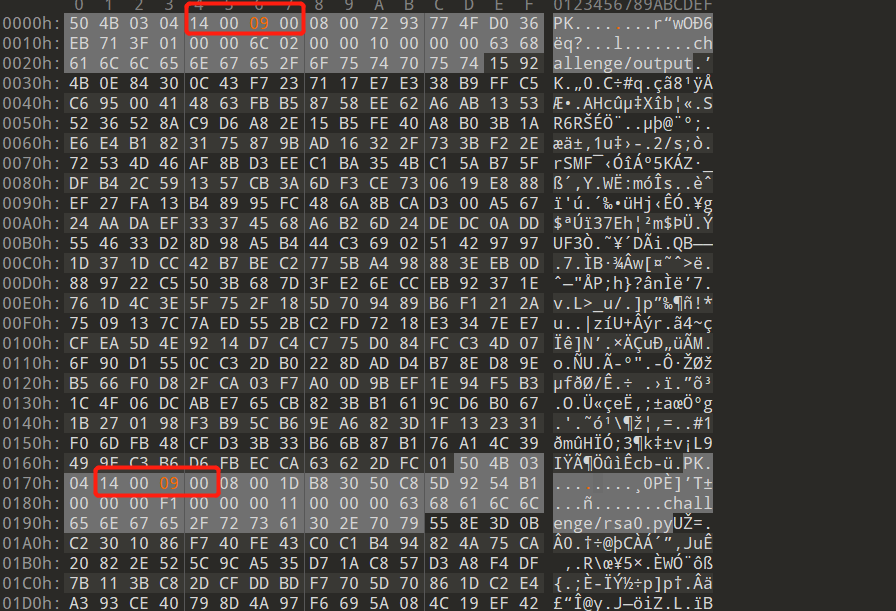
The above is a screenshot of opening the compressed file with 010 editor
A zip file consists of three parts: compressed source file data area + compressed source file directory area + compressed source file directory end flag
Compress source file data area:
50 4B 03 04: This is the header file tag (0x04034b50)
14 00: pkware version required to unzip the file
00: global mode bit mark (with or without encryption)
Compressed source file directory area:
50 4B 01 02: header mark of file in directory (0x02014b50)
3F 00: pkware version used for compression
14 00: pkware version required to unzip the file
00: global mode bit mark (encryption or not, the key of pseudo encryption)
Pay attention to the encryption bit mark of the file header. Pseudo encryption is to convert the unencrypted file into a pseudo encrypted file by modifying the encryption bit
Therefore, find 1400 in all file headers, change the encryption bits after 1400 to 00 00, and the pseudo encrypted file becomes an unencrypted file
Get the output file inside
9018588066434206377240277162476739271386240173088676526295315163990968347022922841299128274551482926490908399237153883494964743436193853978459947060210411
7547005673877738257835729760037765213340036696350766324229143613179932145122130685778504062410137043635958208805698698169847293520149572605026492751740223
50996206925961019415256003394743594106061473865032792073035954925875056079762626648452348856255575840166640519334862690063949316515750256545937498213476286637455803452890781264446030732369871044870359838568618176586206041055000297981733272816089806014400846392307742065559331874972274844992047849472203390350
Rsa0 py
from Cryptodome.Util.number import * import random FLAG=#hidden, please solve it flag=int.from_bytes(FLAG,byteorder = 'big') p=getPrime(512) q=getPrime(512) print(p) print(q) N=p*q e=65537 enc = pow(flag,e,N) print (enc)
It is known that {p, q, e, c} is a basic problem. Solve it directly
Attach Code:
import gmpy2 import binascii e = 65537 p = 9018588066434206377240277162476739271386240173088676526295315163990968347022922841299128274551482926490908399237153883494964743436193853978459947060210411 q = 7547005673877738257835729760037765213340036696350766324229143613179932145122130685778504062410137043635958208805698698169847293520149572605026492751740223 c = 50996206925961019415256003394743594106061473865032792073035954925875056079762626648452348856255575840166640519334862690063949316515750256545937498213476286637455803452890781264446030732369871044870359838568618176586206041055000297981733272816089806014400846392307742065559331874972274844992047849472203390350 n = p * q d = gmpy2.invert(e,(p-1)*(q-1)) m = gmpy2.powmod(c, d, n) flag = binascii.unhexlify(hex(m)[2:]) print(flag)
Operation results
b'actf{n0w_y0u_see_RSA}'
flag
flag{n0w_y0u_see_RSA}
[gwctf 2019] babyrsa (basic RSA + solution equation)
subject
secret:
N=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163 m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239 m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546
encrypt.py:
import hashlib
import sympy
from Crypto.Util.number import *
flag = 'GWHT{******}'
secret = '******'
assert(len(flag) == 38)
half = len(flag) / 2
flag1 = flag[:half]
flag2 = flag[half:]
secret_num = getPrime(1024) * bytes_to_long(secret)
p = sympy.nextprime(secret_num)
q = sympy.nextprime(p)
N = p * q
e = 0x10001
F1 = bytes_to_long(flag1)
F2 = bytes_to_long(flag2)
c1 = F1 + F2
c2 = pow(F1, 3) + pow(F2, 3)
assert(c2 < N)
m1 = pow(c1, e, N)
m2 = pow(c2, e, N)
output = open('secret', 'w')
output.write('N=' + str(N) + '\n')
output.write('m1=' + str(m1) + '\n')
output.write('m2=' + str(m2) + '\n')
output.close()
Problem solving ideas
Given {n, e, m1, m2} (where m refers to the output ciphertext), solve the plaintext
Let's look at the encryption code first. The flag is divided into two parts F1 and F2.
Then let c1 = F1 + F2 (where f is a long integer and c1 is an arithmetic addition), c2 = pow(F1, 3) + pow(F2, 3)
Then encrypt m1 and m2 with RSA
RSA module n can be directly decomposed on the website, so it doesn't take much effort
After obtaining p and q, it is natural to decrypt and calculate c1 and c2
The latter problem is to solve a simple bivariate cubic function:
F1 + F2 = c1
F13 + F23 = c2
The solution formula derived here is:
Let t = (c13 - c2)/(3*c1)
F1 = c1+sqrt(c12-4t)/2
F2 = c1 - F1
Attach Code:
import math import gmpy2 import binascii n = 636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163 m1 = 90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239 m2 = 487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546 p = 797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377747699 q = 797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377748737 e = 65537 d = gmpy2.invert(e,(p-1)*(q-1)) c1 = gmpy2.powmod(m1, d, n) #c1 = F1 + F2 c2 = gmpy2.powmod(m2, d, n) #c2 = pow(F1, 3) + pow(F2, 3) t = ((c1**3)-c2)//(3*c1) F1 = (c1+gmpy2.iroot(c1**2-4*t,2)[0])//2 F2 = c1 - F1 f1 = binascii.unhexlify(hex(F1)[2:]) f2 = binascii.unhexlify(hex(F2)[2:]) print(f1+f2)
When solving, it should be noted that math cannot be used for square root Sqrt instead of gmpy2 Iroot, the former will have obvious errors in calculating large numbers
Operation results
b'GWHT{f709e0e2cfe7e530ca8972959a1033b2}'
flag
flag{f709e0e2cfe7e530ca8972959a1033b2}
Samemod (common mode attack)
subject
{6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249,773}
{6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249,839}
message1=3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
message2=5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535
Problem solving ideas
The hint is very obvious. SameMod has the same modulus, that is, common mode attack
Look at the content given. We know {n1, e1, c1}, {n2, e2, c2}, and here n1 = n2, find the plaintext
For the principle of common mode attack, see the question above: BJDCTF2020rsa_output
Attach Code:
import gmpy2
import binascii
e1 = 773
e2 = 839
n = 6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249
c1 = 3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
c2 = 5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535
#extended euclidean algorithm
#return (r,x,y) where r is the greatest common divisor of a and b, and xy satisfies ax + by = 1
r, s1, s2 = gmpy2.gcdext(e1, e2) #Calculate s1, s2
m = (gmpy2.powmod(c1,s1,n)*gmpy2.powmod(c2,s2,n)) % n #Compute plaintext m
print(m)
mStr = str(m)
i, flag = 0, ''
while i < len(mStr):
if mStr[i] == '1':
flag += chr(int(mStr[i:i+3]))
i += 3
else:
flag += chr(int(mStr[i:i+2]))
i += 2
print(flag)
Operation results
1021089710312311910410111011910111610410511010710511610511511211111511510598108101125
flag{whenwethinkitispossible}
Another point to note is that the hexadecimal to Ascll text is generally calculated after the plaintext.
However, this problem is special. It is a decimal to ascll code. Pay attention to distinguish whether the ascll value is two or three digits
flag
flag{whenwethinkitispossible}
[wustctf2020] babyrsa (basic question)
subject
c = 28767758880940662779934612526152562406674613203406706867456395986985664083182 n = 73069886771625642807435783661014062604264768481735145873508846925735521695159 e = 65537
Problem solving ideas
A check-in question, known {n, e, c}, to solve the plaintext
Take n to decompose and then calculate the private key d to decrypt. There's nothing to say
Factorization website factordb.com
Operation results
b'wctf2020{just_@_piece_0f_cak3}'
flag
flag{just_@_piece_0f_cak3}