Definition
The so-called shortest path problem refers to: if there may be more than one path from one vertex (source point) to another vertex (end point) in the graph, how to find a path to minimize the sum of weights (called path length) along each side of the path.
Next, we introduce two commonly used shortest path algorithms:
Dijkstra algorithm
His algorithm idea is to merge step by step according to the increasing order of path length, which is an application of greedy algorithm to solve the shortest path problem from single source point to other vertices.
Algorithmic thought
First, we introduce an auxiliary vector D, each component D[i] of which represents the length of the shortest path currently found from the start node V to the end node vi. Its initial state is: if there is an arc from node V to node V I, then D[i] is the weight on the arc, otherwise D[i] is ∞, obviously, the path with length D[j] = Min{D[i] | vi ∈ V} is the shortest path starting from V, and the path is (v, vi).
So, which is the next shortest path? If the end point of the sub short path is vk, we can imagine that this path is either (v, vk) or (v, vj, vk). Its length is either the weight on the arc from v to vk, or the sum of D[j] and the weight from vj to vk.
So the length of the next shortest path is: D[j] = Min{D[i] | vi ∈ V - S}, where D[i] is either the weight of the arc (v, vi), or D k And the sum of the weights on the arc (vk, vi).
Algorithm description
It is assumed that the shortest path between vertex V0 and other vertices as shown in the following example figure is required:
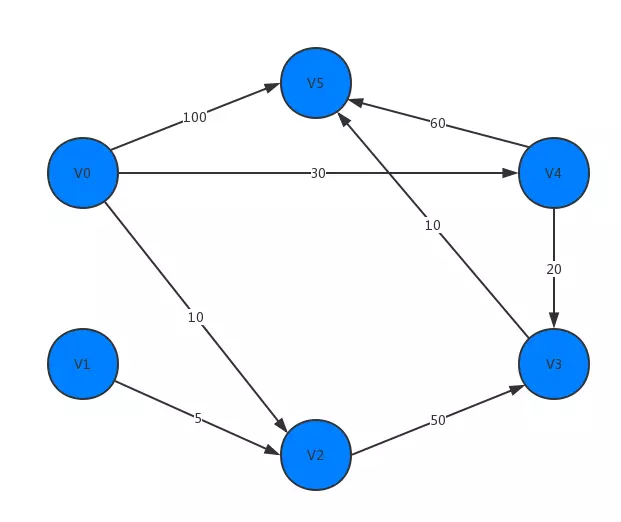
We use Guava's ValueGraph as the data structure of the graph. Each vertex corresponds to a visited variable to indicate whether the node is in V or S. initially, there is only vertex V0 in S. Then, let's see whether the newly added vertices can reach other vertices, and whether the path length to reach other points through this vertex is shorter than that from V0 directly. If so, modify the weights of these vertices (that is, if (d [J] + arcs [J] [k] < D [k]) then d [k] = D [J] + arcs [J] [k]). Then find the minimum value from {V - S} and repeat the above action until all vertices are incorporated into S.
In the first step, we construct an instance of the graph through ValueGraphBuilder, and input the edge set:
MutableValueGraph<String, Integer> graph = ValueGraphBuilder.directed()
.nodeOrder(ElementOrder.insertion())
.expectedNodeCount(10)
.build();
graph.putEdgeValue(V0, V2, 10);
graph.putEdgeValue(V0, V4, 30);
graph.putEdgeValue(V0, V5, 100);
graph.putEdgeValue(V1, V2, 5);
graph.putEdgeValue(V2, V3, 50);
graph.putEdgeValue(V3, V5, 10);
graph.putEdgeValue(V4, V3, 20);
graph.putEdgeValue(V4, V5, 60);
return graph;The initial output is as follows:
nodes: [v0, v2, v4, v5, v1, v3],
edges: {<v0 -> v5>=100, <v0 -> v4>=30, <v0 -> v2>=10,
<v2 -> v3>=50, <v4 -> v5>=60, <v4 -> v3>=20, <v1 -> v2>=5,
<v3 -> v5>=10}In order not to destroy the graph state, we introduce a temporary structure to record the intermediate results of each node operation:
private static class NodeExtra {
public String nodeName; //Current node name
public int distance; //Shortest path from start point to current node
public boolean visited; //The shortest path (S set) that the current node has evaluated
public String preNode; //Previous node name
public String path; //All path points of the path
}In the second step, we first merge the starting point V0 into the set S, because its shortest path is known as 0:
startNode = V0; NodeExtra current = nodeExtras.get(startNode); current.distance = 0; //The shortest path that can be set to start node at the beginning is 0 current.visited = true; //Merge into S set current.path = startNode; current.preNode = startNode;
Step 3: find out the node with the shortest path from the start point V0 to other nodes in the current state:
NodeExtra minExtra = null; //Node information with the shortest path
int min = Integer.MAX_VALUE;
for (String notVisitedNode : nodes) {
//Get auxiliary information of node
NodeExtra extra = nodeExtras.get(notVisitedNode);
//Not in S set and path is short
if (!extra.visited && extra.distance < min) {
min = extra.distance;
minExtra = extra;
}
}The fourth step is to merge the nodes with the shortest path into the set S:
if (minExtra != null) { //The node with the shortest path was found
minExtra.visited = true; //Merge into set S
//Update node path
minExtra.path = nodeExtras.get(minExtra.preNode).path + " -> " + minExtra.nodeName;
current = minExtra; //Identifies the shortest path node currently incorporated
}Step 5: update the intermediate result of the shortest path of its related nodes:
/**
* After merging the nodes found in the new query, update the intermediate result of the shortest path of the related nodes
* if (D[j] + arcs[j][k] < D[k]) D[k] = D[j] + arcs[j][k]
*/
//Just loop through the successor list of the current node (optimization)
Set<String> successors = graph.successors(current.nodeName);
for (String notVisitedNode : successors) {
NodeExtra extra = nodeExtras.get(notVisitedNode);
if (!extra.visited) {
final int value = current.distance
+ graph.edgeValueOrDefault(current.nodeName,
notVisitedNode, 0); //D[j] + arcs[j][k]
if (value < extra.distance) { //D[j] + arcs[j][k] < D[k]
extra.distance = value;
extra.preNode = current.nodeName;
}
}
}Step 6: output the shortest path from the start node V0 to each node and the path point information
Set<String> keys = nodeExtras.keySet();
for (String node : keys) {
NodeExtra extra = nodeExtras.get(node);
if (extra.distance < Integer.MAX_VALUE) {
Log.i(TAG, startNode + " -> " + node + ": min: " + extra.distance
+ ", path: " + extra.path); //path updated during operation
}
}The output result of the example diagram is:
v0 -> v0: min: 0, path: v0 v0 -> v2: min: 10, path: v0 -> v2 v0 -> v3: min: 50, path: v0 -> v4 -> v3 v0 -> v4: min: 30, path: v0 -> v4 v0 -> v5: min: 60, path: v0 -> v4 -> v3 -> v5
For example demo implementation of Dijkstra algorithm, please refer to: