Learning materials related to this training:
Euler function -- the number of Coprime numbers with N in numbers less than n
Game theory and algorithm implementation (three basic games)
Fast power (Java implementation code)
catalogue
H - number of Coprime numbers (I)
I - Sumdiv (not done)
K - combinatorial number problem
A - A^B Mod C
Give three positive integers a, B, C and find A^B Mod C.
For example, 3 5 8, 3^5 Mod 8 = 3.
Input
Three positive integers a, B, C, separated by spaces. (1 <= A,B,C <= 10^9)
Output
Output calculation results
Sample Input
3 5 8
Sample Output
3
Solution: (fast power) the power b of a increases exponentially and easily exceeds the long type, so we need to take the module after each multiplication
import java.util.*;
public class Test01 {
public static void main(String [] args) {
Scanner cin=new Scanner(System.in);
long a=cin.nextLong();
long b=cin.nextLong();
long c=cin.nextLong();
System.out.println(mpow(a,b,c)%c);
}
/*
a Modulo c to the power of b
Because the power b of a increases exponentially and easily exceeds the long type, we need to take the module after each multiplication
(a+b)%c--->((a%c) + (b%c)) %c (a*b)%c--->((a%c) * (b%c)) %c
*/
static long mpow(long a,long b,long c) {//Fast power finding a^b%p
long s=(long)1;
while(b!=0) {
if((b&1)==1) s=s*a%c;
a=a*a%c;
b=b/2;//The binary number equivalent to b is shifted one bit to the right
}
return s;
}
}
B - inverse element
Akkeshi is the leader of the general mobilization for marriage proposal. Through his own hands, he has achieved the dreams of countless young people, but he has left sad tears.
Proposing marriage is very laborious. He has p − 1 proposal request in his hand, and the number of this # ii individual is [1,P − 1]
Facing the , i , individual, his proposal trouble value is: the inverse element of i , in the sense of module , P ,.
He now wants to know the total trouble value.
tips: if any number , i , has no inverse element in the sense of module , P , please output AKCniubi
Input format
One number per line , P , represents the total number of marriage proposals
Output format
One number per line represents the total trouble value
If there is no inverse element, output AKCniubi
Data range
For 30% of data, P < = 1000000
For 50% of data, P < = 10000000
For 100% data, P < = 231
Sample Input
3
Sample Output
3
Solution: according to the meaning of the question, you can judge whether P is a prime number. If it is a prime number, you can directly sum the result through the sequence of equal differences. If it is not a prime number, you can output "AKCniubi"
import java.util.Scanner;
public class Test02 {
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
/*
When ax ≡ 1(modb), x is the inverse of a in the sense of mod b.
In short, the inverse element is the reciprocal of a number in the sense of mod. For example, 5x ≡ 1 (mod3), x=2 satisfies 10 = 1 (mod3), so 2 is the inverse element of 5 in the sense of mod3
*/
long p=cin.nextLong();
if (check(p)){//Judge whether it is a prime number. If it is a prime number, directly call the summation formula of the equal difference sequence to calculate the result
System.out.println(p*(p-1)/2);
}else {
System.out.println("AKCniubi");
}
}
static boolean check(long p) {//Judge whether it is a prime number
for (int i=2;i*i<=p;i++){
if (p%i==0){
return false;
}
}
return true;
}
}
C - number of decision primes
Enter two integers x and Y, and output the number of primes (including X and Y) between - > >.
Input
Two integers X and Y (1 < = X, y < = 105).
Output
Output an integer representing the number of primes between X and Y (including X and y).
Sample Input
1 100
Sample Output
25
Problem solution: enumerate the numbers between X and y, and the constructor can judge whether each number is a prime number
import java.util.Scanner;
public class Test03 {
public static void main(String[] args) {
Scanner cin=new Scanner(System.in);
int X=cin.nextInt();
int Y=cin.nextInt();
int count=0;
//Just enumerate the numbers between X and y
if (X<Y){
for (int i=X;i<=Y;i++){
if (check(i)){
count++;
}
}
}else {
for (int i=Y;i<=X;i++){
if (check(i)){
count++;
}
}
}
System.out.println(count);
}
static boolean check(int i) {//Judge whether it is prime
if (i==1){
return false;
}
for(int j=2;j*j<=i;j++) {
if(i%j==0)
return false;
}
return true;
}
}
D - matrix multiplication
Calculate the multiplication of two matrices. n × Matrix A of order m times M × The matrix C obtained from the matrix B of order k is n × Of order k, and C[i][j]=A[i][0] × B[0][j]+A[i][1] × B[1][j]+……+A[i][m−1] × B[m − 1][j](C[i][j] represents the element in the − I − th row and − J − th column of the − C − matrix).
Input format
The first row, n,m,k, indicates that the A ^ matrix is n ^ row ^ column, the B ^ matrix is n ^ row ^ column, and n,m,k ^ are all less than ^ 100;
Then input the two matrices A ^ A ^ and B ^ successively. The absolute value of each element in the matrix will not be greater than 1000.
Output format
The output matrix , C, a total of , n , rows, k , integers in each row, separated by a space.
Sample Input
3 2 3 1 1 1 1 1 1 1 1 1 1 1 1
Sample Output
2 2 2 2 2 2 2 2 2
Solution: according to the definition of matrix multiplication, obtain the C matrix (A*B) and output it
import java.util.Scanner;
public class Test04 {
public static void main(String[] args) {
Scanner cin=new Scanner(System.in);
int n=cin.nextInt();
int m=cin.nextInt();
int k=cin.nextInt();
int A[][]=new int[n][m];
int B[][]=new int[m][k];
int C[][]=new int[n][k];
for (int i=0;i<n;i++){
for (int j=0;j<m;j++){
A[i][j]=cin.nextInt();
}
}
for (int j=0;j<m;j++){
for (int q=0;q<k;q++){
B[j][q]=cin.nextInt();
}
}
for (int i=0;i<n;i++){
for (int j=0;j<m;j++){
for (int q=0;q<k;q++){
C[i][q]+=(A[i][j]*B[j][q]);
}
}
}
for (int i=0;i<n;i++){
for (int j=0;j<k;j++){
System.out.print(C[i][j]+" ");
}
System.out.println();
}
}
}
E - Bash games
There is a pile of stones, a total of N. A and B take turns. A takes it first. Take at least one stone at a time and K at most. The one who gets the last stone wins. Suppose a and B are very smart, and there will be no mistakes in the process of taking stones. Give N and K and ask who can win the game in the end.
For example, N = 3, K = 2. No matter how A takes it, B can get the last stone.
Input
Line 1: a number T, indicating the number of numbers to be used as input tests later. (1 < = T < = 10000) line 2 - T + 1: 2 numbers n, K per line. The middle is separated by a space. (1 <= N,K <= 10^9)
Output
A total of T lines, if a wins, output a, if B wins, output B.
Sample Input
4 3 2 4 2 7 3 8 3
Sample Output
B A A B
Solution: typical Bash Game
import java.util.Scanner;
public class Test05 {
public static void main(String[] args) {//Bash Game
/*
Bash game
There is only a pile of n items. Two people take turns to take items from this pile. It is stipulated that at least one item shall be taken each time, and at most m items shall be taken.
(1)The last light winner:
If n%(m+1)==0, the second hand will win, otherwise the first hand will win.
(2)Last light takers:
If (n-1)%(m+1)==0, the second hand will win, otherwise the first hand will win.
*/
Scanner cin=new Scanner(System.in);
int T=cin.nextInt();
while (T-->0){
int N=cin.nextInt();
int K=cin.nextInt();
if (N%(K+1)==0){
System.out.println("B");
}else {
System.out.println("A");
}
}
}
}
F - stone game
There are two piles of stones in any number, which can be different. At the beginning of the game, two people take turns to take stones. The game stipulates that there are two different ways to take stones each time. One is to take any number of stones from any pile; Second, the same number of stones can be taken from the two piles at the same time. Finally, the winner is the one who takes all the stones. Now give the initial number of two piles of stones. If it's your turn to take first, suppose both sides adopt the best strategy, and ask whether you are the winner or the loser in the end.
Input
The input contains several lines, indicating the initial conditions of several kinds of stones. Each line contains two non negative integers a and b, indicating the number of two piles of stones. A and b are not greater than 1000000000.
Output
There are also several lines corresponding to the output. Each line contains a number 1 or 0. If you are the winner in the end, it is 1, otherwise, it is 0.
Sample Input
2 1 8 4 4 7
Sample Output
0 1 0
Solution: typical wythoff's game
import java.util.Scanner;
public class Test06 {
public static void main(String[] args) {//Wythoff's game
Scanner cin=new Scanner(System.in);
/*
Wythoff's game:
There are two piles of several items, and two people take at least one from any pile in turn or from both piles at the same time
Take out the same number of items and stipulate to take at least one at a time, at most unlimited. Finally, the light taker wins.
Question making ideas:
Let one pile be a and one pile be b, and a is the pile with less items and b is the pile with more items.
If (b-a)*1.618==a, the backhand will win; Or we'll win first.
Since some topics require high accuracy, 1.618 needs to be replaced by ((Math.sqrt(5.0)+1.0)/2.0)// Remember to use math Floor() rounds it up
(Note: the question about the type of wizov game is not necessarily two piles, but can also take the target item, and the target item is placed up and down, that is, one pile, but it can be transformed into two piles up and down, and the target item is the target point for the last light.)
*/
while (cin.hasNext()){
int a=cin.nextInt();
int b=cin.nextInt();
double x=((Math.sqrt(5.0)+1.0)/2.0);
if (a>b){
if (Math.floor((a-b)*x)==b){
System.out.println("0");
}else {
System.out.println("1");
}
}else {
if (Math.floor((b-a)*x)==a){
System.out.println("0");
}else {
System.out.println("1");
}
}
}
}
}
G - Matches Game
This is a simple game. In this game, there are several piles of matches and two players. The two players take turns. In each round, players can select a pile and take out any number of matches from the pile (of course, the number of matches taken out cannot be zero or greater than the number of matches in the selected pile). If a player takes matches and there are no matches left, the player is the winner. It is assumed that both players will make the best decision. Your job is to judge whether the first player can win the game.
Input
The input consists of several lines, each with a test case. At the beginning of a line, there is an integer M (1 < = M < = 20), which is the number of matchstacks. Then M positive integers no greater than 10000000. These M integers represent the number of matches in each stack.
Output
For each test case, if the first player wins, output "Yes" in one line, otherwise output "No".
Sample Input
2 45 45 3 3 6 9
Sample Output
No Yes
Solution: typical nimm game
import java.util.Scanner;
public class Test07 {
public static void main(String[] args) {
/*
Nimm game:
There are three piles of several items, and two people take any number of items from a pile in turn. It is stipulated that at least one item shall be taken at a time, whichever is more, and the one who takes light at last wins.
Nim game model can be extended to: there are n piles of several items, two people take any number of items from a pile in turn, and it is stipulated that at least one item is taken at a time, the more is unlimited, and the one who takes the light wins at last.
The variables in this game are the number of stacks k and the number of items N1, N2,..., Nk in each stack. The corresponding combinatorial problem is to determine whether the first hand wins or the second hand wins, and how the two players should take items to ensure their own victory
Solution: there are n piles of several items. Two people take any number of items from a pile in turn (or at most m, just take each pile of% m). It is required to take at least one item at a time. The more is unlimited. Finally, the one who takes all the items wins.
If the quantity of each stack is different or a1^a2 ^... ^ ai '^... ^ an, and the result is zero, you must lose first, otherwise you must win
*/
Scanner cin=new Scanner(System.in);
while (cin.hasNext()){
int M=cin.nextInt();
int s=0;
for (int i=0;i<M;i++){
int a=cin.nextInt();
s^=a;
}
if (s==0){
System.out.println("No");
}else {
System.out.println("Yes");
}
}
}
}
H - number of Coprime numbers (I)
Here we define φ (n) Represents the number of all coprime numbers less than or equal to n ^ and N ^ n.
For example φ (10) = 4, because we can find 1,3,7,9 and 10 coprime in 1 ∼ 10.
Input format
In the first line, enter an integer, {t, indicating the number of test data groups.
Next, there are lines , t , and each line has an integer , n.
Output format
For each set of test data output φ (n) .
Data range
1≤t≤100,1≤n≤1010.
Sample Input
3 2 10 100
Sample Output
1 4 40
Solution: just delete the number of numbers that can be divided by n, that is, the number of Coprime numbers
import java.util.Scanner;
public class Test08 {
public static void main(String[] args) {
Scanner cin=new Scanner(System.in);
int t= cin.nextInt();
while (t-->0){
long n=cin.nextLong();
long ans=n;
for (long i=2;i*i<=n;i++){
if (n%i==0){
ans=ans/i*(i-1);
while (n%i==0)
n/=i;
}
}
if (n>1){
ans=ans/n*(n-1);
}
System.out.println(ans);
}
}
}
I - Sumdiv
Title Description
There are two natural numbers a and b(a,b ≤ 50000000)
Find the sum module 9901 of all divisors to the power b of a
Input format
A line containing two natural numbers a and b separated by spaces
Output format
A row, divisor of a to the power of b and module 9901
sample input
2 3
sample output
15
Example explanation
The divisor of 8 is 1,2,4,8, and their sum is 15
15 module 9901 is 15
J - The Lottery
Title Description
Give the number of N, m, and m, a[1]... a[m].
Find the number of numbers in 1 * n that are not divided by any one of a[1]... a[m].
10⩽n<2^31,1⩽m⩽15
Input format
Each group of data takes n,m as the first row.
The number of m in the second line represents a[i].
The input file ends with EOF.
Output format
A number on each row of data represents the answer.
sample input
10 2
2 3
20 2
2 4
sample output
3
10
Solution: find out the number of all divisible, n- the number is the answer
import java.util.Scanner;
public class Test11 {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner cin=new Scanner(System.in);
while(cin.hasNext()) {
int n=cin.nextInt();
int m=cin.nextInt();
int p[]=new int[m];
for(int i=0;i<m;i++) {
p[i]=cin.nextInt();
}
int ans=0;
for(int i=1;i<(1<<m);i++) {
long t=1,cnt=0;
for(int j=0;j<m;j++) {
if((i>>j&1)!=0) {
t=lcm(t,p[j]);
if(t>n){
break;
}cnt++;
}
}
if(cnt%2!=0){
ans+=n/t;
}
else {
ans-=n/t;
}
}
System.out.println(n-ans);
}
}
private static long lcm(long t, long i) {
// TODO Auto-generated method stub
// System.out.println(gcd(t,i));
return (long) (t/gcd(t,i)*i);
}
private static long gcd(long t, long l) {
// TODO Auto-generated method stub
if(l==0)return t;
return gcd(l,t%l);
}
}K - combinatorial number problem
The combination number Cnm ^ represents the number of schemes for selecting ^ m ^ items from ^ n ^ items. For example, selecting two items from three items (1,2,3) can have three selection methods (1,2), (1,3), (2,3). According to the definition of combination number, we can give a general formula for calculating combination number:
Cnm=m!(n−m)!n!
Where n= one × two × ⋯ × n.
Shallot wants to know how many pairs (i,j) satisfy Cij for all 0 ≤ i ≤ n, 0 ≤ j ≤ min(i,m) if given n,m ^ and ^ k.
Input format
There are two integers T and k in the first line, where ¢ t ¢ represents the total number of groups of test data k ¢ at the test point. See the title description for the meaning of ¢ k.
Next, there are two integers n,m in each line, and the meaning of n,m is shown in the title description.
Output format
An integer in each row represents how many pairs (i,j) of all 0 ≤ i ≤ n,0 ≤ j ≤ min(i,m) satisfy Cij , which is a multiple of , k ,.
Data range
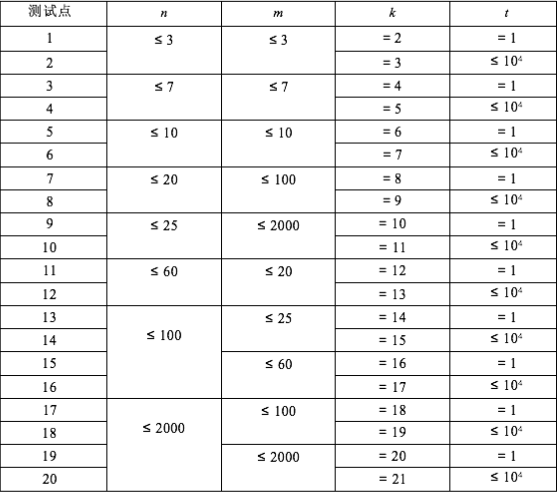
Example description
Example 1:
In all possible cases, only C21 = 2 is a multiple of 2.
Sample Input
1 2 3 3
Sample Output
1
Sample Input 2
2 5 4 5 6 7
Sample Output 2
0 7
Problem solving: find out the number of combinations that meet the meaning of the problem and output it
import java.util.Scanner;
public class Test11 {
public static void main(String[] args) {
int a[][]=new int[2010][2010];
int b[][]=new int [2010][2010];
int n,m,ans,t,k;
Scanner scanner=new Scanner(System.in);
t=scanner.nextInt();
k=scanner.nextInt();
a[1][1]=1%k;
if (a[1][1]==0)
b[1][1]++;
for (int j=2;j<=2001;j++)
{
for (int q=1;q<=Math.min(j,2001);q++)
{
if (q==1)
a[j][q]=(a[j-1][q]+1)%k;
else
a[j][q]=(a[j-1][q]+a[j-1][q-1])%k;
if (a[j][q]==0)
b[j][q]=b[j][q-1]+1;
else
b[j][q]=b[j][q-1];
}
}
for (int i=1;i<=t;i++)
{
n=scanner.nextInt();
m=scanner.nextInt();
ans=0;
for (int j=1;j<=n;j++)
ans+=b[j][Math.min(m,j)];
System.out.println(ans);
}
}
}L - congruence equation
Find the minimum positive integer solution of the congruence equation ax ≡ 1(modb) about ≡ x ≡.
Input format
The input has only one line, containing two positive integers a and B, separated by a space.
Output format
The output has only one line and contains a positive integer x0, the minimum positive integer solution. The input data is guaranteed to have a solution.
Data range
For 40% data, 2 ≤ b ≤ 1000;
For 60% of data, 2 ≤ b ≤ 50000000;
For 100% data, 2 ≤ a,b ≤ 2000000000.
Sample Input
3 10
Sample Output
7
Using the extended Euclidean algorithm to find the inverse of a in the sense of module b
import java.util.Scanner;
public class Test12 {
static long x=0;
static long y=0;
public static void main(String[] args) {
Scanner cin=new Scanner(System.in);
/*
When ax ≡ 1(modb), x is the inverse of a in the sense of mod b.
In short, the inverse element is the reciprocal of a number in the sense of mod. For example, 5x ≡ 1 (mod3), x=2 satisfies 10 = 1 (mod3), so 2 is the inverse element of 5 in the sense of mod3
*/
long a=cin.nextLong();
long b=cin.nextLong();
if (1%(exgcd(a,b))==0){
while (x<=0){
x+=b;
y-=a;
}
System.out.println(x);
}
}
static long exgcd(long a, long b) {
if (b==0){
x=1;
y=0;
return a;
}
long result=exgcd(b,a%b);
long temp=x;
x=y;
y=temp-a/b*y;
return result;
}
}