catalogue
Inheritance structure of Treemap
Treemap underlying data structure
The time complexity of Treemap and why red black tree is selected
LinkedHashMap underlying structure
How does LinkedHashMap maintain order
put,newNode,afterNodeAccess,afterInsertion
Treemap
Introduction to Treemap
In the Map collection framework, in addition to HashMap, TreeMap is also one of the collection objects commonly used in our work.
Compared with HashMap, TreeMap is a Map collection that can compare the size of elements and sort the size of the incoming key s. Among them, you can use the natural order of elements or the custom comparator in the collection to sort;
Different from HashMap's hash mapping, TreeMap implements a tree structure at the bottom. As for the specific form, you can simply understand it as an inverted tree with roots at the top and leaves at the bottom. In computer terms, TreeMap implements the structure of red black tree and forms a binary tree.
TreeMap has the following characteristics:
Duplicate key s are not allowed
Can insert null key, null value
Elements can be sorted. By default, they are sorted by the natural order of Key values
Unordered collection (inconsistent insertion and traversal order)
The clonable interface is implemented, which can be cloned, and the Serializable interface is implemented, which can be serialized
Inheritance structure of Treemap
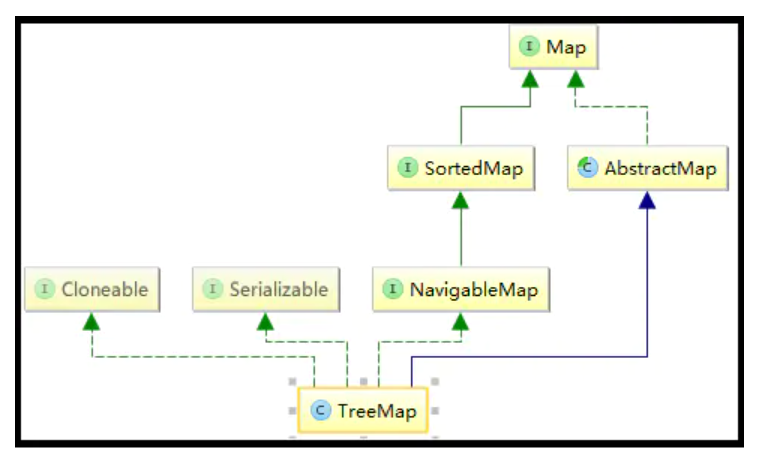
TreeMap inherits from AbstractMap and implements map, Cloneable, navigablemap and serializable interfaces.
(1)TreeMap inherits from AbstractMap, which implements the Map interface and the methods defined in the Map interface, reducing the complexity of its subclass inheritance;
(2)TreeMap implements the Map interface and becomes a member of the Map framework, which can contain elements in the form of key--value;
(3)TreeMap implements NavigableMap interface, which means it has stronger element search ability;
(4)TreeMap implements Cloneable interface and clone() method, which can be cloned;
(5)TreeMap implements Java io. Serializable interface, which supports serialization operation and can be transmitted through Hessian protocol;
NavigableMap and SortedMap
We are familiar with clonable and serializable. Basically, each class in the Java collection framework implements these two interfaces. What does the NavigableMap interface do and what functions does it define? Next, let's look at the source code of NavigableMap!
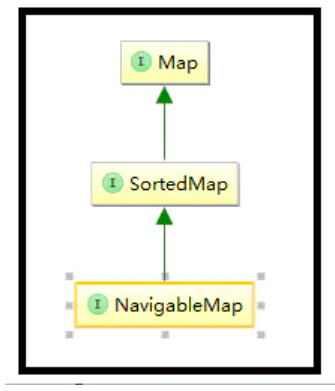
According to the screenshot above, we first introduce the SortedMap interface in the NavigableMap system:
For SortedMap, this class is the parent interface in the TreeMap system and the most critical interface different from the HashMap system.
The main reason is that the first method defined in the SortedMap interface - comparator <? super K> comparator();
This method determines the trend of the TreeMap system. With a comparator, the inserted elements can be sorted;
public interface SortedMap<K,V> extends Map<K,V> {
//Returns the element comparator. If it is a natural order, null is returned;
Comparator<? super K> comparator();
//Returns the set from fromKey to toKey: including header but not tail
java.util.SortedMap<K,V> subMap(K fromKey, K toKey);
//Returns the set from the beginning to toKey: does not contain toKey
java.util.SortedMap<K,V> headMap(K toKey);
//Return the collection from fromKey to the end: including fromKey
java.util.SortedMap<K,V> tailMap(K fromKey);
//Returns the first element in the collection:
K firstKey();
//Returns the last element in the collection:
K lastKey();
//Return the set of all key s in the set:
Set<K> keySet();
//Returns a collection of all value s in the collection:
Collection<V> values();
//Returns the element mapping in the collection:
Set<Map.Entry<K, V>> entrySet();
}The SortedMap interface is introduced above, and the NavigableMap interface is a further extension of SortedMap: it mainly increases the search and acquisition operations of elements in the set, such as returning elements in a certain interval in the set, returning elements less than or greater than a certain value and other similar operations.
public interface NavigableMap<K,V> extends SortedMap<K,V> {
//Return the first element less than key:
Map.Entry<K,V> lowerEntry(K key);
//Return the first key less than key:
K lowerKey(K key);
//Return the first element less than or equal to key:
Map.Entry<K,V> floorEntry(K key);
//Return the first key less than or equal to key:
K floorKey(K key);
//Return the first element greater than or equal to key:
Map.Entry<K,V> ceilingEntry(K key);
//Return the first key greater than or equal to key:
K ceilingKey(K key);
//Return the first element greater than key:
Map.Entry<K,V> higherEntry(K key);
//Return the first key greater than key:
K higherKey(K key);
//Returns the first element in the collection:
Map.Entry<K,V> firstEntry();
//Returns the last element in the collection:
Map.Entry<K,V> lastEntry();
//Returns the first element in the collection and deletes it from the collection:
Map.Entry<K,V> pollFirstEntry();
//Returns the last element in the collection and deletes it from the collection:
Map.Entry<K,V> pollLastEntry();
//Return the Map collection in reverse order:
java.util.NavigableMap<K,V> descendingMap();
NavigableSet<K> navigableKeySet();
//Return the Set set composed of keys in reverse order in the Map Set:
NavigableSet<K> descendingKeySet();
java.util.NavigableMap<K,V> subMap(K fromKey, boolean fromInclusive,
K toKey, boolean toInclusive);
java.util.NavigableMap<K,V> headMap(K toKey, boolean inclusive);
java.util.NavigableMap<K,V> tailMap(K fromKey, boolean inclusive);
SortedMap<K,V> subMap(K fromKey, K toKey);
SortedMap<K,V> headMap(K toKey);
SortedMap<K,V> tailMap(K fromKey);
}In fact, the purpose of NavigableMap is very simple and direct, which is to enhance the function of searching and obtaining elements in the collection
Treemap underlying data structure
//Sort using a comparator
private final Comparator<? super K> comparator;
//Root node of red black tree structure
private transient Entry<K,V> root;
/**
* The number of entries in the tree
* Map The number of key Val pairs in, that is, the number of node entries in the red black tree
*/
private transient int size = 0;
/**
* The number of structural modifications to the tree.
* Number of changes
*/
private transient int modCount = 0;
// Red-black mechanics
private static final boolean RED = false;
private static final boolean BLACK = true;
/**
* Node in the Tree. Doubles as a means to pass key-value pairs back to
* user (see Map.Entry).
*/
//Node of tree
static final class Entry<K,V> implements Map.Entry<K,V> {
K key;
V value;
//Left node
Entry<K,V> left;
//Right node
Entry<K,V> right;
//Parent node
Entry<K,V> parent;
//Current node attribute, black by default
boolean color = BLACK;
/**
* Make a new cell with given key, value, and parent, and with
* {@code null} child links, and BLACK color.
*/
//Construction method
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
}
The underlying storage structure of TreeMap is basically the same as that of HashMap. It is still an Entry object, storing key value pairs, references of child nodes and parent nodes, and the default node color (black);
Different from HashMap, the bottom layer of TreeMap is not an array structure. There is no array in the member variables, but is replaced by the root node. All operations are carried out through the root node.
Treemap constructor
1.Construct a new empty tree mapping,Natural sort key used
public TreeMap() {
comparator = null;
}
2.Construct a new, empty tree graph,Sort according to the given command comparator.
public TreeMap(Comparator<? super K> comparator) {
this.comparator = comparator;
}
3. Construct a new tree map, which contains the same map as the given map, and sort according to the natural sorting of its keys.
public TreeMap(Map<? extends K, ? extends V> m) {
comparator = null;
putAll(m);
}
4.A new tree contains the same mapping and map Use the same order as the specified sort map
public TreeMap(SortedMap<K, ? extends V> m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}Treemap's put
public V put(K key, V value) {
//Define root node
Entry<K,V> t = root;
//If there is no root node, initialize the root node of the red black tree
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
//Define cmp variables, which are used for comparison in binary search and value placement
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
//Define the comparator and traverse in two cases according to whether it exists or not
Comparator<? super K> cpr = comparator;
//If there is an incoming comparator (custom sorting algorithm), compare according to this rule
if (cpr != null) {
//Start from the root node and traverse down to find the determined location
do {
parent = t;
//Compare the size of the incoming key with that of the root node
cmp = cpr.compare(key, t.key);
//If the value passed in is small, it is found in the left subtree
if (cmp < 0)
t = t.left;
//If the value passed in is large, it is found in the right subtree
else if (cmp > 0)
t = t.right;
else
//If equal, the new value overrides the old value
return t.setValue(value);
} while (t != null);
//Note: there is no judgment on whether the key is null. It is suggested that you should consider it when implementing Comparator
}
else {
//There is no user-defined sorting rule for default sorting. And the key cannot be null
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
//Same way to find
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//It is explained here that there is no equal key and it is a new node
Entry<K,V> e = new Entry<>(key, value, parent);
//A new Entry can be placed under the parent, but whether it is placed on the left child node or the right child node needs to be determined according to the rules of the red black tree.
if (cmp < 0)
parent.left = e;
else
parent.right = e;
//In order to ensure the properties of red black tree, it is necessary to rotate and change color
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
1. Process initialization root node
2. According to whether there is a user-defined sorting rule, the sorting rule is traversed and searched by dichotomy.
3. Compare to determine whether it is in the left child node or the right child node. If it is the same, replace the old value and end the value setting.
4. If there is still no same key after the cycle, add an entry and place it
5. After placement, you need to consider the characteristics of the red black tree and call the fixAfterInsertion method to rotate and change color.
Treemap get
Internal call to getEntry method
public V get(Object key) {
Entry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
final Entry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
//If the comparator is not empty, call the value of the comparator's get method
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
//Start traversal down from the root node
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
//If it is less than the value of the root node, it is in the left subtree
if (cmp < 0)
p = p.left;
else if (cmp > 0)
//If it is greater than the value of the root node, it is in the right subtree
p = p.right;
else
//Equal, return the node
return p;
}
return null;
}
1. Start traversing from the root node, and gradually look down through binary search. If there is a custom comparator, call the comparator to obtain the value
2. The first cycle: start from the root node. At this time, the parent is the root node, and then compare the passed in key with the key value of the root node through k.compareTo(p.key);
3. If the key passed in is < root Key, then continue to find in the left subtree of root, starting from the left child node (root.left) of root;
If the key passed in is > root Key, then continue to find in the right subtree of root, starting from the right child node (root.right) of root;
If key = = root Key, then directly according to the value value of the root node;
The following loop rules are the same. When the traversed current node is used as the starting node, look down step by step
getEntryUsingComparator
Get value from comparator
Use the getEntry version of the comparator. Separate performance from getEntry.
(for most methods, this is not worth doing and does not depend much on comparator performance, but it is so valuable.)
final Entry<K,V> getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
//Assignment comparator
Comparator<? super K> cpr = comparator;
if (cpr != null) {
Entry<K,V> p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
}
For the action of one more assignment comparator, the principle of obtaining value is the same.
remove of Treemap
The principle of deletion is
1. Determine whether the node exists through getEntry,
2. Does not exist, return null
3. Call the deleteEntry method to delete and return the deleted value
public V remove(Object key) {
Entry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
/**
* Delete node p, and then rebalance the tree.
*/
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
//When the left and right child nodes are not null, traverse the red black tree through success (P) to find the precursor or successor
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
//Copy the predecessor or subsequent key and value to the current node P, and then delete node s (by referring to node p to s)
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/**
* At least one child node is not null. Directly replace the current node with this valued node, assign a value to the parent attribute of the replacement, and
* parent Assign values to the left attribute and right attribute of the node. At the same time, remember that the leaf node must be null, and then use the fixAfterDeletion method
* Self balancing treatment
*/
if (replacement != null) {
// Link replacement to parent
//Hang the child node of the node to be deleted to the parent node of the node to be deleted.
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
//If p is a black node, its parent and child nodes may be red. Obviously, there may be red connections. Therefore, self balancing adjustment is required
//Red does not affect
if (p.color == BLACK)
//Self balance
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
//null if there is only one node
root = null;
} else { // No children. Use self as phantom replacement and unlink.
//If the p node is black, the deletion of the p node may violate the rule that the number of black nodes on the path from each node to its leaf node is the same, so self balancing adjustment is required
if (p.color == BLACK)
fixAfterDeletion(p);
//Set the left and right nodes of the parent node to null
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
1. If the root node is deleted, set the root node to null directly;
2. The left and right child nodes of the node to be deleted are null. When deleting, set the node to null;
3. If the left and right child nodes of the node to be deleted have a value, replace the node with the node with a value;
4. If the left and right child nodes of the node to be deleted are not null, find the predecessor or successor, and copy the values of the predecessor or successor to the node,
Then delete the predecessor or successor (predecessor: the node with the largest value in the left subtree, successor: the node with the smallest value in the right subtree);
Success of Treemap
Returns the subsequent items of the specified item. If not, null is returned.
/**
* Returns the successor of the specified Entry, or null if no such.
*/
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {
//Get the right node when the right node is not empty
Entry<K,V> p = t.right;
//When the left node is not empty, the corresponding node is returned
while (p.left != null)
p = p.left;
return p;
} else {
//Get parent and child nodes
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
//When the parent node is not empty and the child node is equal to the right node of the parent node,
while (p != null && ch == p.right) {
//Assign parent node to child node
ch = p;
p = p.parent;
}
//Returns the parent node of the node
return p;
}
}
The time complexity of Treemap and why red black tree is selected
The average time complexity of searching, increasing and deleting is Olog(n)

Binary lookup tree may degenerate into linked list, so its performance is the worst. Balanced binary tree and red black tree are binary search trees with equilibrium conditions, so their efficiency is also high.
The rotation operation caused by the insertion / deletion operation of balanced binary tree may reach logn times, while the rotation operation caused by the insertion / deletion operation of red black tree is up to 2 / 3 times.
Therefore, when red and black trees appear, balanced binary trees can only appear in museums. That is, red black tree is the best choice.
LinkedHashMap
Introduction to LinkedHashMap
LinkedHashMap is a subclass of HashMap, so its bottom layer is still based on zipper hash structure. The structure consists of array and linked list + red black tree. On this basis, LinkedHashMap adds a two-way linked list to keep the same traversal order and insertion order.
2. In terms of implementation, many LinkedHashMap methods are directly inherited from HashMap (for example, the put remove method is the parent class used directly), and only some methods are overwritten to maintain the two-way linked list (the get () method is overridden). This implementation provides all optional mapping operations and does not guarantee the mapping order. In particular, it does not guarantee that the order is constant.
3 the key value pair Node used by LinkedHashMap is Entity. It inherits the Node of hashMap and adds two references, before and after. The purpose of these two references is not difficult to understand, that is, to maintain a two-way linked list
4 the process of creating a linked list starts when the key value pair node is inserted. Initially, let the head and tail references of LinkedHashMap point to the new node at the same time, and the linked list is established. Then new nodes are inserted continuously. The linked list can be updated by connecting the new node to the back of the tail reference pointing node
5. LinkedHashMap allows null values and null keys. Threads are not safe. If multiple threads access the linked hash map at the same time, and at least one thread modifies the map structurally, it must maintain external synchronization.
6 according to the order of elements in the linked list, it can be divided into: the linked list according to the insertion order and the linked list according to the access order (calling the get method).
The default is to sort by insertion order. If sorting by access order is specified, after calling the get method, the accessed elements will be moved to the end of the linked list. Continuous access can form a linked list sorted by access order. You can override the removeEldestEntry method to return a true value that specifies that the oldest element is removed when the element is inserted.
7 when traversing with Iterator, the first result is the first inserted data.
LinkedHashMap underlying structure
public class LinkedHashMap<K,V>
extends HashMap<K,V>
implements Map<K,V>
{
/*
* Implementation comments. Previous versions of this class have slightly different internal structure.
* Because the super class HashMap now uses tree nodes for some of its nodes.
* Class LinkedHashMap Entry is now regarded as an intermediate node class and can also be converted to tree form.
* The name of this class, LinkedHashMap Entry, in the current context, is confusing in several ways, but cannot be changed.
* Otherwise, even if it is not exported outside this package, some known existing source codes rely on the symbol parsing rules when calling removeEldestEntry,
* This rule suppresses compilation errors due to ambiguous usage. Therefore, we keep this name to maintain unmodified compilation.
*
* Changes in the node class also require the use of two fields (head and tail)
* Instead of pointing to the head node to maintain a double linked before/after list.
* This class has previously used different styles of callback methods in access, insert and delete.
*/
/**
* HashMap.Node Subclass of, which is applied to the node of ordinary LinkedHashMap.
*/
static class Entry<K,V> extends HashMap.Node<K,V> {
// node has key, value, hash and next
// The entry of linkedlist has been added with before and after
// TreeNode adds parent, left, right, prev and red
Entry<K,V> before, after;
Entry(int hash, K key, V value, Node<K,V> next) {
super(hash, key, value, next);
}
}
private static final long serialVersionUID = 3801124242820219131L;
/**
* The head node of the double ended queue (the oldest node)
*/
transient LinkedHashMap.Entry<K,V> head;
/**
* Tail node of double ended queue (latest node)
*/
transient LinkedHashMap.Entry<K,V> tail;
/**
* The iterative order of the hash map of this link: true for access order and false for insertion order.
* The default is false, and the insertion order is.
* @serial
*/
final boolean accessOrder;LinkedHashMap constructor
/**
* Constructs an empty LinkedHashMap instance in insertion order using the specified initial capacity and load factor.
*
* @param initialCapacity the initial capacity
* @param loadFactor the load factor
* @throws IllegalArgumentException if the initial capacity is negative
* or the load factor is nonpositive
*/
public LinkedHashMap(int initialCapacity, float loadFactor) {
// Method to call hashmap
super(initialCapacity, loadFactor);
// The default is false, and the insertion order is
accessOrder = false;
}
/**
* C Construct an empty LinkedHashMap instance in insertion order using the specified initial capacity and the default load factor (0.75).
*
* @param initialCapacity the initial capacity
* @throws IllegalArgumentException if the initial capacity is negative
*/
public LinkedHashMap(int initialCapacity) {
super(initialCapacity);
accessOrder = false;
}
/**
* Construct an empty LinkedHashMap instance in insertion order using the default initial capacity (16) and load factor (0.75).
*/
public LinkedHashMap() {
super();
accessOrder = false;
}
/**
* Construct LinkedHashMap instances in insertion order using the same mapping as the specified mapping.
* LinkedHashMap The instance is created using the default load factor (0.75) and an initial capacity sufficient to accommodate the specified mapping.
*
* @param m the map whose mappings are to be placed in this map
* @throws NullPointerException if the specified map is null
*/
public LinkedHashMap(Map<? extends K, ? extends V> m) {
super();
accessOrder = false;
putMapEntries(m, false);
}
/**
* Construct an empty LinkedHashMap instance with the specified initial capacity, load factor, and sort pattern.
*
* @param initialCapacity the initial capacity
* @param loadFactor the load factor
* @param accessOrder the ordering mode - <tt>true</tt> for
* access-order, <tt>false</tt> for insertion-order
* @throws IllegalArgumentException if the initial capacity is negative
* or the load factor is nonpositive
*/
public LinkedHashMap(int initialCapacity,
float loadFactor,
boolean accessOrder) {
super(initialCapacity, loadFactor);
this.accessOrder = accessOrder;
}How does LinkedHashMap maintain order
put,newNode,afterNodeAccess,afterInsertion
Other methods invoked in the put method of HashMap have been rewritten in LinkedHashMap.
/**
* Implements Map.put and related methods
*
* @param hash hash for key
* @param key the key
* @param value the value to put
* @param onlyIfAbsent if true, don't change existing value
* @param evict if false, the table is in creation mode.
* @return previous value, or null if none
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
/**
* If the table array of the current HashMap has not been defined or its length has not been initialized, first expand it through resize(),
* Returns the length of the expanded array n
*/
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
//The corresponding array subscript is obtained by bitwise AND & operation through the array length and hash value. If there is no element at this position, the new Node directly inserts the new element
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
//Otherwise, there are already elements in this position, and we need to do some other operations
else {
Node<K,V> e; K k;
//If the inserted key is the same as the original key, you can replace it
if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
e = p;
/**
* Otherwise, if the key is different, judge whether the current Node is a TreeNode. If so, execute putTreeVal to insert a new element
* Go to the red and black tree.
*/
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
//If it is not a TreeNode, perform linked list traversal
else {
for (int binCount = 0; ; ++binCount) {
/**
* If the same element is not found after the last node in the linked list, perform the following operations and insert it directly into the new Node,
* But conditional judgment may be transformed into red black tree
*/
if ((e = p.next) == null) {
//Directly new a Node
p.next = newNode(hash, key, value, null);
/**
* TREEIFY_THRESHOLD=8,Because binCount starts from 0, that is, when the length of the linked list exceeds 8 (inclusive),
* Turn into red and black trees.
*/
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
/**
* If the same key value is found before the last node of the linked list (which does not conflict with the above judgment, it is directly through the array)
* If the subscript determines whether the key value is the same, replace it
*/
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
//When onlyIfAbsent is true: when an element already exists at a certain location, it will not be overwritten
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
//Finally, judge the critical value and whether to expand the capacity.
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}newNode method
First, LinkedHashMap rewrites the newNode() method, which ensures the insertion order.
/**
* Use the internal class Entry in LinkedHashMap
*/
Node<K,V> newNode(int hash, K key, V value, Node<K,V> e) {
LinkedHashMap.Entry<K,V> p = new LinkedHashMap.Entry<K,V>(hash, key, value, e);
linkNodeLast(p);
return p;
}
/**
* Take the newly created node p as the tail node,
* Of course, if the first node is stored, it is both a head node and a tail node. At this time, both before and after of node p are null
* Otherwise, establish a linked list relationship with the last tail node, and set the previous node of the current tail node p as the last tail node,
* Set the last node (after) of the last tail node as the current tail node p
* Through this method, the bidirectional linked list function is realized, and the values of before, after, head and tail are set
*/
private void linkNodeLast(LinkedHashMap.Entry<K,V> p) {
LinkedHashMap.Entry<K,V> last = tail;
tail = p;
if (last == null)
head = p;
else {
p.before = last;
last.after = p;
}
}afterNodeAccess method
Secondly, the afterNodeAccess() method is not specifically implemented in HashMap, but rewritten in LinkedHashMap. The purpose is to ensure that the operated Node is always last, so as to ensure the reading order. It will be used when calling the put method and get method.
/**
* When accessOrder is true and the incoming node is not the last, move the incoming node to the last
*/
void afterNodeAccess(Node<K,V> e) {
//Last tail node before method execution
LinkedHashMap.Entry<K,V> last;
//When accessOrder is true and the incoming node is not the last tail node, execute the following method
if (accessOrder && (last = tail) != e) {
LinkedHashMap.Entry<K,V> p =
(LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
//p: Current node
//b: The previous node of the current node
//a: The next node of the current node;
//Setting p.after to null breaks the relationship with the latter node, but its location has not been determined
p.after = null;
/**
* Because the current node p is removed, node b and node a are disconnected. We first establish a connection with node a from the perspective of node b
* If node b is null, it means that the current node p is the head node. After node p is removed, the next node a of p is the head node;
* Otherwise, the next node of node b is set as node a
*/
if (b == null)
head = a;
else
b.after = a;
/**
* Because the current node p is removed, node A and node b are disconnected. We establish a connection with node b from the perspective of node a
* If node a is null, it means that the current node p is the tail node. After node p is removed, the previous node b of p is the tail node,
* However, instead of directly assigning node p to tail, we give a local variable last (i.e. the last current node), because
* The direct assignment to tail is not consistent with the final goal of this method; If node a is not null, set the previous node of node a to node b
*
* (Because it has been judged (last = tail)= e. This indicates that the incoming node is not a tail node. Since it is not a tail node, then
* e.after It must not be null, so why is a == null judged here?
* In my understanding, java can destroy the encapsulation through reflection mechanism, so if all Entry entities are created by reflection, they may not meet the above requirements
* (judgment conditions)
*/
if (a != null)
a.before = b;
else
last = b;
/**
* Under normal circumstances, last should not be empty. Why should we judge? The reason is the same as before
* Previously set p.after to null. Here, set its before value to the last tail node, and set the last tail node at the same time
* last Set to this p
*/
if (last == null)
head = p;
else {
p.before = last;
last.after = p;
}
//Finally, node p is set as the tail node, and it's done
tail = p;
++modCount;
}
}When accessOrder is false, your access order is the order you first inserted; When accessOrder is true, any operation, including put and get, will change the existing storage order in the map.
afterNodeInsertion method
We can see that the afterNodeInsertion(boolean evict) method is also rewritten in the LinkedHashMap. Its purpose is to remove the oldest node object in the linked list, that is, the node object currently in the head, but it will not be executed in JDK8 because the removeEldestEntry method always returns false. Look at the source code:
void afterNodeInsertion(boolean evict) { // possibly remove eldest
LinkedHashMap.Entry<K,V> first;
if (evict && (first = head) != null && removeEldestEntry(first)) {
K key = first.key;
removeNode(hash(key), key, null, false, true);
}
}
protected boolean removeEldestEntry(Map.Entry<K,V> eldest) {
return false;
}get,remove
The difference between the get method of LinkedHashMap and the get method of HashMap lies in the addition of afterNodeAccess() method
public V get(Object key) {
Node<K,V> e;
if ((e = getNode(hash(key), key)) == null)
return null;
if (accessOrder)
afterNodeAccess(e);
return e.value;
}The remove method also directly uses the remove in the HashMap, which is not explained in the HashMap chapter, because the principle of remove is very simple. Calculate the hash through the passed parameter key, and then you can find the corresponding node node.next, if the node node is a node directly in the array, set the element at this position of the table array to node next; If it is in the linked list, traverse the linked list until the corresponding node node is found, and then establish the next of the previous node of the node as the next of the node.
LinkedHashMap rewrites afterNodeRemoval(Node e). This method is not specifically implemented in HashMap. This method adjusts the structure of the double linked list when deleting nodes.
The deletion process is not complicated. In fact, three things are done:
Locate the bucket position according to the hash
Traverse the linked list or call the red black tree related deletion method
Remove the node to be deleted from the double linked list maintained by LinkedHashMap
void afterNodeRemoval(Node<K,V> e) {
LinkedHashMap.Entry<K,V> p = (LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
//Set before and after of the node to be deleted to null
p.before = p.after = null;
/**
* If node b is null, it means that node p to be deleted is the head node. After the node is removed, the next node a of the node is the head node
* Otherwise, set the after attribute of the previous node b of the node to be deleted to node a
*/
if (b == null)
head = a;
else
b.after = a;
/**
* If node a is null, it means that node p to be deleted is the tail node. After the node is removed, the previous node a of the node is the tail node
* Otherwise, set the before attribute of the next node a of the node to be deleted to node b
*/
if (a == null)
tail = b;
else
a.before = b;
}LinkedHashMap implements LRU
LRU # is the abbreviation of Least Recently Used
Override the removeEldestEntry method to implement your elimination strategy.
In the put method, the afterNodeInsertion method is invoked and the removeEldestEntry method is invoked. If removeNode is returned, the removeNode(first.key) method is called.
public class LRUCache<K, V> extends LinkedHashMap<K, V> {
private static final long serialVersionUID = 1L;
private final int maxSize;
public LRUCache(int maxSize){
this(maxSize, 16, 0.75f, false);
}
public LRUCache(int maxSize, int initialCapacity, float loadFactor, boolean accessOrder){
super(initialCapacity, loadFactor, accessOrder);
this.maxSize = maxSize;
}
protected boolean removeEldestEntry(Map.Entry<K, V> eldest) {
return this.size() > this.maxSize;
}
}