This article is excerpted from "design patterns should be learned this way"
1 parsing mathematical expressions using interpreter patterns
The following uses the interpreter mode to implement a mathematical expression calculator, including addition, subtraction, multiplication and division.
First, define the abstract expression role IArithmeticInterpreter interface.
public interface IArithmeticInterpreter {
int interpret();
}Create the Interpreter abstract class for the terminating expression role.
public abstract class Interpreter implements IArithmeticInterpreter {
protected IArithmeticInterpreter left;
protected IArithmeticInterpreter right;
public Interpreter(IArithmeticInterpreter left, IArithmeticInterpreter right) {
this.left = left;
this.right = right;
}
}Then create non terminator expression role addition, subtraction, multiplication and division interpreters respectively. The code of addition expression AddInterpreter class is as follows.
public class AddInterpreter extends Interpreter {
public AddInterpreter(IArithmeticInterpreter left, IArithmeticInterpreter right) {
super(left, right);
}
public int interpret() {
return this.left.interpret() + this.right.interpret();
}
}The code of the SubInterpreter class of the subtraction expression is as follows.
public class SubInterpreter extends Interpreter {
public SubInterpreter(IArithmeticInterpreter left, IArithmeticInterpreter right) {
super(left, right);
}
public int interpret() {
return this.left.interpret() - this.right.interpret();
}
}The code of multiplication expression MultiInterpreter class is as follows.
public class MultiInterpreter extends Interpreter {
public MultiInterpreter(IArithmeticInterpreter left, IArithmeticInterpreter right){
super(left,right);
}
public int interpret() {
return this.left.interpret() * this.right.interpret();
}
}The code of DivInterpreter class of division expression is as follows.
public class DivInterpreter extends Interpreter {
public DivInterpreter(IArithmeticInterpreter left, IArithmeticInterpreter right){
super(left,right);
}
public int interpret() {
return this.left.interpret() / this.right.interpret();
}
}The code of NumInterpreter class of numeric expression is as follows.
public class NumInterpreter implements IArithmeticInterpreter {
private int value;
public NumInterpreter(int value) {
this.value = value;
}
public int interpret() {
return this.value;
}
}Next, create the calculator GPCalculator class.
public class GPCalculator {
private Stack<IArithmeticInterpreter> stack = new Stack<IArithmeticInterpreter>();
public GPCalculator(String expression) {
this.parse(expression);
}
private void parse(String expression) {
String [] elements = expression.split(" ");
IArithmeticInterpreter left,right;
for (int i = 0; i < elements.length ; i++) {
String operator = elements[i];
if(OperatorUtil.ifOperator(operator)){
left = this.stack.pop();
right = new NumInterpreter(Integer.valueOf(elements[++i]));
System.out.println("Out of stack" + left.interpret() + "and" + right.interpret());
this.stack.push(OperatorUtil.getInterpreter(left,right,operator));
System.out.println("Apply operator:" + operator);
}else {
NumInterpreter numInterpreter = new NumInterpreter(Integer.valueOf(elements[i]));
this.stack.push(numInterpreter);
System.out.println("Stack:" + numInterpreter.interpret());
}
}
}
public int calculate() {
return this.stack.pop().interpret();
}
}The code of the tool class OperatorUtil is as follows.
public class OperatorUtil {
public static boolean isOperator(String symbol) {
return (symbol.equals("+") || symbol.equals("-") || symbol.equals("*"));
}
public static Interpreter getInterpreter(IArithmeticInterpreter left, IArithmeticInterpreter
right, String symbol) {
if (symbol.equals("+")) {
return new AddInterpreter(left, right);
} else if (symbol.equals("-")) {
return new SubInterpreter(left, right);
} else if (symbol.equals("*")) {
return new MultiInterpreter(left, right);
} else if (symbol.equals("/")) {
return new DivInterpreter(left, right);
}
return null;
}
}Finally, write the client test code.
public static void main(String[] args) {
System.out.println("result: " + new GPCalculator("10 + 30").calculate());
System.out.println("result: " + new GPCalculator("10 + 30 - 20").calculate());
System.out.println("result: " + new GPCalculator("100 * 2 + 400 * 1 + 66").calculate());
}The operation results are shown in the figure below.
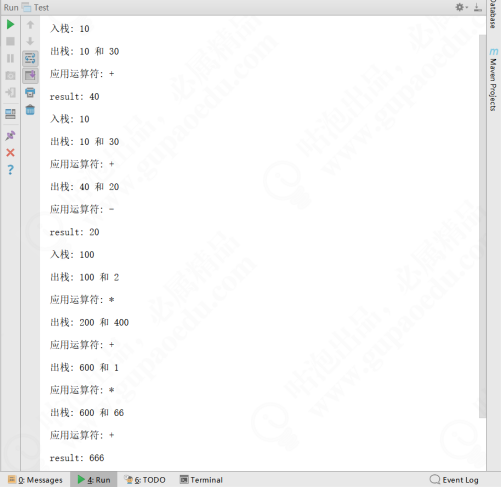
Of course, the above simple calculator does not consider priority, which operates from left to right. In practical operations, multiplication and division belong to primary operations, and addition and subtraction belong to secondary operations. First level operation requires priority calculation. In addition, we can manually adjust the priority of operations by using parentheses. Let's optimize the code again. First, create an enumeration class.
public enum OperatorEnum {
LEFT_BRACKET("("),
RIGHT_BRACKET(")"),
SUB("-"),
ADD("+"),
MULTI("*"),
DIV("/"),
;
private String operator;
public String getOperator() {
return operator;
}
OperatorEnum(String operator) {
this.operator = operator;
}
}Then modify the processing logic of OperatorUtil and set two stacks.
public class OperatorUtil {
public static Interpreter getInterpreter(Stack<IArithmeticInterpreter> numStack, Stack<String> operatorStack) {
IArithmeticInterpreter right = numStack.pop();
IArithmeticInterpreter left = numStack.pop();
String symbol = operatorStack.pop();
System.out.println("Digital out of stack:" + right.interpret() + "," + left.interpret() + ",Operator out of stack:" + symbol);
if (symbol.equals("+")) {
return new AddInterpreter(left, right);
} else if (symbol.equals("-")) {
return new SubInterpreter(left, right);
} else if (symbol.equals("*")) {
return new MultiInterpreter(left, right);
} else if (symbol.equals("/")) {
return new DivInterpreter(left, right);
}
return null;
}
}Modify the code of GPCalculator.
public class GPCalculator {
//Digital stack
private Stack<IArithmeticInterpreter> numStack = new Stack<IArithmeticInterpreter>();
//Operator stack
private Stack<String> operatorStack = new Stack<String>();
/**
* Analytical expression
* @param expression
*/
public GPCalculator(String expression) {
this.parse(expression);
}
private void parse(String input) {
//Remove empty characters from expressions
String expression = this.fromat(input);
System.out.println("Standard expression:" + expression);
for (String s : expression.split(" ")) {
if (s.length() == 0){
//If it is a space, continue the loop and do nothing
continue;
}
//If it is addition and subtraction, because the priority of addition and subtraction is the lowest, as long as the addition and subtraction sign is encountered here, no matter what operator is in the operator stack, it must be operated
else if (s.equals(OperatorEnum.ADD.getOperator())
|| s.equals(OperatorEnum.SUB.getOperator())) {
//When the stack is not empty, and the top element in the stack is any one of addition, subtraction, multiplication and division
while (!operatorStack.isEmpty()
&&(operatorStack.peek().equals(OperatorEnum.SUB.getOperator())
|| operatorStack.peek().equals(OperatorEnum.ADD.getOperator())
|| operatorStack.peek().equals(OperatorEnum.MULTI.getOperator())
|| operatorStack.peek().equals(OperatorEnum.DIV.getOperator()))) {
//The results are stored in the stack
numStack.push(OperatorUtil.getInterpreter(numStack,operatorStack));
}
//After the operation, put the current operator on the stack
System.out.println("Operator stack:"+s);
operatorStack.push(s);
}
//When the current operator is multiplication and division, it takes precedence over addition and subtraction
//Therefore, it is necessary to judge whether the uppermost is multiplication and division. If it is multiplication and division, it will be calculated. Otherwise, it will be directly put on the stack
else if (s.equals(OperatorEnum.MULTI.getOperator())
|| s.equals(OperatorEnum.DIV.getOperator())) {
while (!operatorStack.isEmpty()&&(
operatorStack.peek().equals(OperatorEnum.MULTI.getOperator())
|| operatorStack.peek().equals(OperatorEnum.DIV.getOperator()))) {
numStack.push(OperatorUtil.getInterpreter(numStack,operatorStack));
}
//Stack the current operator
System.out.println("Operator stack:"+s);
operatorStack.push(s);
}
//If it is an open bracket, it will be directly put on the stack without any operation. The trim() function is used to remove spaces. Due to the above segmentation operation, the operator may contain spaces
else if (s.equals(OperatorEnum.LEFT_BRACKET.getOperator())) {
System.out.println("Operator stack:"+s);
operatorStack.push(OperatorEnum.LEFT_BRACKET.getOperator());
}
//If it is a right parenthesis, the operator in the stack is cleared to the left parenthesis
else if (s.equals(OperatorEnum.RIGHT_BRACKET.getOperator())) {
while (!OperatorEnum.LEFT_BRACKET.getOperator().equals(operatorStack.peek())) {
//Start operation
numStack.push(OperatorUtil.getInterpreter(numStack,operatorStack));
}
//Clear the left parenthesis after the operation
String pop = operatorStack.pop();
System.out.println("After the bracket operation is completed, clear the right bracket in the stack:"+pop);
}
//If it is a number, it is directly put into the stack of data
else {
//Convert a numeric string into a number and store it on the stack
NumInterpreter numInterpreter = new NumInterpreter(Integer.valueOf(s));
System.out.println("Digital stack:"+s);
numStack.push(numInterpreter);
}
}
//Finally, when the stack is not empty, continue the operation until the stack is empty
while (!operatorStack.isEmpty()) {
numStack.push(OperatorUtil.getInterpreter(numStack,operatorStack));
}
}
/**
* Calculation result out of stack
* @return
*/
public int calculate() {
return this.numStack.pop().interpret();
}
/**
* Change to standard form to facilitate segmentation
* @param expression
* @return
*/
private String fromat(String expression) {
String result = "";
for (int i = 0; i < expression.length(); i++) {
if (expression.charAt(i) == '(' || expression.charAt(i) == ')' ||
expression.charAt(i) == '+' || expression.charAt(i) == '-' ||
expression.charAt(i) == '*' || expression.charAt(i) == '/')
//Add a space between the operator and the number
result += (" " + expression.charAt(i) + " ");
else
result += expression.charAt(i);
}
return result;
}
}At this point, let's look at the client test code.
public static void main(String[] args) {
System.out.println("result: " + new GPCalculator("10+30/((6-4)*2-2)").calculate());
}Run to get the expected results, as shown in the figure below.
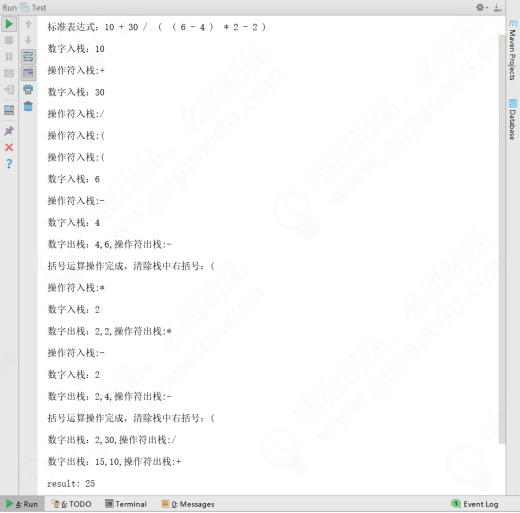
2 Application of Interpreter pattern in JDK source code
Let's first look at the compilation and parsing of regular expressions by Pattern in the JDK source code.
public final class Pattern implements java.io.Serializable {
...
private Pattern(String p, int f) {
pattern = p;
flags = f;
if ((flags & UNICODE_CHARACTER_CLASS) != 0)
flags |= UNICODE_CASE;
capturingGroupCount = 1;
localCount = 0;
if (pattern.length() > 0) {
compile();
} else {
root = new Start(lastAccept);
matchRoot = lastAccept;
}
}
...
public static Pattern compile(String regex) {
return new Pattern(regex, 0);
}
public static Pattern compile(String regex, int flags) {
return new Pattern(regex, flags);
}
...
}Application of Interpreter pattern in Spring source code
Let's look at the ExpressionParser interface in Spring.
public interface ExpressionParser {
Expression parseExpression(String expressionString) throws ParseException;
Expression parseExpression(String expressionString, ParserContext context) throws ParseException;
}Here we do not explain the source code in depth. We can roughly understand its principle through the cases we wrote earlier. You might as well write a piece of client code to verify it. The client test code is as follows.
public static void main(String[] args) {
ExpressionParser parser = new SpelExpressionParser();
Expression expression = parser.parseExpression("100 * 2 + 400 * 1 + 66");
int result = (Integer) expression.getValue();
System.out.println("The calculation result is:" + result);
}
The operation results are shown in the figure below.
It can be seen from the above figure that the operation results are consistent with the expected results.