Focus on official account: high performance architecture exploration. The background replies to [data], which can be collected free of charge

 

As the saying goes: learning is like sailing against the current. If you don't advance, you will retreat; The heart is like a horse on the plain, easy to put but difficult to collect. This sentence is deeper for programmers. The business is getting more and more rolling. I'm always ready, 😃. Binary tree, in the interview, has been a necessary appetizer. In the binary tree related interview questions, traversal is a common test question. This paper will analyze and explain the traversal of binary tree from the perspective of recursion and non recursion.

ergodic

Traversal of binary tree refers to starting from the root node and accessing all nodes in the binary tree in a certain order, so that each node is accessed and only once.

The traversal of binary tree includes pre order traversal, middle order traversal and subsequent traversal.

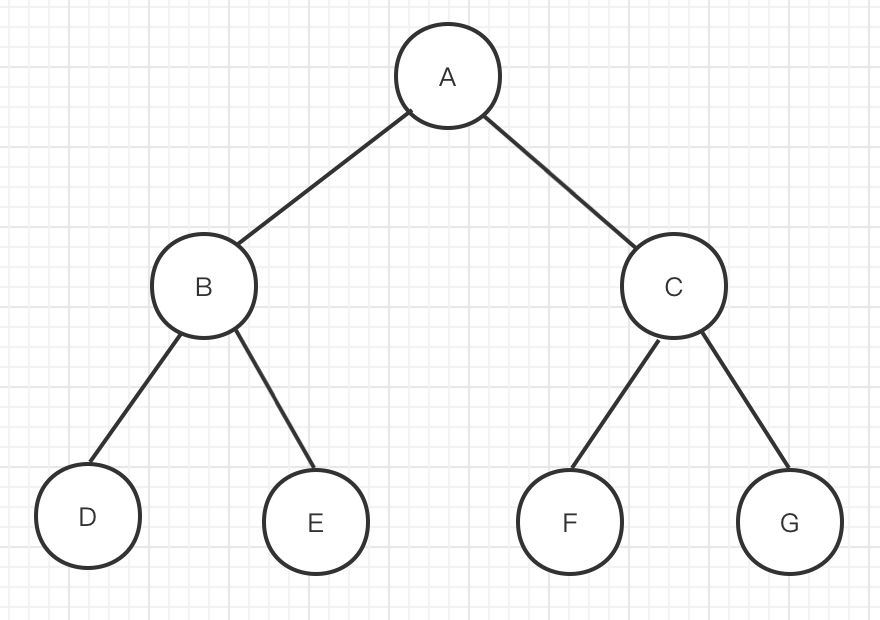
Figure I

Among the above three traversal methods, the first order, middle order and last order are the parent node relative to the child node. If the parent node precedes the child node, it is a preorder traversal. If the child node precedes the parent node, it is a postorder traversal. For child nodes, if the left node is first, then the parent node, and then the right node, then it is medium order traversal.

As shown in Figure 1, the three traversal results of binary tree are as follows:

Preorder traversal: a - > b - > D - > e - > C - > F - > G

Middle order traversal: D - > b - > e - > A - > F - > C - > G

Subsequent traversal: D - > e - > b - > F - > G - > C - > A

In order to understand the code, we first define the node definition of the tree:

struct TreeNode {
  TreeNode *left;
  TreeNode *right;
  int val;
};

Preorder traversal

Definition: first access the parent node, then traverse the left subtree, and finally traverse the right subtree.

recursion

I believe that recursive traversal will be easy for everyone to write, and bugfree. Because the implementation code is very simple.

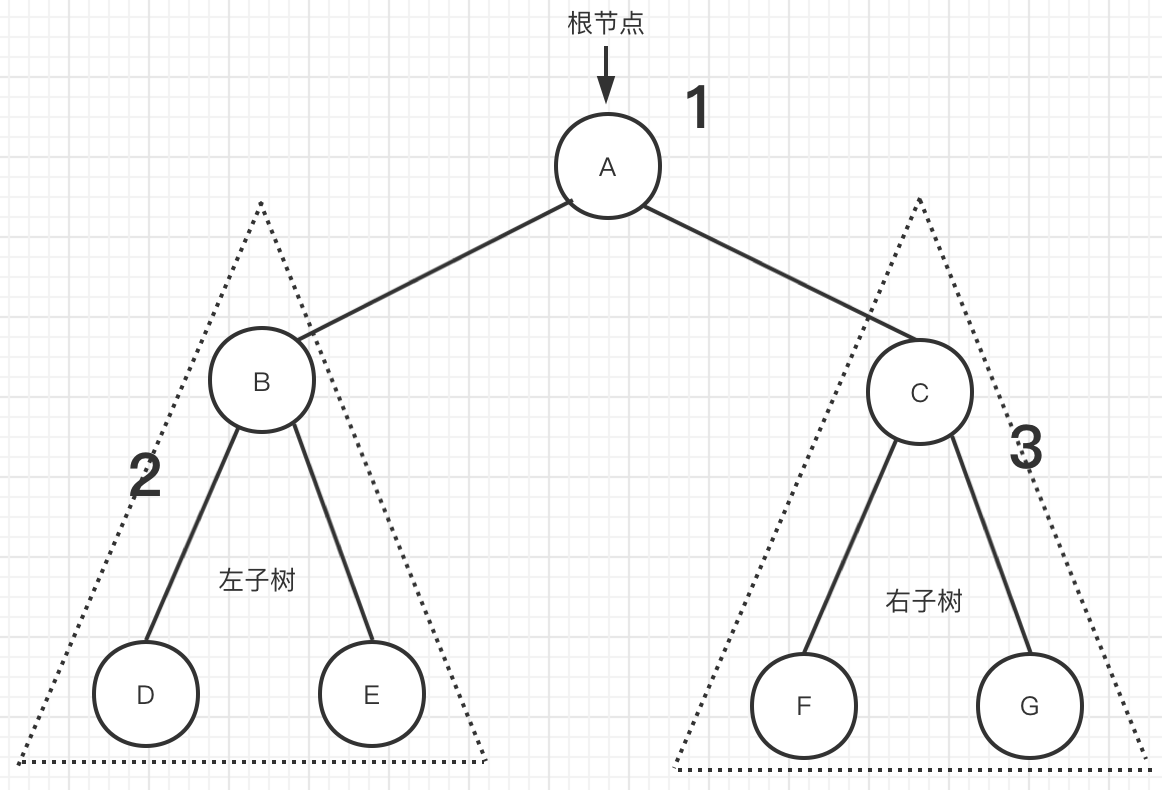
Figure 2 preorder traversal

In the above figure [figure 2], recursive traversal is used, that is, the left subtree and right subtree are treated as one tree. The code is as follows:

void PreOrder(TreeNode *root) {
   if (!root) {
     return;
   }
   
   //Traverse the root node (here is only output, and readers can also process it according to actual needs, such as storage)
   std::cout << root->val << std::endl;
   
   //Traverse left subtree
   PreOrder(root->left);
   
   //Traversing right subtree
   PreOrder(root->right);
}

non-recursive

In the non recursive operation, we still visit the root node first, then traverse the left subtree, and then traverse the right subtree.

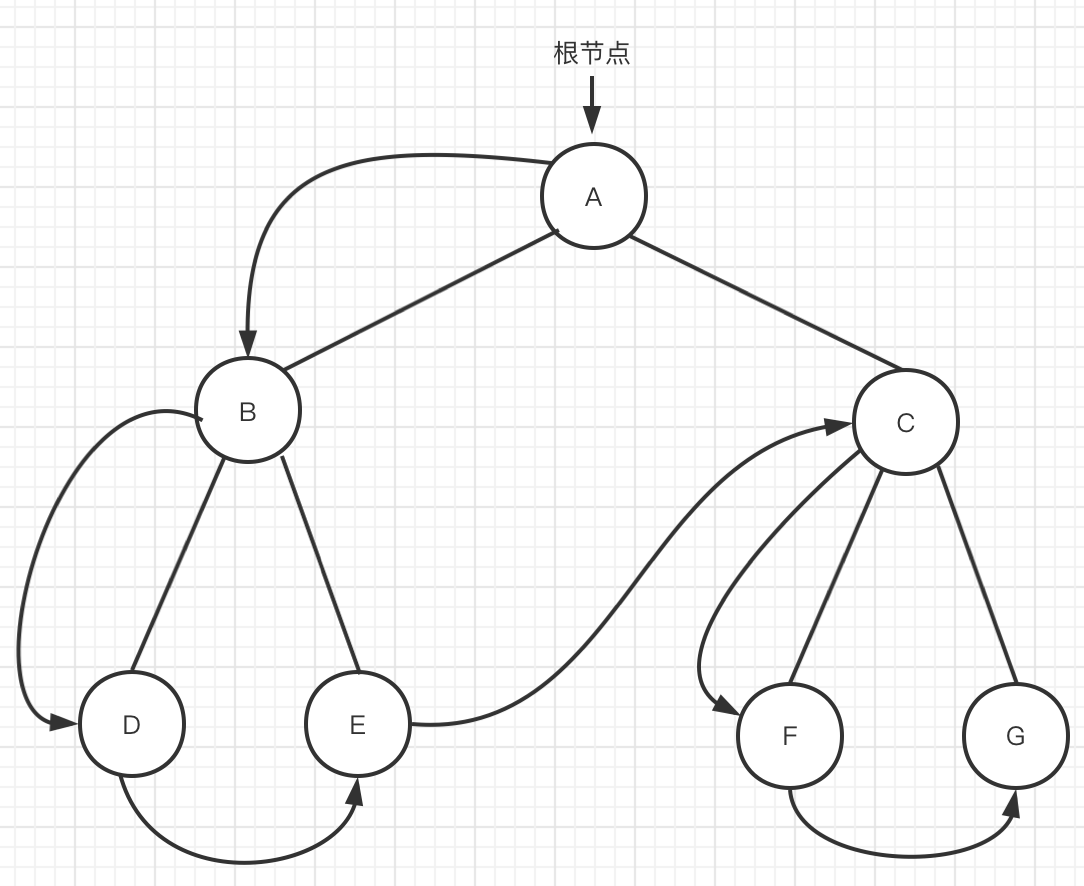
Figure 3 preorder traversal

1. Reach node a, access node a, and start traversing the left subtree of A

2. Reach node B, access node B, and start traversing the left subtree of B

3. Reach node D and access node D. because node D has no subtree, node D traversal is completed

   • Node D traversal is completed, which means that the left subtree of node B is traversed, so it then traverses the right subtree of node B

4. Reach node E and access node E. Because node E has no subtree, node e traversal is complete

   • The completion of node E traversal means that the right subtree traversal of node B is completed, which also indicates that the subtree traversal of node B is completed

   • Start traversing the right subtree of node A

5. Arrive at node C and access node C. Start traversing the left subtree of C

6. Arrive at node F and access node F. Because node f has no subtree, node f traversal is complete

   • The traversal of node F is completed, which means that the traversal of the left subtree of node C is completed, so start traversing the right subtree of node C

7. To node g, access node G. Because node G has no subtree, node g traversal is completed

   • The completion of node G traversal means that the right subtree traversal of node C is completed, which indicates that node C traversal is completed

   • The completion of node C traversal means that the right subtree traversal of node A is completed, which in turn means that node A traversal is completed. Therefore, the tree traversal with A as the root node is completed.

To traverse a binary tree in a non recursive way, you need to introduce an additional data structure stack. The basic process is as follows: 1. Apply for a stack stack, and then press the head node into the stack.

2. Pop up the stack top node from the stack and print

3. Press its right child node (if it is not empty) into the stack first

4. Press its left child node (if not empty) into the stack.

5. Repeat steps 2, 3 and 4 until the stack is empty and the whole process is over.

The code is as follows:

void PreOrder(TreeNode *root) {
  if (!root) {
    return;
  }
  
  std::stack<TreeNode*> s;
  s.push(root); //Step 1
  
  while (!s.empty()) {
    auto t = s.top();
    s.pop();//Out of stack
    
    std::cout << t->val << std::endl; //Access node
    if (t->right) {
      s.push(t->right); //Corresponding to step 3
    }
    
    if (t->left) {
      s.push(t->left); //Corresponding to step 4
    }
  }
}

Medium order traversal

Definition: first traverse the left subtree, access the root node, and traverse the right subtree

recursion

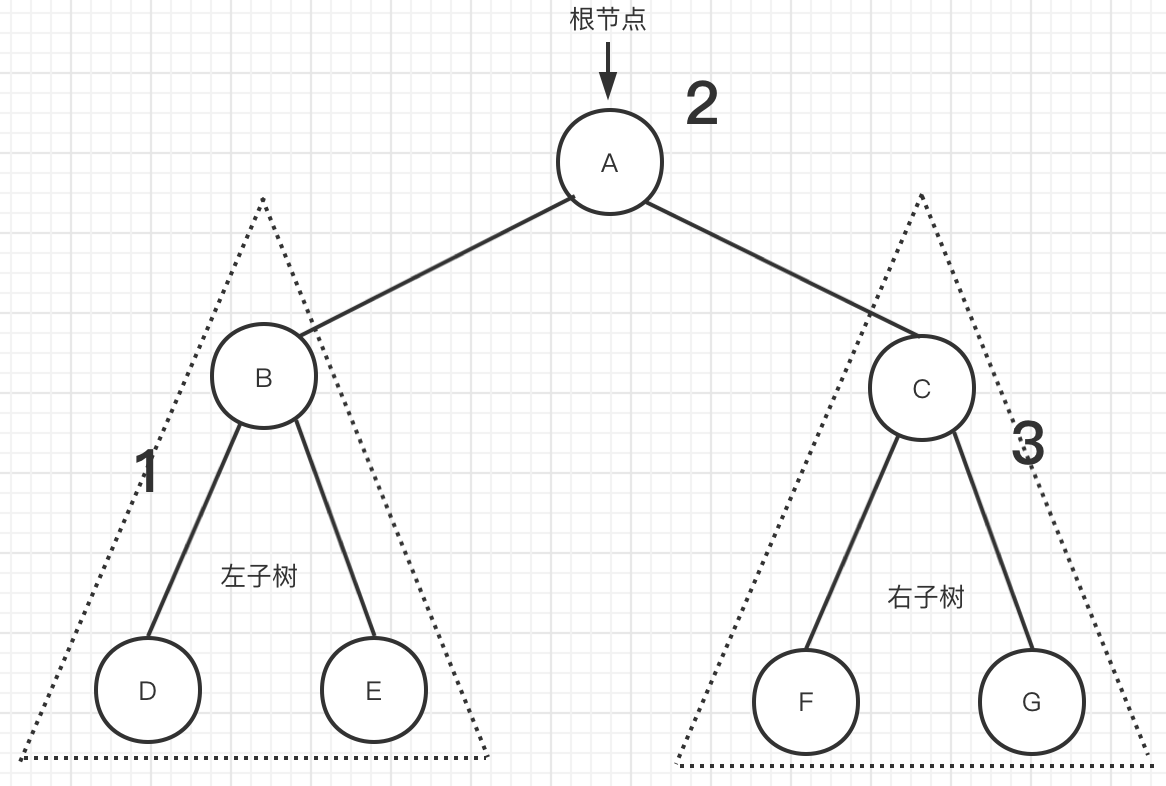
Sequence traversal in Figure 4

In the above figure [figure 4], recursive traversal is used, that is, the left subtree and right subtree are treated as one tree. The code is as follows:

void InOrder(TreeNode *root) {
   if (!root) {
     return;
   }
   
  
   
   //Traverse left subtree
   InOrder(root->left);
   
    //Traverse the root node (here is only output, and readers can also process it according to actual needs, such as storage)
   std::cout << root->val << std::endl;
   
   //Traversing right subtree
   InOrder(root->right);
}

The recursive code of the above middle order traversal, compared with the first order traversal, only places the behavior of accessing the root node between the left and right subtrees.

non-recursive

In the non recursive operation, we still traverse the left subtree, then access the root node, and finally traverse the right subtree.

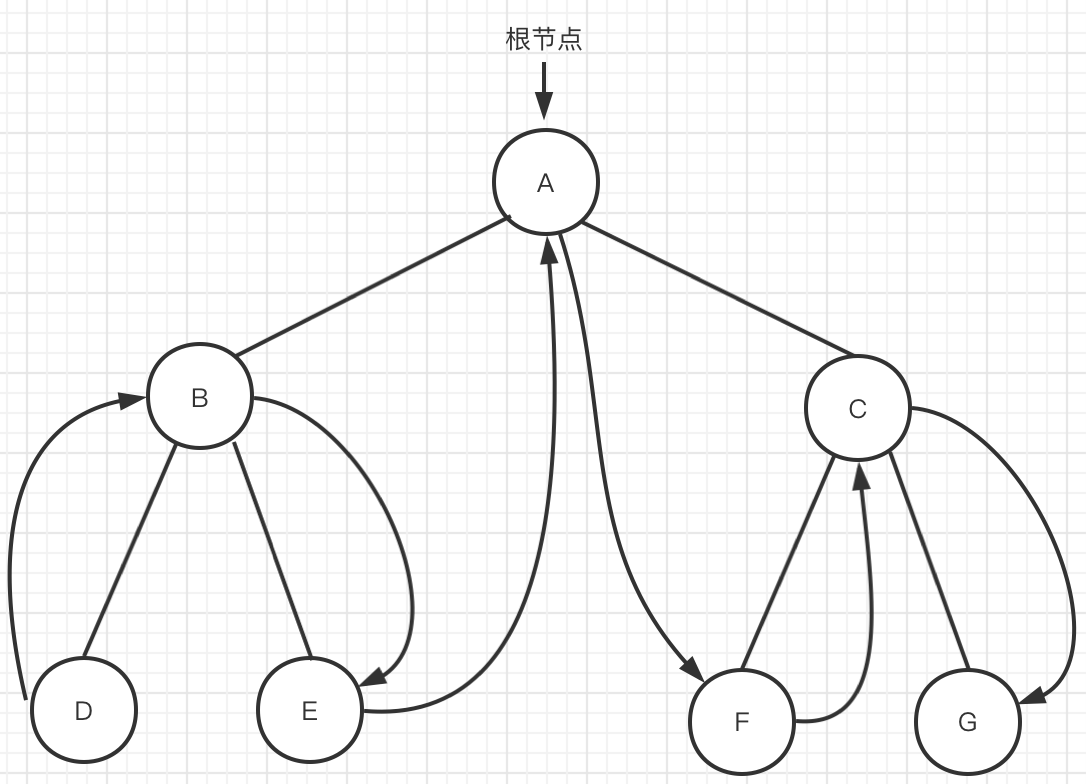
Sequence traversal in Figure 5

1. Reach node A, node A has A left subtree, and traverse the left subtree of node A

2. Arrive at node B, node B has a left subtree, and traverse the left subtree of node B

3. When node D is reached, node D has no subtree. Access node D

   • Since D has no subtree, it means that the traversal of the left subtree of B is completed, so it returns to node B

4. Access node B and traverse the right subtree of node B

5. Reach node e, node E has no subtree, and access node E

   • The traversal of node E is completed, which means that the traversal of the subtree with B as the root is completed and returns to node A

6. Reach node A, access node A, and traverse the right subtree of node A

7. Reach node C and traverse the left subtree of node C

8. Arrive at node F, because node f has no subtree, so visit node F.

   • Since node F has no subtree, it means that the traversal of the left subtree of node C is completed and returns to node C

9. Reach node C, access node C, and traverse the right subtree of C

10. Node G is reached because G has no subtree because node G is accessed

• The traversal of node G means that the traversal of the right subtree of node C is completed, which in turn means that the traversal of the right subtree of node A is completed, which means that the traversal of the binary tree with node A as the root is completed.

Medium order traversal also requires additional auxiliary data structure stacks.

1. Put the root node on the stack 2. If the root node has a left subtree, put the root node of the left subtree on the stack 3. Repeat steps 1 and 2 Continue to traverse the left subtree 4. Pop up the node from the stack for access, and then traverse the right subtree (repeat steps 1 and 2) 5. If the stack is empty, the traversal is completed

The code is as follows:

void InOrder(TreeNode *root) {
  if (!root) {
    return;
  }
  
  std::stack<TreeNode*> s;
  auto p = root;
  
  while (!s.empty() || p) {
    if (p) { //Steps 1 and 2
      s.push(p);
      p = p->left;
    } else { //Step 4
      auto t = s.top();
      std::cout << t->val << std::endl;
      p = t->right;
    }
  }
}

Subsequent traversal

Definition: first traverse the left subtree, then traverse the right subtree, and finally access the root node

recursion

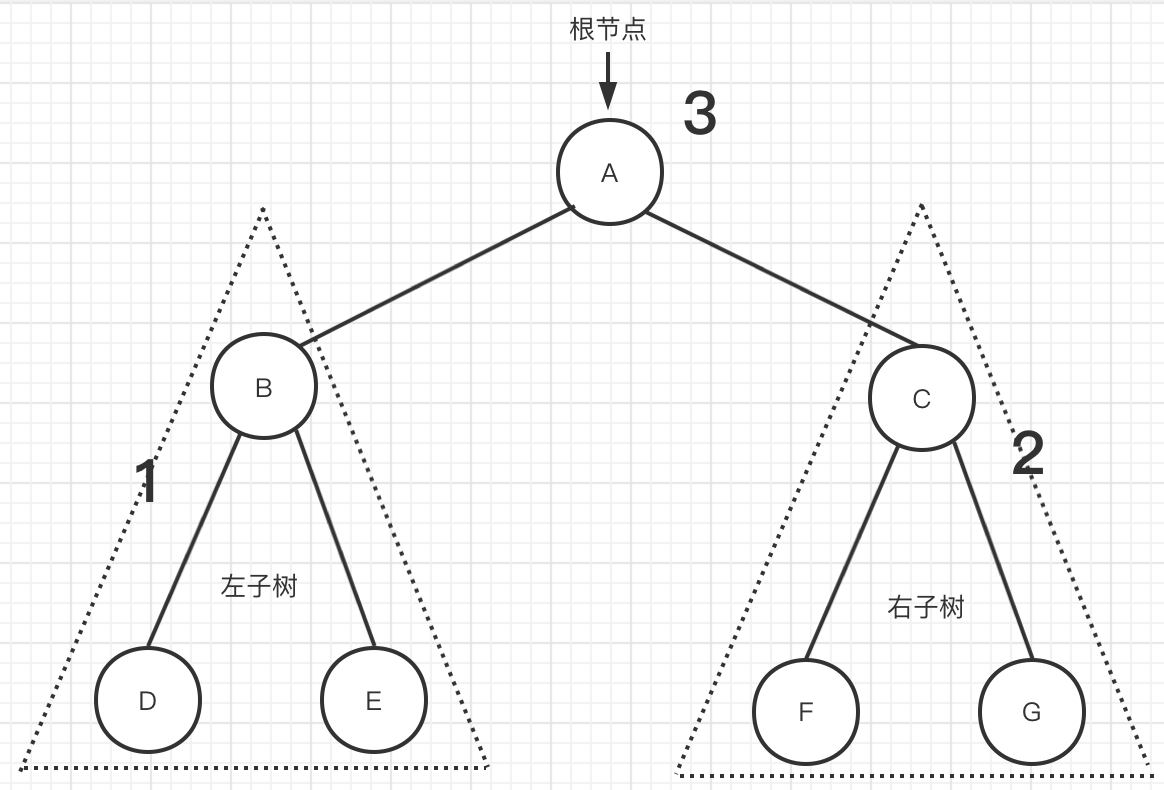
Figure 6 post order traversal

void PostOrder(TreeNode *root) {
   if (!root) {
     return;
   }
   
   //Traverse left subtree
   PostOrder(root->left);
   
   //Traversing right subtree
   PostOrder(root->right);
   
    //Traverse the root node (here is only output, and readers can also process it according to actual needs, such as storage)
   std::cout << root->val << std::endl;
}

The above is the recursive writing method of subsequent traversal. Comparing the recursive writing methods of writing preorder traversal, middle order traversal and subsequent traversal, most of the codes are the same, and the only difference is that the code positions of accessing the root node are different:

First order traversal: first access the root node, then traverse the left subtree, and finally traverse the right subtree. Second order traversal: first traverse the left subtree, then access the root node, and finally traverse the right subtree. Second order traversal: first traverse the left subtree, then traverse the right subtree, and finally access the root node

non-recursive

In the non recursive operation, we still traverse the left subtree, then access the root node, and finally traverse the right subtree.

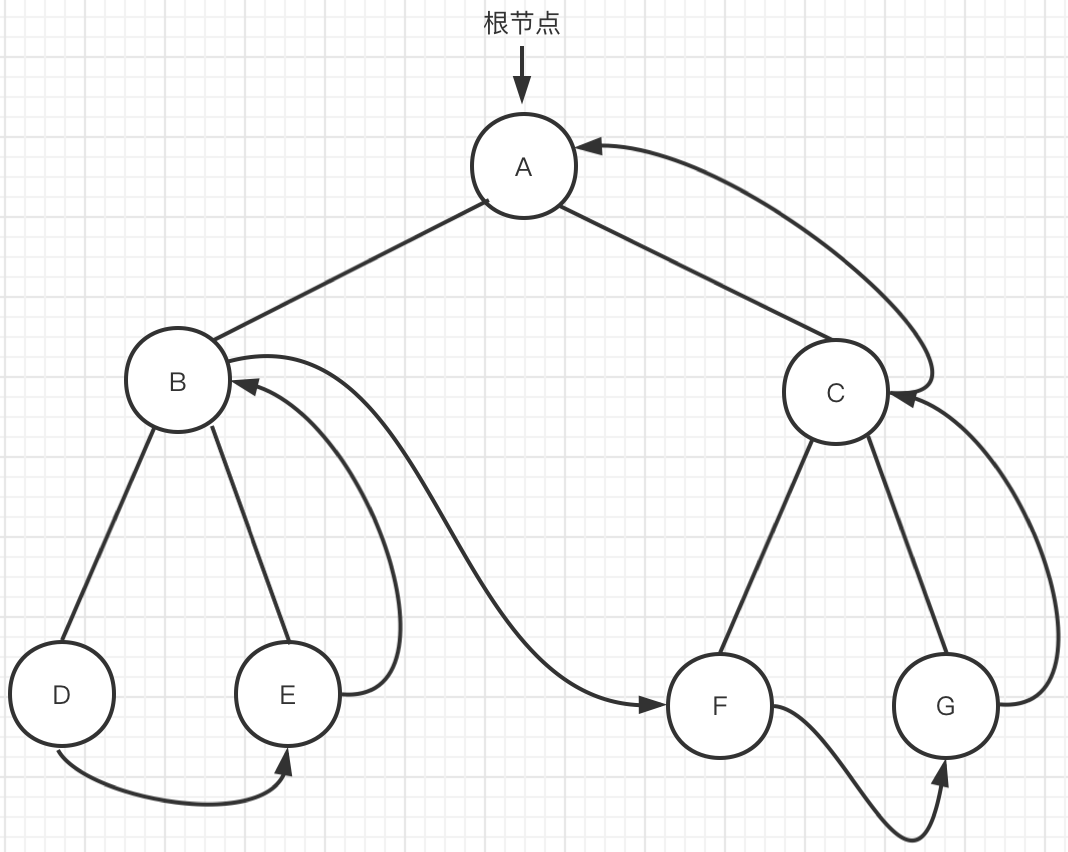
Figure 7 subsequent traversal

1. Reach node A and traverse the left subtree of A

2. Reach node B and traverse the left subtree of B

3. Node D is reached. Since D has no subtree, node D is accessed

   • Node D has no subtree, which means that the left subtree of node B is traversed, and then the right subtree of node B is traversed

4. Node e is reached. Since E has no subtree, node e is accessed

   • Node E has no subtree, which means that the right subtree of node B is traversed and connected back to node B

5. Access node B and return to root node A of node B

6. Reach node A and access the right subtree of node a

7. Reach node C and traverse the left subtree of node C

8. When reaching node F, since node f has no subtree, access node F

   • The access of node F is completed, which means that the traversal of the left subtree of node C is completed, so it returns to node C

9. Reach node C and traverse the right subtree of node C

10. Node G is reached because node G has no subtree because node G is accessed

• The access of node G is completed, which means that the traversal of the right subtree of node C is completed and returns to node C

1. Arrive at node C and access node C

• The traversal of node C is completed, which means that the traversal of the right subtree of node A is completed and returns to node A

1. After traversing the right subtree of node A, access node A

Traversing a binary tree in a non recursive way requires the introduction of additional data structure stacks. The basic process is as follows: 1. Apply for two stack stacks, and then press the header node into the specified stack.

2. Pop up the top node of the stack from the stack and put it into another stack

3. Press its left child node (if not empty) into the stack first

4. Press its right child node (if not empty) into the stack.

5. Repeat steps 2, 3 and 4 until the stack is empty.

6. Repeat access to another stack until the stack is empty

void PostOrder(TreeNode *root) {
  if (!root) {
    return;
  }
  
  std::stack<TreeNode*> s1;
  std::stack<TreeNode*> s2;
  
  s1.push(root);
  
  while (!s1.empty()) {
    auto t = s1.top();
    s1.pop();
    s2.push(t);
    
    if (t->left) {
      s1.push(t->left);
    }
    
    if (t->right) {
      s1.push(t->right);
    }
  }
  
  while (!s2.empty()) {
    auto t = s2.top();
    s2.pop();
    std::cout << t->val << std::endl;
  }
}

epilogue

For binary trees, the so-called traversal means that each node is accessed successively along a certain route, and each node is accessed only once. The traversal of binary tree is one of the common algorithms in the interview. We must understand it. When necessary, we need to recite it and even memorize it.