I problem

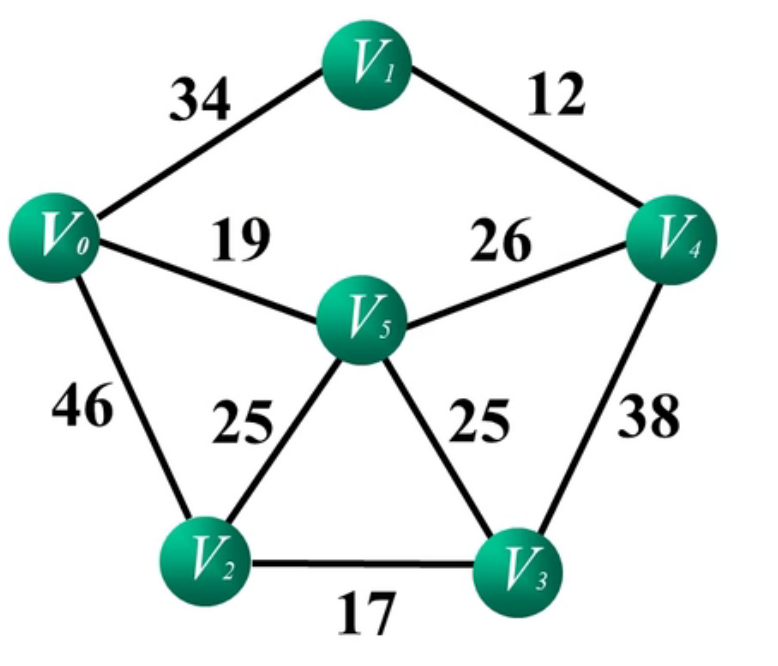
The six vertices in the figure represent six villages respectively, and the weight of the line segment represents the distance between villages. How can I find the shortest way to visit each village, and each village can only be visited once.

II solve

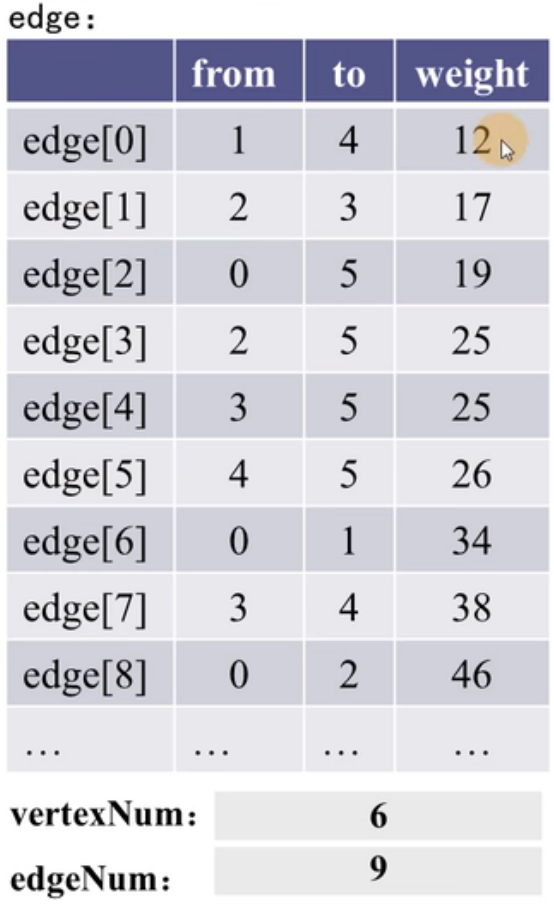
1. Extract the edges of the graph, arrange the edges from small to large according to the weight size, and put them into the edge array. As follows:

    

2. Create a root array (auxiliary array). The array subscript represents the vertex node itself, and its elements represent the root node of the vertex, as follows:

Tip: the "root" here is not the real root in the tree structure. There is only one root in a tree. The "root" here generally refers to the elders, which may be the parent node or the "master" node. The initialization root array is - 1, which means that each vertex represents a set in the initial state.

 3. Put the edges in the edge array back into the graph from small to large. If the subsequently added edges form a ring with the edges already placed in the graph, discard this edge and continue to put the next edge. The rules are the same as before.

Forming a ring means that the starting point and ending point of the added edge already belong to a set and have a common root. The process of adding edges is the continuous merging of multiple subsets, and the vertices in the same set cannot be connected. The preceding auxiliary array is used to determine whether the start point and end point belong to a set. See code comments for specific implementation.

 4. After putting (number of vertices - 1) edges, the construction of Minimum Spanning Tree is completed, and the cycle can be ended.

If a tree has n nodes, it has n-1 edges

III Details

The above algorithm mainly has two points to consider:

• Tree storage
• Representation of sets

Tree storage: common graph storage structures include adjacency matrix, adjacency edge table, cross linked list, adjacency multiple table and edge set array. Obviously, the above algorithms often involve the operation of opposite edges, so edge set array is the best choice.

Representation of a set: use an auxiliary array to store the root vertices of each vertex. If the roots of two vertices are the same, they belong to the same set, and the other is the opposite. The initialization auxiliary array element is - 1, which means that each vertex itself is the root node.

IV Realize

#include<iostream>
#define MAX_VEX  10
#define MAX_ Edge 100 / / an undirected graph composed of 10 vertices has up to 100 edges
#define TYPE int
using namespace std;

struct Edge  //Edge attribute structure
{
	TYPE start;
	TYPE end;
	TYPE weight;
};

void ini_gragh(int& vex, int& edge, Edge* gragh);//Using edge set array to store graphs

void sort_edge(Edge* edges,int edge);//Use bubble sorting to sort the edges from small to large according to the weight size

int find_root(int parent[], int n);//Find the root node to determine whether it is in a collection


int main()
{
	int vex; //Number of vertices

	int edge; //Number of edges

	Edge gragh[MAX_EDGE];

	ini_gragh(vex, edge, gragh);//Edge set array initialization graph

	sort_edge(gragh, edge);//The edges are sorted from small to large according to the weight

	int roots[MAX_VEX];  //Root array, which stores the root node of each vertex to distinguish whether it belongs to the same set

	Edge MST[MAX_EDGE];   //minimum spanning tree

	int count = 0;  

	for (int i = 0; i < vex; i++)
		roots[i] = -1;  //Initialize the root array, - 1 means you are the root node; In the initial state, each vertex is an independent root

	for (int i = 0; i < MAX_EDGE; i++)
	{
		int vex_m = find_root(roots, gragh[i].start);//Find the root node of the starting point
		int vex_n = find_root(roots, gragh[i].end);//Find the root node of the end point

		if (vex_m != vex_n)//If the root nodes of the two are different, they belong to different sets and can be connected
		{
			MST[count] = gragh[i];//Put this edge into the MST array
			count++;
			roots[vex_m] = vex_n;//Merge the two trees, that is, vertex vex_n as vex_ Root node of M
		}
		if (count == vex-1)//When the count reaches - 1, it indicates that the minimum tree has been generated and exits the cycle
			break;
	}

	for (int i = 0; i < vex - 1; i++)
	{
		printf("(%d,%d)%d\n", MST[i].start, MST[i].end, MST[i].weight);   //Print minimum spanning tree
	}
	return 0;
}

void ini_gragh(int& vex, int& edge, Edge* gragh)
{
	cout << "Enter the number of connected network vertices:";
	cin >> vex;
	cout << "Enter the number of connected network edges: ";
	cin >> edge;
	cout << "Enter the start point, end point and weight of each edge in turn(Space separated): " << endl;
	for (int i = 0; i < edge; i++)
	{
		cin >> gragh[i].start >> gragh[i].end >> gragh[i].weight;
	}
}

void sort_edge(Edge* edges_arr,int edge)
{
	Edge temp;	
	for (int i = 0; i < edge; i++)
	{
		for (int k = 0; k < edge - i - 1; k++)//Bubble sort. Note that 1 should be subtracted here
		{
			if (edges_arr[k].weight > edges_arr[k + 1].weight)
			{
				temp = edges_arr[k];
				edges_arr[k] = edges_arr[k + 1];
				edges_arr[k + 1] = temp;
			}
		}
	}
}

int find_root(int roots[], int n)
{
	while (roots[n] > -1)  //Iteratively find the root node
		n = roots[n];
	return n;
}

Operation results: