Change
The most direct solution to the change problem is the greedy strategy.
For example: for coins with face values of 1, 5, 10 and 25, solve the minimum number of coins required to exchange 63 yuan.
The idea of greedy strategy is to constantly use the coins with the largest face value to try. No, in this case, 25 coins are used to try the coins with smaller face value. After two 25 coins, 13 yuan is left, one coin with the face value of 10 is used, and finally three coins with the face value of 1 yuan are used. Therefore, the minimum number of coins is 6. This idea is also similar to the balance experiment in middle school, constantly trying to balance the balance with larger weights.
However, the greedy strategy has obvious disadvantages. Giving priority to the coins with the largest face value may not achieve the best result. In this example, if there is a face value of 21 yuan, the optimal solution should be three coins with 21 face value instead of six.
Next, we use the idea of recursion to solve the problem of change.
Recursive solution
The core idea of recursive solution:
The idea of recursion is actually similar to the concept of interrupt when we learn MCU. The three most important links in interrupt are entering breakpoint, executing interrupt subroutine and breakpoint recovery. The difference is that the subroutine called recursively is itself that keeps shrinking. Therefore, each call itself will enter a smaller subroutine, execute the smaller subroutine, and return the upper subroutine with a larger scale until it returns to the main program and continues to execute the main program. The breakpoint recovery here actually uses the concept of stack. After entering the breakpoint every time, press the breakpoint into the stack, and pop up the breakpoint from the top of the stack when the breakpoint is recovered.
Therefore, to complete a recursive operation, several conditions are required:
1. The problem has the same problem on a smaller scale
2. For the problem with the smallest scale, there are appropriate end conditions. The subroutine cannot be called continuously, otherwise it cannot always return
3. Recursion can evolve to the smallest problem
Change ideas:
1. Large change problems can be decomposed into smaller change problems.
2. There is a minimum solution to the change problem, that is, the minimum face value of the coin is equal to the face value. Return the number of coins 1 and end the minimum scale subroutine
3. It can make the subroutine evolve to the minimum scale problem by continuously reducing the scale
Therefore, recursion can be used to solve the problem, and the most important problem is to solve how to indent the scale. The face value reduction method can be used as follows [in the case of face values of 1, 5, 10 and 25]:

The procedure is as follows:
def recMc(coinValueList, change):
'''
Change problem complex version
:param coinValueList: Face value list
:param change: money
:return: Minimum number of coins
'''
minCoins = change
if change in coinValueList:
return 1
else:
for i in [c for c in coinValueList if c <= change]:
numCoins = 1 + recMc(coinValueList, change - i)
if numCoins < minCoins:
minCoins = numCoins
return minCoins
This is the most basic recursive method, but its shortcomings are obvious. There are too many repeated calculations. For example, the minimum number of coins of a smaller scale has been calculated, but in the process of recursion from the superior, it is still calling down, resulting in extremely low efficiency. On my computer, the program takes 18 seconds to get the result.
How to solve the problem of double counting?
Recursive method of adding recorder
The simplest way is to calculate the number of coins of a smaller scale and record it in a list. The next time you recurse to the face value, you can directly look up the table to get the solution of the scale problem and return it, so as to avoid deeper calls.
The procedure is as follows:
def recMc_pro(coinValueList, change, knownResults):
'''
The improved version of change problem uses a list to store the solutions of sub problems and avoid repeated recursive calls
:param coinValueList: Face value list
:param change: money
:return: Minimum number of coins
'''
minCoins = change
if change in coinValueList:
knownResults[change] = 1 # Record the optimal solution
return 1
elif knownResults[change] > 0:
return knownResults[change] # Look up the table successfully and use the optimal solution directly
else:
for i in [c for c in coinValueList if c <= change]:
numCoins = 1 + recMc_pro(coinValueList, change - i, knownResults)
if numCoins < minCoins:
minCoins = numCoins
# Find the optimal solution and record it in the table
knownResults[change] = minCoins
return minCoins
The improved recursive method greatly speeds up the operation of the program, and only needs 200 times of recursion to return the optimal solution
Dynamic programming solution
The idea of dynamic programming:
Different from the recursive method, recursion decomposes the big problem into small problems, and finally returns the solution of the big problem step by step. Dynamic programming starts from the smallest problem and directly kills the big problem by constantly solving small problems.
For example, the change problem: assuming that the face value table is [1, 5, 10, 25], you need to exchange 11 yuan.
Then, starting from the smallest problem, when you exchange 1 yuan, you need at least one 1 yuan coin, and when you exchange 2 yuan, you need two 1 yuan coins. Similarly, when you exchange 3 yuan and 3 yuan, you can exchange 4 yuan and 4 yuan. When you exchange 5 yuan, you can use at least one 5 yuan coin, at least one 5 yuan coin and one 1 yuan coin for 6 yuan... So as to establish a change exchange table, Any exchange result can be obtained by referring to the table.
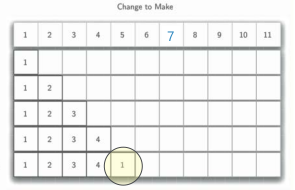
The procedure is as follows:
def dynamic(change_list, change):
"""
Dynamic programming method to solve the problem of change
:param change_list: Face value table, as in this example[1, 5, 10, 21, 25]
:param change: money
:return: Minimum amount of change
"""
# Create a record table with the length of change + 1
record_list = [0] * (change + 1)
for change in range(1, change+1):
# The change number is recorded in the table and the number of coins 1 is returned
if change in change_list:
record_list[change] = 1
else:
# If it is not in the table, check the last minimum number of coins, subtract the last change value, check the table again, and add the number of coins
# A cache is created to avoid testing with cent = 1 only
temp = []
# For circular calculation, it is necessary to prevent the cent from exceeding the current change, otherwise it will appear that it cannot be found in the table
for cent in [cents for cents in change_list if cents <= change]:
last_num = record_list[change - cent]
temp.append(last_num + record_list[cent])
record_list[change] = min(temp)
# wipe cache
temp.clear()
return record_list[change]
The core idea is still the previous formula. Here, a caching technique is introduced to store the optimal quantity corresponding to each face value and obtain the optimal result for the current change. In general, it is to maintain the optimal solution of each face value in the record table. How can we add fewer results by constantly looking at the table when calculating the results.
For self-study records, refer to Professor Chen Bin's tutorial on data structure and analysis in python. The link is as follows: