Article catalog

1.1 algorithm efficiency

There are two kinds of algorithm efficiency analysis: the first is time efficiency and the second is space efficiency. Time efficiency is called time complexity,
Spatial efficiency is called spatial complexity. The time complexity mainly measures the running speed of an algorithm, while the space complexity mainly measures the speed
To measure the extra space required by an algorithm, in the early days of computer development, the storage capacity of computers was very small. So for space
Complexity matters. However, with the rapid development of computer industry, the storage capacity of computer has reached a high level.
Therefore, we no longer need to pay special attention to the spatial complexity of an algorithm.

1.2 concept of time complexity

Definition of time complexity: in computer science, the time complexity of an algorithm is a function that quantitatively describes the operation of the algorithm
Line time. In theory, the time spent in the execution of an algorithm cannot be calculated. Only you put your program on the computer
You can't know until you run on the machine. But do we need every algorithm to be tested on the computer? Yes, they can all be tested on the computer, but it's very numb
Annoying, so there is the analysis method of time complexity. The time taken by an algorithm is directly proportional to the number of executions of the statements in it
For example, the execution times of basic operations in the algorithm is the time complexity of the algorithm. (it doesn't depend on the time. The program operation is also related to hardware equipment, etc.)

1.3 concept of spatial complexity

Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation. Space complexity is not occupied by the program
How many bytes of space is used, because it doesn't make much sense, so the space complexity is the number of variables. Spatial complexity meter
The computational rules are basically similar to the practical complexity, and the large O progressive representation is also used.

Asymptotic representation of large O

// Please calculate how many times the Func1 basic operation is executed?
void Func1(int N)
{
  int count = 0;
  for (int i = 0; i < N ; ++ i)
  {
     for (int j = 0; j < N ; ++ j)
     {
           ++count;
     }
  }
  for (int k = 0; k < 2 * N ; ++ k)
  {
      ++count;
  }
  int M = 10;
  while (M--)
  {
      ++count;
  }
  printf("%d\n", count);
  return 0;
}

Number of basic operations performed by Func1:

F(N)=N*N+2*N+10;

N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010

In fact, when we calculate the time complexity, we do not have to calculate the exact number of executions, but only about one execution
Number, then here we use the asymptotic representation of large O.

Big O notation: a mathematical symbol used to describe the asymptotic behavior of a function.

Derivation of large O-order method:
1. Replace all addition constants in the run time with constant 1.
2. In the modified run times function, only the highest order term is retained.
3. If the highest order term exists and is not 1, the constant multiplied by this item is removed. The result is large O-order.

After using the asymptotic representation of large o, the time complexity of Func1 is O(N^2)

The progressive representation of big O removes the items that have little impact on the results, and succinctly and clearly shows the persistence
Number of rows.

Let's practice:

// Calculate the time complexity of Func2?
void Func2(int N)
{
  int count = 0;
  for (int k = 0; k < 2 * N ; ++ k)
  {
    ++count;
  }
  int M = 10;
  while (M--)
  {
   ++count;
  }
  printf("%d\n", count);
}

The basic operation is performed 2N+10 times. It is known that the time complexity is O(N) by deriving the large O-order method

// Calculate the time complexity of Func3?
void Func3(int N, int M)
{
  int count = 0;
  for (int k = 0; k < M; ++ k)
  {
    ++count;
  }
  for (int k = 0; k < N ; ++ k)
  {
    ++count;
  }
  printf("%d\n", count);
  return 0；
}

The basic operation is executed M+N times, there are two unknowns M and N, and the time complexity is O(N+M)

In addition, the time complexity of some algorithms has the best, average and worst cases:

Worst case: maximum number of runs of any input scale (upper bound)
Average case: expected number of runs of any input scale
Best case: minimum number of runs of any input scale (lower bound)

For example, search for a data x in an array of length N
Best case: 1 time
Worst case: found N times
Average: N/2 times

In practice, we usually focus on the worst-case operation of the algorithm, so the time complexity of searching data in the array is O(N)

Let's practice:

// Calculate the time complexity of BinarySearch?
int BinarySearch(int* a, int n, int x)
{
  assert(a);
  int begin = 0;
  int end = n;
  while (begin < end)
  {
    int mid = begin + ((end-begin)>>1);
    if (a[mid] < x)
      begin = mid+1;
    else if (a[mid] > x)
      end = mid;
    else
      return mid;
  }
  return -1;
}

The best and worst basic operations are performed once, and the time complexity is O(logN) ps: logN in algorithm analysis
In, the base is 2 and the logarithm is N. Some places will be written as lgN.  

The idea is as follows:

Discrimination Title: as follows

// The time complexity of computing Factorial recursive Factorial?
long long Factorial(size_t N)
{
  return N < 2 ? N : Factorial(N-1)*N;
}

How to calculate the recursive algorithm: the number of recursions * the number of recursive functions each time. So the answer is O(N)

Idea: to calculate N, you need to add 1 to N-1; To calculate N-1, you need to add 1 to N-2. Strictly speaking, we should recurse N times from N to 1

 

----------------------------------------------------------------------------------------------------------------------------- 

// Time complexity of computing Fibonacci recursive Factorial?
long long Factorial(size_t N)
{
  return N < 2 ? N : Factorial(N-1)*Factorial(N-2);
}

Drawing analysis:

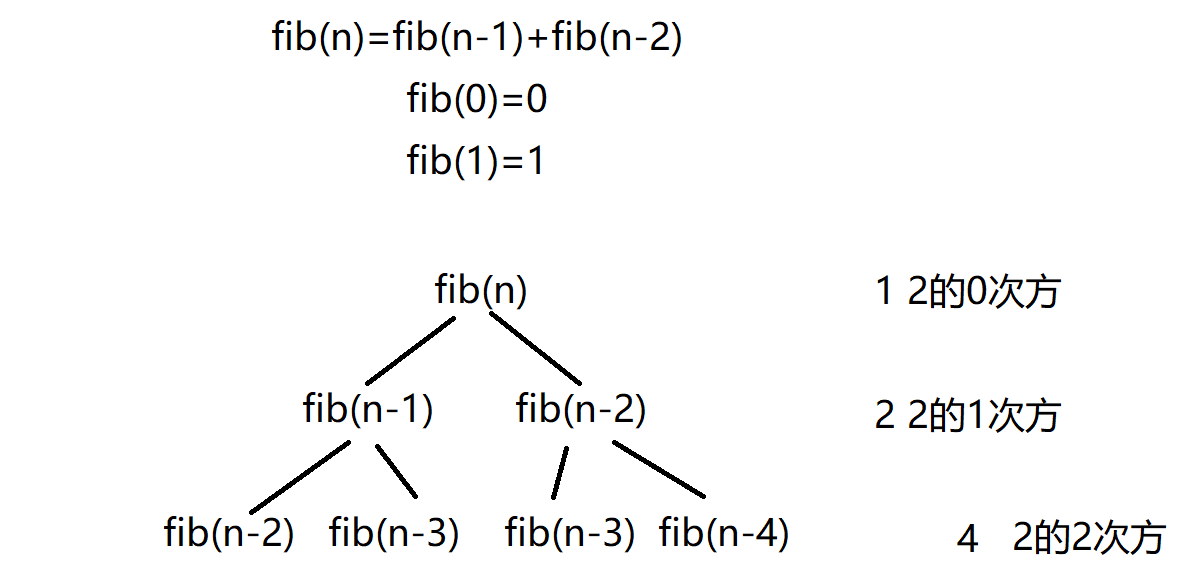
2^0+2^1+2^2+..............+2^(n-1)=2^n-1

The time complexity does not calculate the time, but the approximate number of operations

Space complexity does not calculate the space, but the number of roughly defined variables

Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation. Space complexity is not occupied by the program
How many bytes of space is used, because it doesn't make much sense, so the space complexity is the number of variables. Spatial complexity meter
The calculation rules are basically similar to the practical complexity, and the large O progressive representation is also used

//Calculate the spatial complexity of BubbleSort?
void BubbleSort(int* a, int n)
 {
 assert(a);
 for (size_t end = n; end > 0; --end)
 {
   int exchange = 0;
   for (size_t i = 1; i < end; ++i)
   {
      if (a[i-1] > a[i])
      {
        Swap(&a[i-1], &a[i]);
        exchange = 1;
      }
   }
   if (exchange == 0)
       break;
  }
}

// Calculate the spatial complexity of Fibonacci?
long long* Fibonacci(size_t n)
{
  if(n==0)
     return NULL;
  long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
  fibArray[0] = 0;
  fibArray[1] = 1;
  for (int i = 2; i <= n ; ++i)
  {
     fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];
  }
  return fibArray ;
}

// Calculate the spatial complexity of Factorial recursive Factorial?
long long Factorial(size_t N)
{
 return N < 2 ? N : Factorial(N-1)*N;
}

1. Example 1 uses two additional spaces, so the space complexity is O(1)
2. Example 2 dynamically opens up N spaces with a space complexity of O(N)
3. Instance 3 recursively called N times, opened up N stack frames, and each stack frame used a constant space. Space complexity is O(N)

 

summary

The time complexity does not calculate the time, but the approximate number of operations

Space complexity does not calculate the space, but the number of roughly defined variables