catalogue
1, Concept definition
According to the definition, time complexity refers to the time required for the algorithm to run when the input data size is N +. Note:
It counts the "number of calculation operations" of the algorithm, not the "absolute time of operation". There is a positive correlation between the number of calculation operations and the absolute running time, which is not equal.
The running time of the algorithm is affected by [programming language, computer processor speed, running environment] and other factors. For example, when the same algorithm is implemented in Python or C + +, CPU or GPU, local IDE or OJ platforms such as Luogu and likuo, the running time is different.
It reflects the change of calculation operation with the change of data size n #. Assuming that the algorithm needs "1 operation" and "100 operations" in total, the time complexity of these two cases is constant level O(1). The time complexity of "n operations" and "100N operations" is O(N).
2, Symbolic representation
According to the characteristics of the input data, the time complexity can be divided into [worst], [average] and [best], using O respectively, Θ , Ω is represented by three symbols.
The following is an example topic of search algorithm to help understand.
subject: The input length is N Array of integers nums,Determine whether there is the number 8 in this array,
Return if any true ,Otherwise return false.
Problem solving algorithm: linear search, that is, traverse the entire array, and return when encountering 8 true.
code:
bool findEight(vector<int>& nums) {
for (int num : nums) {
if (num == 8)
return true;
}
return false;
}1) Best case Ω (1): num = [8, a, B, C,...], That is, when the first number of the array is 8, no matter how many elements num has, the number of cycles of linear search is 1;
2) Worst case O(N): num = [a, B, C,...] And all numbers in nums are not 8. At this time, the linear search will traverse the whole array and cycle N times;
3) Average situation Θ : It is necessary to consider the distribution of input data and calculate the average time complexity under all data conditions; For example, in this topic, we need to consider the array length, the value range of array elements, etc;
Note: Big O is the most commonly used progressive symbol for time complexity evaluation.
3, Common species
According to the arrangement from small to large, the common algorithm time complexity mainly includes:
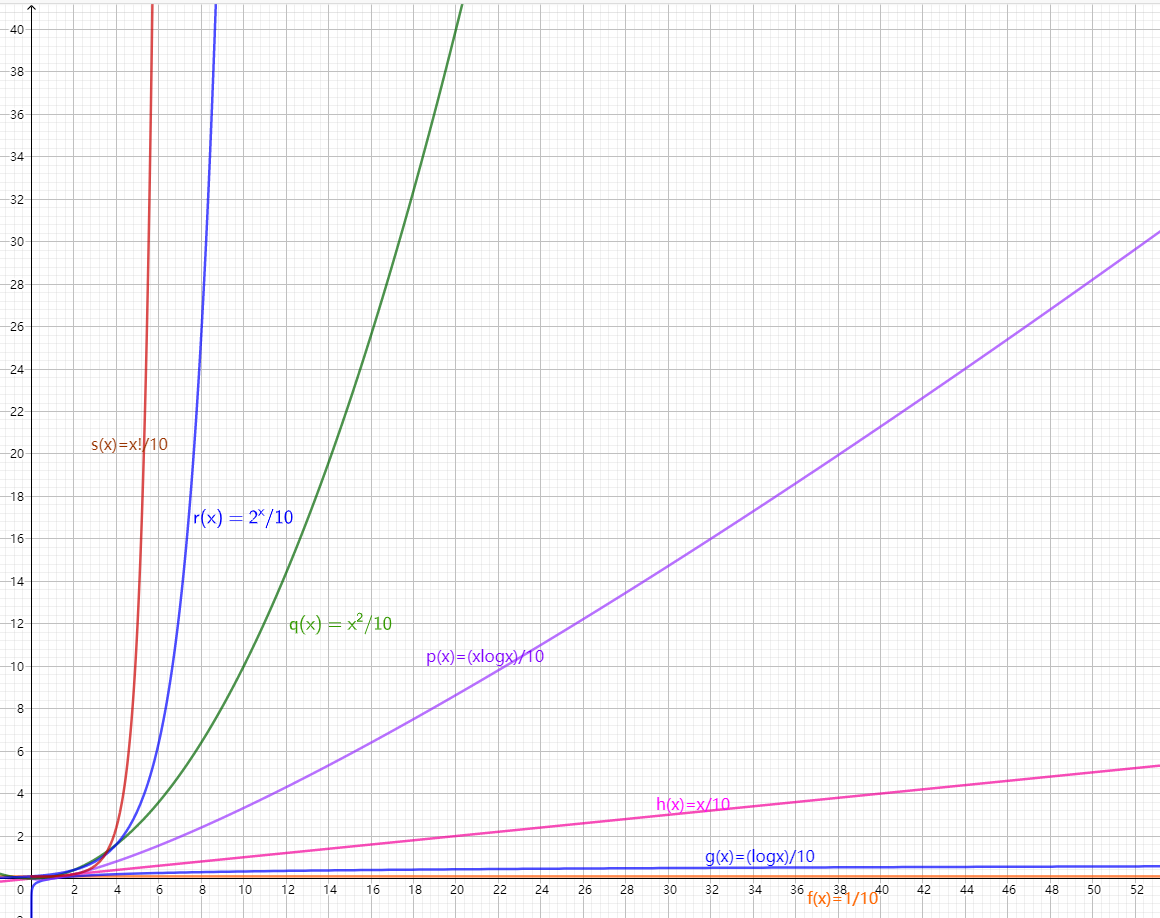
O(1) < O(logN) < O(N) < O(NlogN) < O(N^2) < O(2^N) <O(N!)
As shown in the figure:
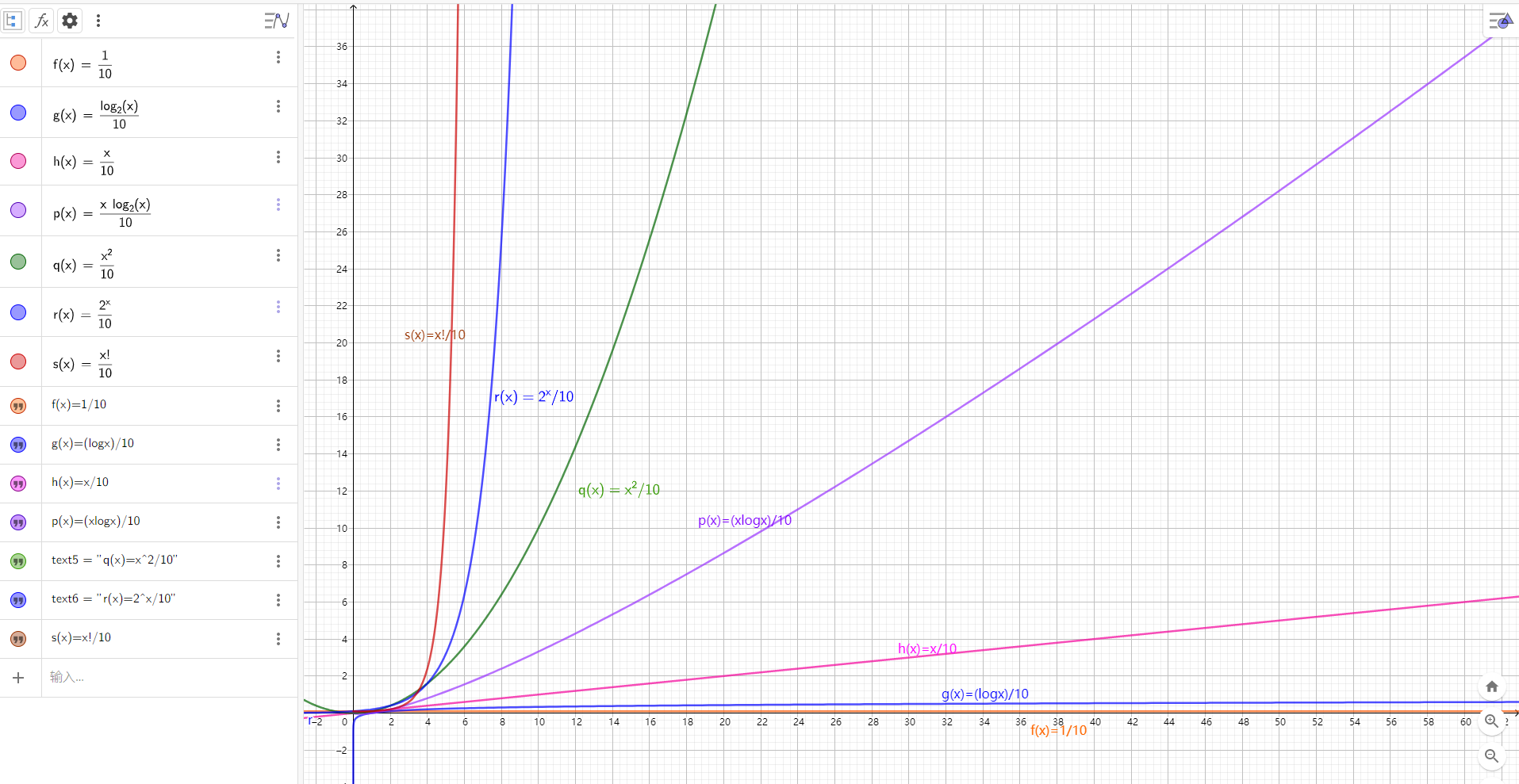
Large picture:
4, Sample parsing
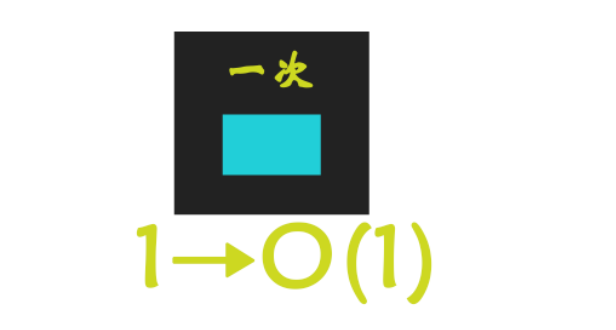
For all the following examples, set the input data size to N and the number of calculation operations to count. Each "blue square" in the figure represents a unit calculation operation.
1. Constant O(1)
The number of runs has a constant relationship with the size of N, that is, it does not change with the change of the input data size n. For example:
int algorithm(int N) {
int a = 1;
int b = 2;
int x = a * b + N;
return 1;
}For the following code, no matter how large a , is, it has nothing to do with the input data size N, so the time complexity is still O(1).
int algorithm(int N) {
int count = 0;
int a = 10000;
for (int i = 0; i < a; i++) {
count++;
}
return count;
}
2. Linear O(N)
There is a linear relationship between the number of cycles and the size of N, and the time complexity is O(N).
int algorithm(int N) {
int count = 0;
for (int i = 0; i < N; i++)
count++;
return count;
}
For the following code, although it is a two-layer cycle, the second layer has nothing to do with the size of N ^ so the whole is still linear with N ^.
int algorithm(int N) {
int count = 0;
int a = 10000;
for (int i = 0; i < N; i++) {
for (int j = 0; j < a; j++) {
count++;
}
}
return count;
}3. Square O(N^2)
The two layers of cycles are independent of each other and have a linear relationship with ^ so the overall relationship with ^ N ^ is square, and the time complexity is ^ O(N^2).
int algorithm(int N) {
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
count++;
}
}
return count;
}Take "bubble sorting" as an example, which includes two independent loops:
The complexity of the first layer is O(N);
The average number of cycles of the second layer is O(N/2), and the complexity is O(N). The derivation process is as follows:
O(N/2) = O(1/2)O(N) = O(1)O(N) = O(N)
Therefore, the overall time complexity of bubble sorting is O(N^2), and the code is as follows.
vector<int> bubbleSort(vector<int>& nums) {
int N = nums.size();
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < N - 1 - i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums[j], nums[j + 1]);
}
}
}
return nums;
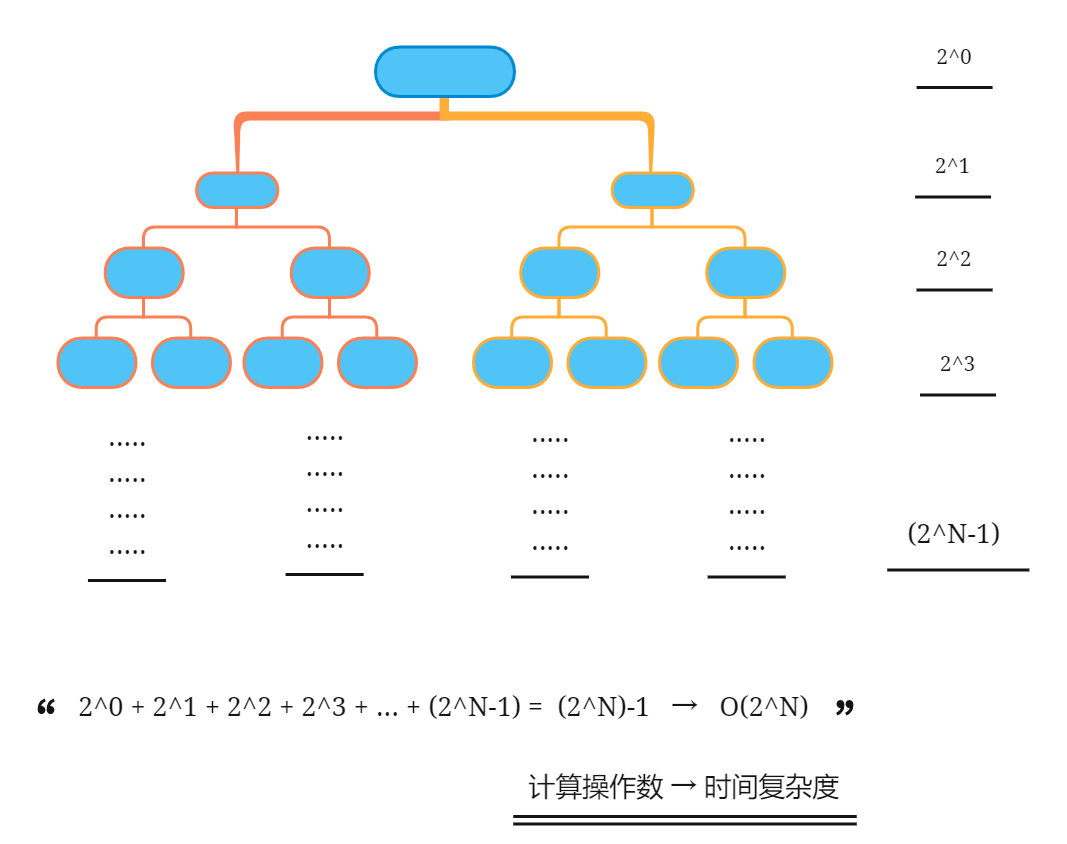
}4. Index O(2^N)
"Cell division" in biology is exponential growth. The initial state is 1 ^ N cells, 2 after one round of division, 4 after two rounds of division,..., and 2^N cells after N rounds of division.
In the algorithm, exponential order often appears in recursion. The schematic diagram and code of the algorithm are as follows.
int algorithm(int N) {
if (N <= 0) return 1;
int count_1 = algorithm(N - 1);
int count_2 = algorithm(N - 1);
return count_1 + count_2;
}
5. Factorial O(N!)
Factorial order corresponds to the common "total arrangement" in mathematics. That is, given N non repeating elements, find all possible arrangement schemes, and the number of schemes is:
N×(N−1)×(N−2)×⋯×2×1=N!
As shown in the figure below and the code, factorial is often implemented recursively. The algorithm principle: the first layer splits N, the second layer splits N - 1,... Until it reaches the nth layer and terminates and backtracks.
int algorithm(int N) {
if (N <= 0) return 1;
int count = 0;
for (int i = 0; i < N; i++) {
count += algorithm(N - 1);
}
return count;
}
6. Log O(logN)
The logarithmic order is opposite to the exponential order, which is "the case of splitting twice in each round", while the logarithmic order is "the case of excluding half in each round". Logarithmic order often appears in "dichotomy", "divide and conquer" and other algorithms, reflecting the algorithm idea of "one is divided into two" or "one is divided into many".
If the number of cycles is m, the input data size N has a linear relationship with 2^m, and the logarithm of log(2, N) is taken on both sides at the same time, then the number of cycles m has a linear relationship with log(2, N), that is, the time complexity is O(logN).
int algorithm(int N) {
int count = 0;
float i = N;
while (i > 1) {
i = i / 2;
count++;
}
return count;
}
As shown in the following code, for different values of a, the number of cycles m has a linear relationship with log (a,N), and the time complexity is O (log (a,N)). Regardless of the value of base a, the time complexity can be recorded as O(logN). According to the derivation of logarithm base exchange formula, it is as follows:
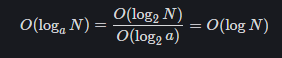
int algorithm(int N) {
int count = 0;
float i = N;
int a = 3;
while (i > 1) {
i = i / a;
count++;
}
return count;
}7. Linear logarithm O(N*logN)
The two layers of loops are independent of each other. The time complexity of the first layer and the second layer are O(logN) and O(N) respectively, so the overall time complexity is O(NlogN);
int algorithm(int N) {
int count = 0;
float i = N;
while (i > 1) {
i = i / 2;
for (int j = 0; j < N; j++)
count++;
}
return count;
}Linear logarithmic order often appears in sorting algorithms, such as "quick sort", "merge sort", "heap sort", etc. its time complexity principle is shown in the figure below.

I'm classmate Lu. I wish myself and you become stronger ~