catalogue
6. Heap sorting
Learning heap sorting has to introduce the types of binary trees. Binary trees are divided into complete binary trees, balanced binary trees, ordered binary trees, full binary trees and perfect binary trees. It can be considered that heap sorting is a sort algorithm designed by using the structure of complete binary tree. The sequence number of the complete binary tree corresponds to the array as follows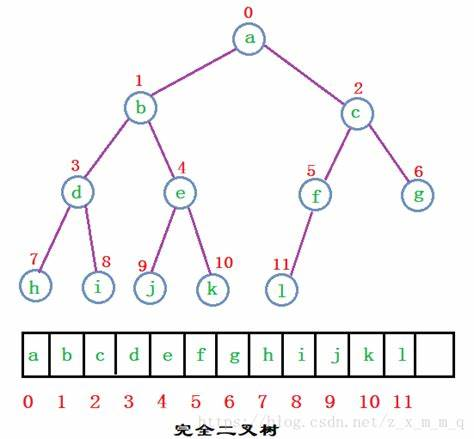
Algorithm steps
1. First form a large root heap, and the value of the root node is greater than that of the child node;
2. Then exchange the first number in the sequence with the last number. The last number will be the maximum value. The length of the sorting sequence will be reduced by 1 and the heap length will be reduced by 1;
3. Repeat 1, 3 until the sort sequence is 1.
The idea of forming large root heap: insert the rising method, traverse each element and compare it with its parent node. Time complexity O(nlog(n)).
heapify operation, with the help of the characteristics of the original large root heap, top down method and time complexity O(logn).
The overall time complexity of the algorithm is O(nlog(n)), and the spatial complexity is O(1). instable.
```Java
public static int[] sortHeap(int[] a){
int len=a.length;
//Get big root pile
MaxHeap(a,len);
//Swap once, and the heap length is reduced by 1
for(int i=len-1;i>0;i--){
swap(a,0,i);
len--;
heapify(a,0,len);
}
return a;
}
//Here, we have to use the top down method to generate the characteristic complexity log(n) of the large root heap for the first time
private static void heapify(int[] a, int i, int len) {
int left=2*i+1;
int right=2*i+2;
while (left<len){
int largeIndex;
//Compare the size of child nodes. When the right node is empty, the left node is the largest
if(right<len&&a[left]<a[right]){
largeIndex=right;
}else{
largeIndex=left;
}
//Compare with root node
if(a[i]<a[largeIndex]){
swap(a,i,largeIndex);
i=largeIndex;
}else {
break;
}
left=2*i+1;
right=2*i+2;
}
}
private static void swap(int[] a, int i, int j) {
int temp=a[i];
a[i]=a[j];
a[j]=temp;
}
//Insertion rising complexity nlog(n)
private static void MaxHeap(int[] a, int length) {
for(int i=0;i<length;i++){
int index=i;
while (a[index]>a[(index-1)/2]){
swap(a,index,(index-1)/2);
index=(index-1)/2;
}
}
}
```7. Quick sort
Quick sort uses divide and conquer strategy to divide a serial into two subseries. In essence, it seems to be a recursive divide and conquer method based on bubble sort. Compared with bubble, the exchange interval becomes larger and the speed becomes faster. Next, I will introduce three versions of fast platoon, namely version 1.0, version 2.0 and version 3.0. The core of fast scheduling is partition operation.
partition: divide a sequence into three parts, with a number less than or equal to the left, greater than or equal to the right, and equal to the middle. This is the famous Dutch flag problem. The additional space complexity is O(1) and the time complexity is O(n).
Algorithm steps:
1. Select the last number of the sequence as the division value, and define 2 numbers as the left boundary of the less than area and the right boundary of the greater than area;
2. Number traversal starts from the first one. The number less than or equal to the partition value is exchanged with the number less than the next number in the area, which is less than the right expansion of the area, and the number greater than the partition value is exchanged with the number greater than the previous number in the area, which is greater than the right expansion of the area. Equal to the partition value, traverse the next number;
3. The partition value is exchanged with the first number greater than the area.
```Java
public static int[] partition(int[]a,int L,int R){//50. R is 0 and length-1
int less=L-1;//Less than the right boundary of the area
int more=R;//Greater than the left boundary of the area
while(L<more){
if(a[L]<a[R]){
swap(a,++less,L++);
}else if(a[L]>a[R]){
swap(a,--more,L);
}
else if(a[L]==a[R]){
L++;
}
}
swap(a,more,R);
//Return the position of the divided value after exchange and the position of the next data less than the area, the middle area
return new int[]{less++,more};
}
```7.1 fast exhaust 1.0
Algorithm steps:
1. partition the unordered sequence;
2. Then perform the partition operation in the less than or equal area and greater than area respectively.
```Java
public static int[] sortQuick1(int[] a,int L,int R){
if(L>=R){
return a;
}
int[] b=partition(a, L, R);
sortQuick1(a,L,b[1]-1);
sortQuick1(a,b[1]+1,R);
return a;
}
```7.2 fast exhaust 2.0
Compared with fast scheduling 1.0, step 2 of the algorithm becomes to perform partition operation in less than area and equal to area. Faster than 1.0.
```Java
public static int[] sortQuick2(int[] a,int L,int R){
if(L>=R){
return a;
}
int[] b=partition(a, L, R);
sortQuick2(a,L,b[0]-1);
sortQuick2(a,b[1]+1,R);
return a;
}
```7.3 fast exhaust 3.0
The worst time complexity of fast platoon 1.0 and fast platoon 2.0 reaches (the partition value is the maximum or minimum value) O(n2), and fast platoon 3.0 randomly divides the value for partition operation.
```Java
public static int[] sortQuick3(int[] a,int L,int R){
if(L>=R){
return a;
}
//Randomly generate partition value and exchange with the last number
swap(a,L+(int)(Math.random()*(R-L+1)),R);
int[] b=partition(a, L, R);
sortQuick3(a,L,b[0]-1);
sortQuick3(a,b[1]+1,R);
return a;
}
```7.4 summary
1. Time complexity O(n2) of fast platoon 1.0 and fast platoon 2.0;
2. Fast scheduling 3.0 time complexity O(logn);
3. The spatial complexity is O(logn);
4. Instability
5. If sorting wants to run fast, use fast sorting, with low average complexity;
6. If you want less space, use stacking;
7. If you want to have stability, choose merging and sorting;
8. Sorting based on comparison cannot achieve time complexity O(n);
| Time complexity | Spatial complexity | stability | |
| choice | N2 | 1 | instable |
| Bubbling | N2 | 1 | stable |
| Merge | NlogN | N | stable |
| insert | N2 | 1 | stable |
| Quick row | NlogN | logN | instable |
| Stack row | NlogN | 1 | instable |