1. Preface

Cut point and bridge, a branch of graph theory, are often implemented by Tarjan algorithm.

Yes, it's this algorithm again

Note that the implementation of Tarjan algorithm in cut point and bridge is different from that in strong connected component.

Pre knowledge:

• dfs tree / dfs order

2. Cutting point

Example: P3388 [formwork] cutting point (cutting top)

2.1 definitions

Definition of cut point: in a graph, if the number of connected blocks increases after deleting a point, then this point is the cut point of the graph.

For example, in the following figure, point 4 is the cut point.

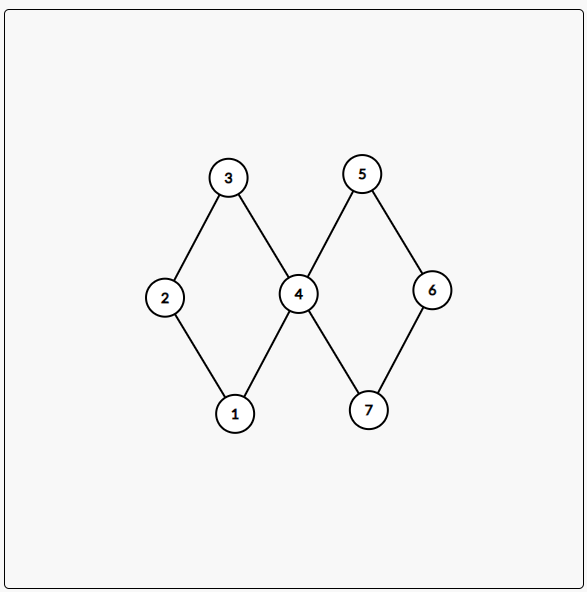
It should be noted that a graph may have multiple cut points.

2.2 calculation method

So how to find the cut point?

Using dfs to find the cut point, it is obvious that there will be a dfs order and a dfs tree.

Record two values during the process d f n , l o w dfn,low dfn,low. d f n dfn dfn indicates that this point is the first to be accessed in dfs. The special term is time stamp. l o w low low indicates the point with the smallest timestamp that this point can return to without passing through the parent node in its dfs tree. Initial value l o w = d f n low=dfn low=dfn.

So for an edge ( u , v ) (u,v) (u,v) (specified here in dfs tree) u u u is v v v's father), if l o w v > = d f n u low_v>=dfn_u lowv > = dfnu, then at this moment u u u is the cut point because v v v except after u u u can't come again u u The point above u is too high.

How to update l o w low What about low?

For the current point n o w now now, set its next strike point as u u u. There are two cases:

• u u u has not been passed.
  This time we go to u u u continue dfs. Order after dfs l o w n o w ← min ⁡ ( l o w n o w , l o w u ) low_{now} \leftarrow \min(low_{now},low_u) Low ← min (low, low U), because u u u can reach n o w now now must be there.
• u u u was passed.
  Update directly at this time l o w n o w ← min ⁡ ( l o w n o w , d f n u ) low_{now} \leftarrow \min(low_{now},dfn_u) Low ← min (low, dfnu) is enough, because at this time n o w now now went to the father node without passing by u u u.

It should be noted that the second case is not handled separately in the code. The specific reason is that for any point u u u， d f n u ≥ l o w u dfn_u \geq low_u dfnu​≥lowu​.

Therefore, in essence, if it is the first case, update l o w n o w ← min ⁡ ( l o w n o w , d f n u ) low_{now} \leftarrow \min(low_{now},dfn_u) Low ← min (low, dfnu) is invalid.

The algorithm is clear and the correctness is obvious, but there is one point we haven't dealt with.

What about the node at the beginning of dfs?

This node is the root node in the dfs tree. The timestamp of this point is the smallest, so it can't be smaller.

Therefore, for this point, the judgment method is: when it enters the next layer of dfs no less than 2 times, this point is the cut point.

Because if the root node is deleted at this time, there will be at least one more connected block because it recurses down at least twice. By definition, this point is a cut point.

Now everything is handled.

code:

/*
========= Plozia =========
    Author:Plozia
    Problem:P3388 [Template] cutting point (cutting top)
    Date:2021/5/10
========= Plozia =========
*/

#include <bits/stdc++.h>

typedef long long LL;
const int MAXN = 2e4 + 10, MAXM = 1e5 + 10;
int n, m, Head[MAXN], cnt_Edge = 1, dfn[MAXN], Low[MAXN], cnt_node;
struct node { int to, Next; } Edge[MAXM << 1];
bool book[MAXN];

int read()
{
    int sum = 0, fh = 1; char ch = getchar();
    for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
    for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
    return sum * fh;
}
void add_Edge(int x, int y) { ++cnt_Edge; Edge[cnt_Edge] = (node){ y, Head[x] }; Head[x] = cnt_Edge; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }

void dfs(int now, int father)
{
    dfn[now] = Low[now] = ++cnt_node; int val = 0;
    for (int i = Head[now]; i; i = Edge[i].Next)
    {
        int u = Edge[i].to;
        if (!dfn[u])
        {
            dfs(u, now); ++val;
            Low[now] = Min(Low[now], Low[u]);
            if (Low[u] >= dfn[now] && now != father) book[now] = 1;
        }
        Low[now] = Min(Low[now], dfn[u]);
    }
    if (now == father && val >= 2) book[now] = 1;
}

int main()
{
    n = read(), m = read();
    for (int i = 1; i <= m; ++i)
    {
        int x = read(), y = read();
        add_Edge(x, y); add_Edge(y, x);
    }
    for (int i = 1; i <= n; ++i)
        if (!dfn[i]) dfs(i, i);
    int ans = 0;
    for (int i = 1; i <= n; ++i)
        if (book[i]) ++ans;
    printf("%d\n", ans);
    for (int i = 1; i <= n; ++i)
        if (book[i]) printf("%d ", i);
    printf("\n"); return 0;
}

3. Bridge

The author has not found the template question yet.

2.1 definitions

The definition of bridge is very similar to that of cut point.

Definition of bridge: for one edge ( u , v ) (u,v) (u,v), if the number of connected blocks of the graph increases after deleting this edge, then this edge is a cut edge, also known as a bridge.

For example, the following picture, ( 4 , 5 ) (4,5) (4,5) this is the bridge in this picture.

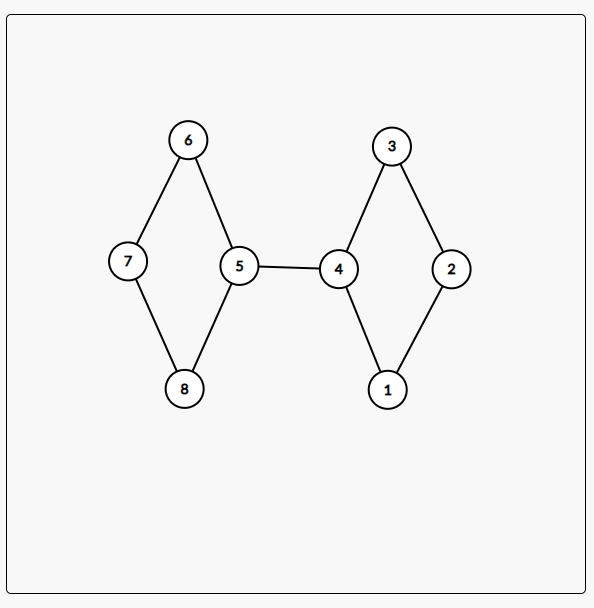
Similarly, a picture may have multiple bridges.

Calculation method

Tarjan algorithm is also adopted, which still needs to be maintained d f n , l o w dfn,low dfn,low.

But this is the opposite side n o w − > u now->u now − > u, if l o w u ≥ d f n n o w low_u \geq dfn_{now} Low ≥ dfnnow, indicating that this edge is a cutting edge.

In particular, we must not follow the original edge when updating, that is, we cannot update from this edge, otherwise the answer will be wrong at this time.

Why?

Because the bridge is essentially the edge between the cut point and a whole connected block, if it is updated l o w low low, there will be such a situation:

If the back edge can be updated, then:

in limine d f n 1 = l o w 1 = 1 dfn_1=low_1=1 dfn1​=low1​=1.

Because the back edge can be updated, then l o w 2 = 1 low_2=1 low2​=1.

It will be satisfied at this time l o w 2 ≥ d f n 1 low_2 \geq dfn_1 low2​≥dfn1​， ( 1 , 2 ) (1,2) (1 and 2) are bridges.

Similarly, l o w 3 = 1 low_3=1 low3​=1.

here l o w 3 < d f n 2 = 2 low_3 < dfn_2=2 low3 < dfn2 = 2, the algorithm judges that it is not a bridge, but it is actually a bridge.

So the algorithm is wrong.

But if the back side can't be updated, there won't be this problem~

code:

/*
========= Plozia =========
    Author:Plozia
    Problem:((no problem at present) [template] Bridge
    Date:2021/5/10
    Remarks:The data range of this question adopts the data range of P3388
========= Plozia =========
*/

#include <bits/stdc++.h>

typedef long long LL;
const int MAXN = 2e4 + 10, MAXM = 1e5 + 10;
int n, m, Head[MAXN], cnt_Edge = 1, Cut[MAXM << 1], Dfn[MAXN], Low[MAXN], cnt_node;
struct node { int to, Next; } Edge[MAXM << 1];

int read()
{
    int sum = 0, fh = 1; char ch = getchar();
    for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
    for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
    return sum * fh;
}
void add_Edge(int x, int y) { ++cnt_Edge; Edge[cnt_Edge] = (node){y, Head[x]}; Head[x] = cnt_Edge; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }

void dfs(int now, int E)
{
    Dfn[now] = Low[now] = cnt_node;
    for (int i = Head[now]; i; i = Edge[i].Next)
    {
        int u = Edge[i].to;
        if (!Dfn[u])
        {
            dfs(u, i);
            Low[now] = Min(Low[now], Low[u]);
            if (Low[u] >= Dfn[now]) Cut[i] = Cut[i ^ 1] = 1;
        }
        else if (i != (E ^ 1)) Low[now] = Min(Low[now], Dfn[u]);
    }
}

int main()
{
    n = read(), m = read();
    for (int i = 1; i <= m; ++i)
    {
        int x = read(), y = read();
        add_Edge(x, y); add_Edge(y, x);
    }
    for (int i = 1; i <= n; ++i)
        if (!Dfn[i]) dfs(i, 0);
    int ans = 0;
    for (int i = 2; i <= cnt_Edge; i += 2)
        if (Cut[i]) ++ans;
    printf("%d\n", ans);
    for (int i = 2; i <= cnt_Edge; i += 2)
        if (Cut[i]) printf("%d %d\n", Edge[i ^ 1].to, Edge[i].to);
    return 0;
}

2.3 error prone points

Here are two common mistakes:

• The connecting edge of two cutting points must be cutting edge.
• The two ends of the cutting edge must be cutting points.

Both of them are actually wrong. The counterexample is as follows:

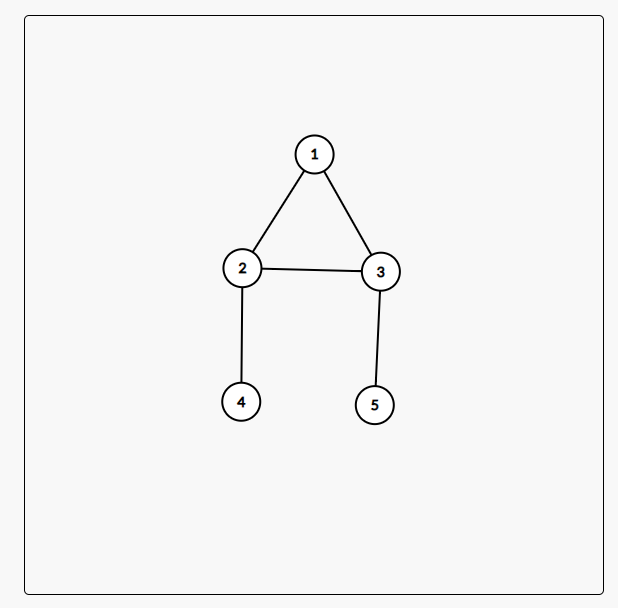
In the above figure, 2 and 3 are cut points, but ( 2 , 3 ) (2,3) (2,3) not edge cutting.

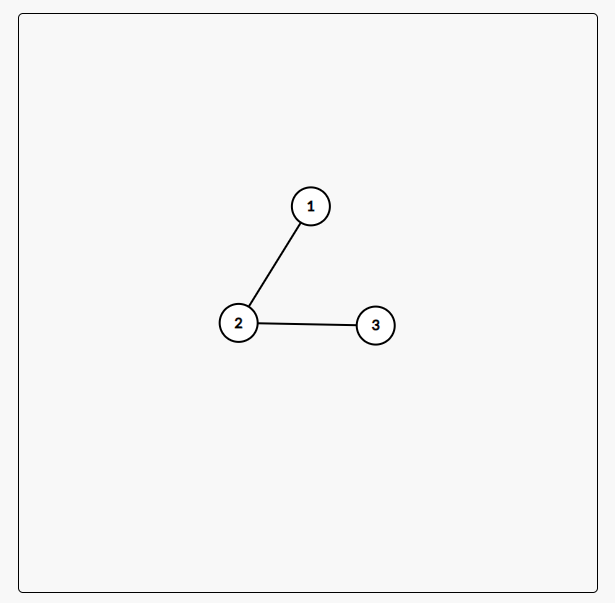
obviously ( 2 , 3 ) (2,3) (2,3) is a cutting edge, but 3 is not a cutting point.

4. Summary

The cutting point and edge algorithm is solved by Tarjan algorithm.

d f n dfn dfn is the timestamp, l o w low low is the minimum timestamp of the earliest point that can be returned (without passing through the parent node).

Remind again: it should not be confused with the Tarjan algorithm for finding strongly connected components!