Directions for the first three phases:
This should be the last issue of backtracking. The previous topics are more conventional, basically what subset or arrangement of written language. This issue summarizes some topics that prefer application. Of course, the essence is still that set.
Examples
Letter combination of telephone numbers
Given a string containing only numbers 2-9, return all letter combinations that can be represented. The mapping relationship between the number and the letter is as follows (that is, our mobile phone keyboard):

Define a mapping vector to facilitate operation
vector<string> mapping{"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};For example, the mapping letter of the number 2 is mapping[2-2][i], and I is the index of the string.
① Select instance "23" to draw
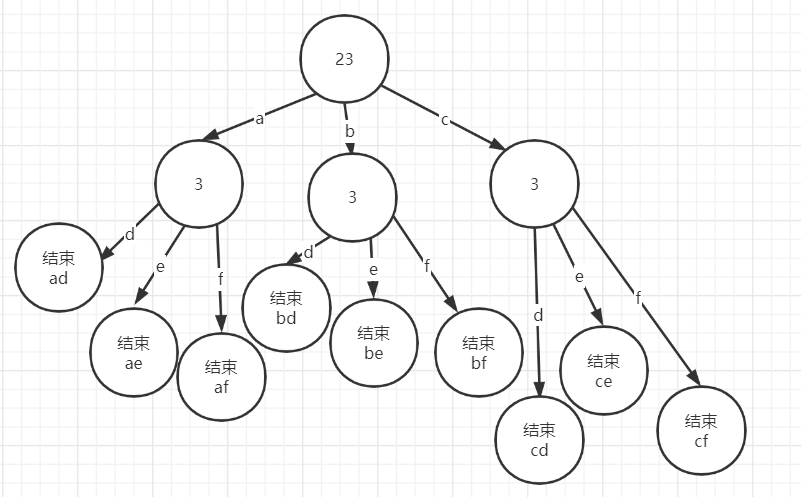
② Determine end condition
Because it is a mapping, the length of the final mapping result is equal to the given character length
//End condition
if(path.length()==digits.length()){
res.push_back(path);
return;
}③ Confirm the selection list. The selection list is the string of digital mapping to be mapped for the current node.
for(int i=0;i<mapping[digits[index]-'0'-2].length();i++)
④ Pruning. It is found that there is no repetition in this drawing. There is no need to prune
⑤ ⑥ ⑦ selection, recursion and cancellation
Since each recursion recurses deep, the character to be mapped is the next one, so index+1
//choice path.push_back(mapping[digits[index]-'0'-2][i]); //recursion dfs(digits,path,res,index+1); //revoke path.pop_back();
Full code:
class Solution {
public:
vector<string> mapping{"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> letterCombinations(string digits) {
string path;
vector<string> res;
if(digits==""){
return res;
}
dfs(digits,path,res,0);
return res;
}
void dfs(string digits, string& path, vector<string>& res, int index){
//End condition
if(path.length()==digits.length()){
res.push_back(path);
return;
}
for(int i=0;i<mapping[digits[index]-'0'-2].length();i++){
//choice
path.push_back(mapping[digits[index]-'0'-2][i]);
//recursion
dfs(digits,path,res,index+1);
//revoke
path.pop_back();
}
}
};bracket-generating
Given a number n to represent the logarithm of generated parentheses, generate all possible and valid parenthesis combinations.
① Select instance n=2 to draw
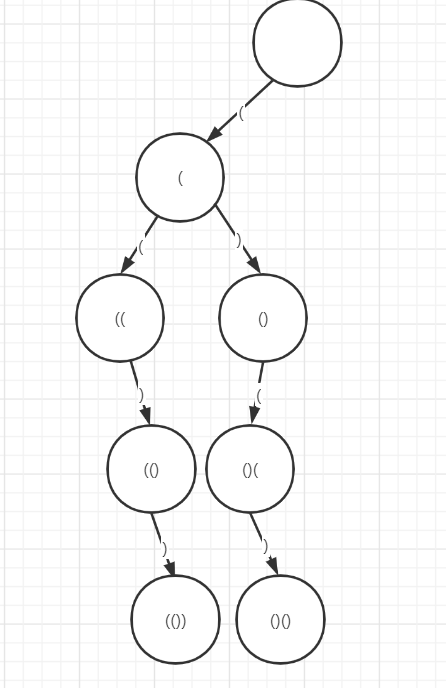
② determine the end conditions
When the number of left parentheses and right parentheses selected is equal to n, it means completion
//End condition
if(left_count==n && right_count==n){
res.push_back(path);
return;
}③ Determine the selection list. The selection list is not so regular. It is related to the selected items of the current node. For example, if the left parentheses of the current node are not selected completely, you can select the left parentheses. If the number of right parentheses is less than the left parentheses, you can select the right parentheses. That is to say, in fact, there is no need to use the for loop for the selection list of this problem. You can use two conditions
//If there are left parentheses, select the left parenthesis if(left_count<n)
//The number of right parentheses is less than the number of left parentheses if(right_count<n && right_count<left_count)
④ Pruning, no pruning
⑤ ⑥ ⑦ selection, recursion and cancellation
//Select the left parenthesis
++left_count;
path.push_back('(');
//recursion
dfs(n,res,path,left_count,right_count);
//revoke
--left_count;
path.pop_back();//Select the closing bracket
++right_count;
path.push_back(')');
//recursion
dfs(n,res,path,left_count,right_count);
//revoke
--right_count;
path.pop_back();Full code:
class Solution {
public:
vector<string> generateParenthesis(int n) {
vector<string> res;
string path;
//Number of left parentheses, number of right parentheses
int left_count,right_count;
dfs(n,res,path,left_count,right_count);
return res;
}
void dfs(int n, vector<string>& res, string& path, int left_count, int right_count){
//End condition
if(left_count==n && right_count==n){
res.push_back(path);
return;
}
//If there are left parentheses, select the left parenthesis
if(left_count<n){
//choice
++left_count;
path.push_back('(');
//recursion
dfs(n,res,path,left_count,right_count);
//revoke
--left_count;
path.pop_back();
}
//The number of right parentheses is less than the number of left parentheses
if(right_count<n && right_count<left_count){
//choice
++right_count;
path.push_back(')');
//recursion
dfs(n,res,path,left_count,right_count);
//revoke
--right_count;
path.pop_back();
}
}
};Word search
Given a two-dimensional array and a string word, judge whether the string exists in the two-dimensional grid. Words must be formed alphabetically by letters in adjacent cells (horizontal or vertical).
① Choose an example to draw, because it's not easy to draw a tree. Instead, the question is very similar DFS question brushing summary Topics in.
Because it is also a two-dimensional lattice, the upper, lower, left and right sides are also used as adjacent nodes.
② Determine end condition
The result is equal to the word
//End condition
if(path==word){
flag=true;
return;
}③ Determine the selection list. The selection list is obviously up, down, left, right and around, but it is not out of bounds and has not been accessed in the current depth traversal. direction is convenient to take four weeks. You can see the issue of dfs summary.
for(int i=0;i<4;i++){
x=l+direction[i];
y=r+direction[i+1];
if(x>=0 && x<board.size() && y>=0 && y<board[0].size() && !visited[x][y]){
}
}④ Pruning is not equal to the pruning of the current word characters, that is, only the ones that match are selected
if(board[x][y]!=word[start]){
continue;
}Non conforming skip can be written as conforming before selection
if(board[x][y]==word[start]){
//choice
}⑤ ⑥ ⑦ selection, recursion and cancellation
Since one character of the word is matched each time, the next recursive selection is to match the next character, so it is start+1.
//choice path.push_back(word[start]); visited[x][y]=true; //recursion dfs(board,word,path,flag,x,y,visited,start+1); //revoke path.pop_back(); visited[x][y]=false;
Full code:
class Solution {
public:
vector<int> direction{-1,0,1,0,-1};
bool exist(vector<vector<char>>& board, string word) {
string path;
bool flag=false;
int m=board.size(),n=board[0].size();
vector<vector<bool>> visited(m,vector<bool>(n,false));
for(int i=0;i<m;i++){
if(flag) break;
for(int j=0;j<n;j++){
if(flag) break;
if(board[i][j]==word[0]){
//choice
path.push_back(word[0]);
visited[i][j]=true;
dfs(board,word,path,flag,i,j,visited,1);
//revoke
path.pop_back();
visited[i][j]=false;
}
}
}
return flag;
}
//The of this flag & don't forget to add it
void dfs(vector<vector<char>>& board, string word, string& path, bool& flag,int l,int r,vector<vector<bool>>& visited,int start){
//End condition
if(path==word){
flag=true;
return;
}
int x,y;
for(int i=0;i<4;i++){
x=l+direction[i];
y=r+direction[i+1];
if(x>=0 && x<board.size() && y>=0 && y<board[0].size() && !visited[x][y]){
if(board[x][y]==word[start]){
//choice
path.push_back(word[start]);
visited[x][y]=true;
//recursion
dfs(board,word,path,flag,x,y,visited,start+1);
//revoke
path.pop_back();
visited[x][y]=false;
}
}
}
}
};