preface
hello, everyone, I'm bigsai brother. I haven't seen you for a long time. I miss you very much 🤩!
Today, I'll share a TOPK problem, but I don't consider a particularly large distributed solution here. It's an ordinary algorithm problem.
First, find out what is the topK problem?
The topK problem is to find out the number of the first k in the sequence. The idea of solving the topK problem is roughly the same as that of the first k (or small).
TOPK question is a very classic question. It appears very, very frequently in written examination and interview (never telling lies). Next, from Xiaobai's starting point, I think TOPK is a big problem for the top K. let's get to know TOPK together!
At present, the solution of TOPK is almost the same as that of the k-th problem. Here, we will buckle the k-th element of 215 array as the solution. Before learning TOPK, this article Top ten orders that programmers must know and know Be sure to.
Sorting method
Find TopK and sort TopK
What, you want me to find TopK? Not only TopK, how many do you want, how many do I give you, and sort them for you. What sort am I most familiar with?
If you think of bubble sort O(n^2), you're careless.
If you use the O(n^2) level sorting algorithm, it also needs to be optimized. Bubble sorting and simple selection sorting can determine a maximum (minimum) value in order each time, so you don't need to sort all the data. You only need to execute it K times, so the time complexity of this algorithm is also O(nk).
Here, let's review the difference between bubble sorting and simple selection sorting:
Bubble sorting and simple selection sorting are multiple times. Each time, a maximum or minimum can be determined. The difference is that bubble is only compared with its own back in the enumeration process. If it is larger than the back, it will be exchanged; The simple choice is to mark a maximum or minimum number and position each time, and then exchange it with the last position number of this trip (determine a number in each trip, and the enumeration range gradually decreases).
The process is shown in a diagram below:
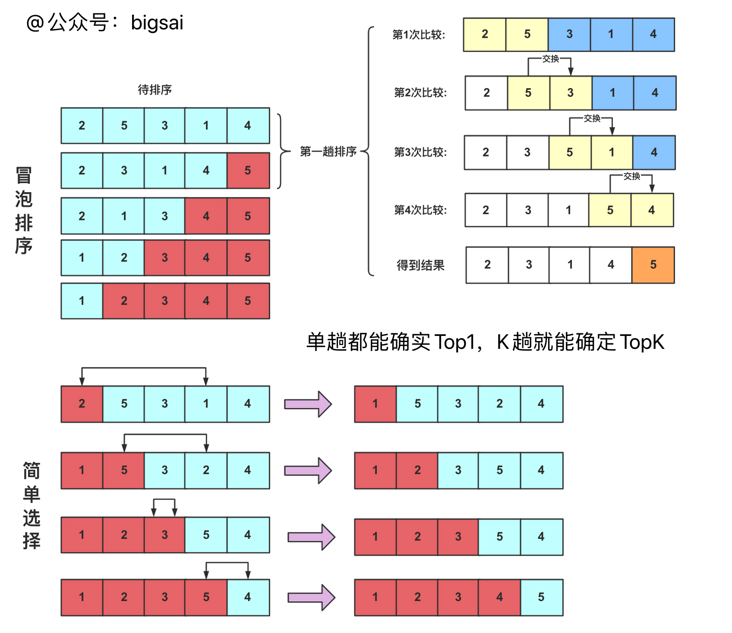
Here, the code is also provided for you. A simple choice is shown in the figure above. You can choose the minimum every time. When you implement it, you can choose the maximum every time.
//Swap two position elements in an array
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
//Bubble sorting implementation
public int findKthLargest1(int[] nums, int k) {
for(int i=nums.length-1;i>=nums.length-k;i--)//It's only k times here
{
for(int j=0;j<i;j++)
{
if(nums[j]>nums[j+1])//Compare with the neighbor on the right
{
swap(nums,j,j+1);
}
}
}
return nums[nums.length-k];
}
//Simple choice implementation
public int findKthLargest2(int[] nums, int k) {
for (int i = 0; i < k; i++) {//It only takes K times
int max = i; // Minimum position
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] > nums[max]) {
max = j; // Replace the minimum position
}
}
if (max != i) {
swap(nums, i, max); // Exchange with position i
}
}
return nums[k-1];
}Of course, fast sorting, merge sorting and even heap sorting are OK. The time complexity of these sorting is O(nlogn), that is, sort all data and directly return the results. This part will not be explained in detail. You can adjust api or handwritten sorting.
For the two ideas, O(nk) is faster except for the case of K minimum. In fact, O(nlogn) is faster in most cases. However, it is rewarding to think of O(nk) from O(n^2).
Heap based optimization
Here you need to know about heap. I have written about priority queue and heap sorting before. I won't repeat it here. You can also take a look at it:
I don't know the priority queue. Let's look at the heap sort
As mentioned above, heap sorting O(nlogn) is to sort all elements and then take the first k, but in fact, let's analyze the process of heap sorting and several points for attention:
Heap data structure is divided into large root heap and small root heap. The small root heap is that the value of the parent node is less than the value of the child node, and the large root heap is that the value of the parent node is greater than the value of the child node. Here, the large root heap must be used.
The heap looks like a tree structure, but the heap is a complete binary tree. We use the array storage efficiency is very high, and it is also very easy to use the subscript to directly find the parent and child nodes, so we use the array to realize the heap. Each time the sorted node moves the number to the end of the array, so that a new array forms a new heap to continue.
From a large point of view, heap sorting can be divided into two parts: building a heap with an unordered array and sorting at the top of the heap each time. The time complexity of building a heap for an unordered array is O(n). Sort on the basis of the heap, take the top element each time, and then move the last element to the top of the heap to adjust the heap. Each time, only the time complexity of O(logn) level is required. O(nlogn) is required to complete sorting n times, but we only need K times each time, so it takes O(klogn) time complexity to complete the sorting function of k elements, The whole time complexity is O(n+klogn), because it is not merged after distinguishing from the previous one.
Draw a picture to help you understand. You can get Top2 after two times and TopK after k times.
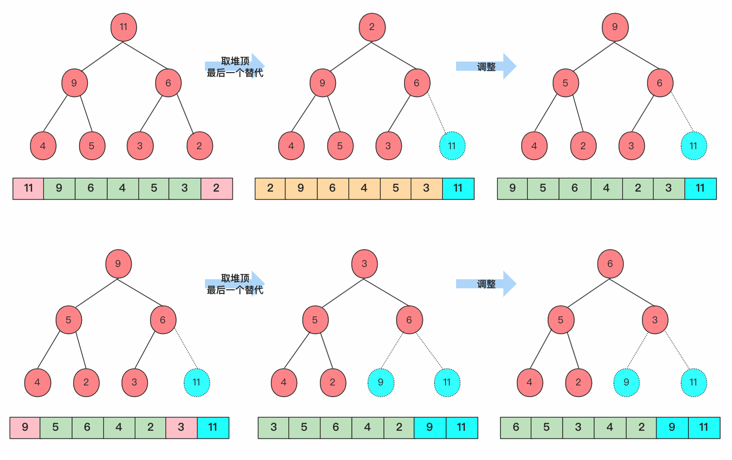
The implementation code is:
class Solution {
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
//Move down switching effectively transforms the current node into a heap (large root)
public void shiftDown(int arr[],int index,int len)//Position 0 is not used
{
int leftchild=index*2+1;//Left child
int rightchild=index*2+2;//Right child
if(leftchild>=len)
return;
else if(rightchild<len&&arr[rightchild]>arr[index]&&arr[rightchild]>arr[leftchild])//The right child is in range and should be exchanged
{
swap(arr, index, rightchild);//Exchange node value
shiftDown(arr, rightchild, len);//It may affect the heap of child nodes. Refactor down
}
else if(arr[leftchild]>arr[index])//Exchange left child
{
swap(arr, index, leftchild);
shiftDown(arr, leftchild, len);
}
}
//Create arrays into piles
public void creatHeap(int arr[])
{
for(int i=arr.length/2;i>=0;i--)
{
shiftDown(arr, i,arr.length);
}
}
public int findKthLargest(int nums[],int k)
{
//Step 1 reactor building
creatHeap(nums);
//Step 2 takes values k times to build a heap, and each time takes the top element of the heap and puts it at the end
for(int i=0;i<k;i++)
{
int team=nums[0];
nums[0]=nums[nums.length-1-i];//Delete the top element and put the end element at the top of the heap
nums[nums.length-1-i]=team;
shiftDown(nums, 0, nums.length-i-1);//Adjust this heap to a legal large root heap. Note that the (logical) length changes
}
return nums[nums.length-k];
}
}Based on fast scheduling optimization
The above heap sorting can be optimized. What about fast sorting?
Of course I can. How can I do less than I do?
This part requires a certain understanding and understanding of fast stacking. It was written a long time ago: Illustration: hand tearing, bubbling and quick row (to be optimized later), the core idea of fast scheduling is: divide and conquer, determine the position of a number each time, and then divide the number into two parts. The left side is smaller than it and the right side is larger than it, and then call this process recursively. The time complexity of each adjustment is O(n), and the average number of times is log n times, so the average time complexity is O (n logn).
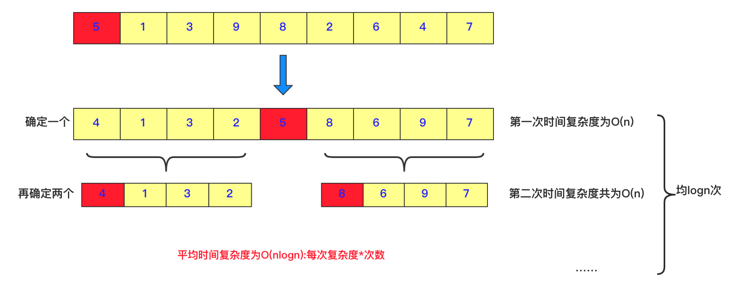
But what does this have to do with seeking TopK?
When we seek TopK, we actually seek K numbers larger than the target number. We randomly choose a number. For example, there are 4 numbers on the left and 4 numbers on the right of 5 and 5 above. The following situations may occur:
① If k-1 is equal to the number on the right side of 5, then the middle 5 is the K, and it and its right side are TopK.
② If k-1 is less than the number on the right side of 5, it means that the TopK is all on the right side of 5. Then you can directly compress the space to the right side and continue to call the same method recursively.
③ If k-1 is greater than the number on the right side of 5, it means that the right side and 5 are all in TopK, and then there are on the left side (k - including the total number on the right side of 5). At this time, the search range is compressed and K is also compressed. For example, if k=7, the right side of 5 and 5 already accounts for 5 numbers, which must be in top 7. We only need to find top 2 on the left side of 5.
In this way, each value will be compressed. Here, because the fast scheduling is not completely recursive, and the time complexity is not O(nlogn) but O(n) level (for details, you can find some online proofs), but some extreme codes in the test samples, such as 1 2 3 4 5 6... When you find Top1, there are more extreme situations. Therefore, a random number will be used to exchange with the first one to prevent special examples (just for brushing questions). Of course, I don't add random exchange here, and if the TopK to be obtained here is not sorted.
The detailed logic can be seen in the following implementation code:
class Solution {
public int findKthLargest(int[] nums, int k) {
quickSort(nums,0,nums.length-1,k);
return nums[nums.length-k];
}
private void quickSort(int[] nums,int start,int end,int k) {
if(start>end)
return;
int left=start;
int right=end;
int number=nums[start];
while (left<right){
while (number<=nums[right]&&left<right){
right--;
}
nums[left]=nums[right];
while (number>=nums[left]&&left<right){
left++;
}
nums[right]=nums[left];
}
nums[left]=number;
int num=end-left+1;
if(num==k)//Terminate when k is found
return;
if(num>k){
quickSort(nums,left+1,end,k);
}else {
quickSort(nums,start,left-1,k-num);
}
}
}Counting and sorting
Sorting always has some operations - linear sorting, so you may ask if bucket sorting is OK?
It's OK, but it depends on the numerical range for optimization. Bucket sorting is suitable for the case of uniform and dense data with a large number of occurrences, and counting sorting hopes that the numerical value can be smaller.
So what is the specific core idea of using bucket sorting?
First, count and sort the number of occurrences of each number, and then stack and sum a new array from back to front.
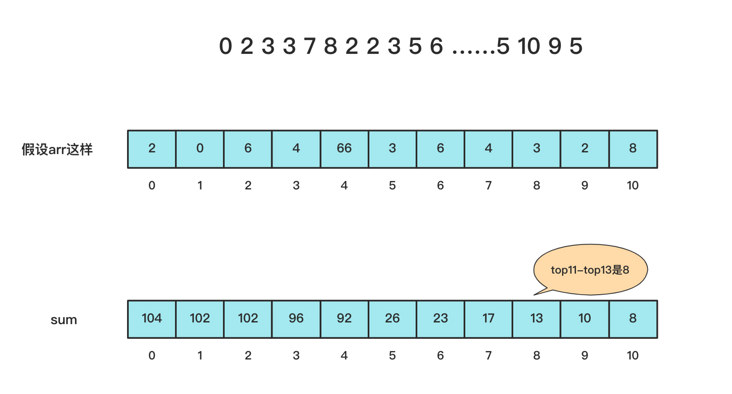
This situation is very suitable for the case of large numerical value and small distribution range.
I didn't want to write the code, but you will write it for me for three times
//Force buckle 215
//1 <= k <= nums.length <= 104
//-104 <= nums[i] <= 104
public int findKthLargest(int nums[],int k)
{
int arr[]=new int[20001];
int sum[]=new int[20001];
for(int num:nums){
arr[num+10000]++;
}
for(int i=20000-1;i>=0;i--){
sum[i]+=sum[i+1]+arr[i];
if(sum[i]>=k)
return i-10000;
}
return 0;
}epilogue
Well, that's all for today's TopK problem. I'm sure you'll handle it next time.
The TopK problem is not difficult. It's just a clever use of sorting. Ranking is very important. Interviews will be very high frequency.
Here, I won't hide a showdown. How can I guide you to talk about TOPK from the perspective of the interviewer.
Cunning Interviewer:
Well, let's talk about data structures and algorithms. Let's talk about sorting. You should have been in touch with it? Tell the three sorting methods you are most familiar with, and explain the specific algorithm.
Humble me:
bia la bia la bia la bia la......
If you mention fast sorting and bucket sorting, you may use this sorting to realize the TopK problem, and other sorting may also be possible, so it is very necessary to master the top ten sorting!
First official account: bigsai, please attach the link here. It's not easy to create. Thank you for your attention.