Original address: http://moilk.org/blog/2016/10/27/ccf2016094/
Problem description
After visiting China, King G was deeply shocked by China's high-speed railway and decided to build a high-speed railway system for his country.
In order to save construction costs, King G decided not to build new railways, but to transform existing railways into high-speed railways. Now, please provide King G with a plan to transform some of the existing railways into high-speed railways, so that any two cities can reach by high-speed railways, and the shortest distance from all cities to the capital by high-speed railways is as long as before. Please tell King G how long the railways will be altered at least under these conditions.
Input Format
The first line of input contains two integers n and m, representing the number of cities in G and the number of inter-city railways, respectively. All cities are numbered from 1 to N and the capital is No. 1.
The next m lines, each with three integers a, b, c, indicate that there is a two-way railway with a length of C between city a and city B. This railway will not pass through cities other than A and B.
Output format
The output line represents the minimum length of the railway to be reformed if the conditions are met.
Sample input
4 5
1 2 4
1 3 5
2 3 2
2 4 3
3 4 2
Sample output
11
Evaluate the size and conventions of use cases
For 20% of the evaluation cases, 1 < n < 10, 1 < m < 50;
For 50% of the test cases, 1 < n < 100, 1 < m < 5000;
For 80% of the test cases, 1 < n < 1000, 1 < m < 50000;
For 100% of the evaluation cases, 1 < n < 10000, 1 < m < 100000, 1 < a, b < n, 1 < c < 1000. Input ensures that every city can reach the capital by rail.
Solution Notes
First, look at the title, "The shortest distance from all cities to the capital by high-speed railway is as long as the original one", which shows that the result satisfies the single-source shortest path; and "How many railways should be reformed at least", which means that the minimum cost should be found in the shortest path. As shown in the figure below, the shortest path from point 1 to point 3 is 4. To connect point 3, 1-2-3, 1-3 and 1-4-3 are the shortest paths. However, if 1-3 is chosen, the rails need to be increased by 4 units; if 1-2-3 is selected, the rails need to be increased by 2 units; and if 1-4-3 is selected, the rails need to be increased by only 1 unit. So the last option should be chosen at this time.
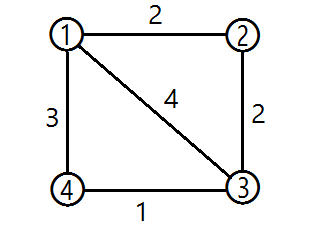
Only dijkstra is needed for program implementation algorithm Just add a little bit of code. We use D algorithm not to get the shortest path, but to get the minimum additional edges of each point connected under the shortest path. If costo[v] is used to denote the weight of the added edges of connected v-points, such as costo[3]=1 in the figure above. When confronted with the above options, that is, disto[v]==disto[u]+cost, let costo[v]=min(costo[v],cost), so that the final costo[v] is the minimum cost to meet the shortest path conditions.
Adjacent tables
#include <iostream> #include <queue> #include <vector> #define NMAX 10005 #define INTMAX 0x7fffffff using namespace std; // v denotes the node and cost denotes the distance from the starting point to v point struct Node { int v; int cost; Node(int vv = 0, int c = 0){ v = vv, cost = c; } // Priority queues will be arranged from small to large distances friend bool operator < (Node n1, Node n2){ return n1.cost > n2.cost; } }; // v denotes the node at the other end of the edge, and cost denotes the weight of the edge. struct Edge { int v; int cost; Edge(int vv = 0, int c = 0){ v = vv, cost = c; } }; vector<Edge>G[NMAX];// Undirected graph bool marked[NMAX];// Each vertex is processed only once in D algorithm int disto[NMAX];// The distance from the starting point to a certain point int costo[NMAX];// Weight of additional edges needed to connect this point int N, M; void dijkstra(int s){ for(int i = 0 ; i <= N ; i++){ costo[i] = disto[i] = INTMAX; marked[i] = false; } disto[s] = 0; costo[s] = 0; priority_queue<Node>pq;// Preserve < v, disto[v] > and arrange in ascending order of disto[v]. pq.push(Node(s, 0)); marked[0] = true; Node tmp; while(!pq.empty()){ tmp = pq.top(); pq.pop(); int v = tmp.v; if(!marked[v]){ marked[v] = true; int len = G[v].size(); for(int i = 0 ; i < len ; i++){ int vv = G[v][i].v; if(marked[vv]) continue; int cost = G[v][i].cost; int newdist = disto[v] + cost; if(disto[vv] > newdist){ disto[vv] = newdist; costo[vv] = cost;// Additional content pq.push(Node(vv, disto[vv])); } // Additional content // If there are many schemes with the same distance when adding point vv, choose the smallest one of the new edges. if(disto[vv] == newdist){ costo[vv] = min(costo[vv], cost); } } } } } int main(void){ cin >> N >> M; int s, e, c; for(int i = 0 ; i < M ; i++){ cin >> s >> e >> c; G[s].push_back(Edge(e, c)); G[e].push_back(Edge(s, c)); } dijkstra(1); // Statistical Edge Weight int res = 0; for(int i = 2 ; i <= N ; i++){ res += costo[i]; } cout << res << endl; return 0; }
Adjacency matrix, supermemory
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #define LL long long int const MAX = 1111; int const INF = 1 << 30; using namespace std; int g[MAX][MAX]; bool vis[MAX]; int n, m; //d[i] is the smallest distance to the node, and cost[i] is the additional cost to extend to the node. int d[MAX], cost[MAX]; void dijk(int st){ //Setting the initial paper infinity fill(d, d + MAX, INF); d[st] = 0; cost[st] = 0; for(int i = 1 ; i <= n ; i++){ int u = -1, mind = INF; for(int j = 1 ; j <= n ; j++) if(vis[j] == 0 && d[j] < mind){ u = j; mind = d[j]; } if(u == -1) return; vis[u] = 1; for(int v = 1 ; v <= n ; v++){ int t = d[u] + g[u][v]; if(vis[v] == 0 && g[u][v] != INF && t < d[v]){ d[v] = t; cost[v] = g[u][v]; } else if(vis[v] == 0 && g[u][v] != INF && t == d[v]){ cost[v] = min(cost[v], g[u][v]); } } } } int main(int argc, char*argv[]){ scanf("%d %d", &n, &m); fill(g[0], g[0] + MAX * MAX, INF); while(m--){ int x, y, z; scanf("%d %d %d", &x, &y, &z); g[x][y] = g[y][x] = z; } dijk(1); int ans = 0; for(int i = 2 ; i <= n ; i++) ans += cost[i]; printf("%d\n", ans); return 0; }