Travel
Time limit: up to X use cases, 2 seconds (C/C + +), 2.5 seconds (Java)
There is currently a country with an N-row M-column grid model. Each cell represents a city. Every time you pass through a city, a toll will be generated.
A grand celebration will be held in a city in this country this summer. In order to participate in the celebration, John and Chloe need to start from their own city to the city hosting the celebration. When you go, you can move to the adjacent cities up, down, left and right. Once you leave a city, you need to pay the toll immediately. In addition, because the toll is charged by group rather than by number of people, it costs less to meet in a city on the way and travel together than travel alone.
 < Figure 1 > < Figure 2 >
< Figure 1 > < Figure 2 >
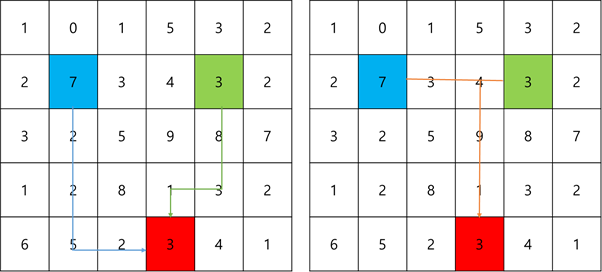
As shown in the above figure, suppose John lives in [2,2], Chloe lives in [2,5], and the city hosting the celebration is located in [5,4]. (at this time, the first number in the coordinates represents the number of rows, the second number represents the number of columns, and the number in each cell represents the toll.) The lowest cost path for John to the celebration city is the blue path < Figure 1 >, which is 18. In the case of Chloe, the lowest cost path is the green path, which is 15. If John and Chloe meet on [2,4] and move together as shown in < Figure 2 >, the cost will become 10 + 3 + (4 + 9 + 1) = 27, and the cost is the lowest.
※ cities holding celebrations do not charge tolls; The city John and Chloe pass through together can pay the toll together.
Help John and Chloe find out the minimum cost when they move to the city where the celebration is held.
[restrictions]
1. The number of rows N and columns m of the grid are integers between 3 and 500. (3 <= N, M <= 500)
2. The toll C of each city is an integer between 0 and 10000. (0 <= C <= 10,000)
3. Even if you pass through a city you have been to, you still need to pay the toll again.
4. If two people travel together, only one toll will be charged.
5. Cities holding celebrations do not charge tolls. If they meet in the departure city and travel together, they will charge a toll, but only pay one person.
6. The city where John lives, the city where Chloe lives and the city where celebrations are held are three different cities.
[input]
The first line gives the number of test cases T, and then gives t test cases. The first row space distinguishes the row number N and column number m of the given grid, the row number R1 and column number C1 of John's departure city, the row number R2 and column number C2 of krui's departure city, and the row number R3 and column number C3 of celebration activities. Next, the tolls (C) of M cities are given through N lines and spaces in each line.
[output]
A test case outputs one line. Each test case outputs "#x" (where X represents the test case number, starting from 1). After adding a space, the minimum cost required for John and Chloe to go to the city hosting the celebration is output.
[input / output example]
(input)
3
5 6 2 2 2 5 5 4
1 0 1 5 3 2
2 7 3 4 3 2
3 2 5 9 8 7
1 2 8 1 3 2
6 5 2 3 4 1
6 9 1 9 6 1 4 6
7 7 5 2 7 4 7 6 1
6 4 9 4 10 3 4 7 5
10 9 8 4 10 8 3 10 10
8 7 4 8 2 2 2 2 2
1 3 9 6 9 1 6 1 9
6 4 3 10 5 7 8 7 2
5 5 3 3 3 4 3 5
4 5 9 1 8
1 9 3 1 8
2 1 3 5 10
3 6 6 2 7
2 8 8 0 8
(output)
#1 27
#2 53
#3 8
Train of thought analysis:
The problem can be summarized as follows: point A, point B meet at point D, and then reach point C
Calculate the shortest path from points A, B and C to all points respectively. The shortest path of each point i = A to i+B to i+C to i-2 * the weight of current point i - the weight of point C
Then traverse all points to find the path with the shortest distance
package pro.dijkstra;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
/**
* Train of thought analysis:
* The problem can be summarized as follows: point A, point B meet at point D, and then reach point C
* Calculate the shortest path from points A, B and C to all points respectively. The shortest path of each point i = A to i+B to i+C to i-2 * the weight of current point i - the weight of point C
* Then traverse all points to find the path with the shortest distance
* @author XA-GDD
*
*/
public class Travel_0622 {
static int T,N,M,R1,C1,R2,C2,R3,C3;
static int _max_Nval = 500;
static int _max_Mval = 500;
static int [][] cost = new int[_max_Nval+1][_max_Mval+1];
static int [][][] minCost = new int [_max_Nval+1][_max_Mval+1][4]; //Minimum cost
static int [][] visited = new int[_max_Nval+1][_max_Mval+1];
static int [][] dir = {{-1,0},{0,1},{1,0},{0,-1}}; //direction
static long ANS;
public static void main(String[] args) throws IOException {
System.setIn(new FileInputStream("D:\\workspace\\eclipse-workspace\\sw_pro\\test_case\\sample_input_0622.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
T = Integer.parseInt(st.nextToken());
for(int testCase=1;testCase<=T;testCase++) {
init();
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
R1 = Integer.parseInt(st.nextToken());
C1 = Integer.parseInt(st.nextToken());
R2 = Integer.parseInt(st.nextToken());
C2 = Integer.parseInt(st.nextToken());
R3 = Integer.parseInt(st.nextToken());
C3 = Integer.parseInt(st.nextToken());
init();
for(int i=1;i<=N;i++) {
st = new StringTokenizer(br.readLine());
for(int j=1;j<=M;j++) {
cost[i][j] = Integer.parseInt(st.nextToken());
}
}
dijkstra(new int[] {R1,C1},1); //Shortest distance from (R1,C1) point to all points
dijkstra(new int[] {R2,C2},2); //(R2,C2) shortest distance from point to all points
dijkstra(new int[] {R3,C3},3); //(R3,C3) shortest distance from point to all points
for(int i=1;i<=N;i++) {
for(int j=1;j<=M;j++) {
ANS = Math.min(ANS, minCost[i][j][1]+minCost[i][j][2]+minCost[i][j][3]-2*cost[i][j]-cost[R3][C3]);
}
}
System.out.println("#"+testCase+" "+ANS);
}
}
static void init() {
ANS=Long.MAX_VALUE;
for(int i=0;i<cost.length;i++) {
Arrays.fill(cost[i], 0);
Arrays.fill(visited[i], 0);
}
for(int i=1;i<=N;i++) {
for(int j=1;j<=M;j++) {
Arrays.fill(minCost[i][j], Integer.MAX_VALUE>>1);
}
}
}
static void dijkstra(int [] start, int bound) {
PriorityQueue<int []> pq = new PriorityQueue<int[]>(new Comparator<int []>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2]-o2[2];
}
});
//Each call needs to be initialized, otherwise the second point and the third point will not be traversed when seeking the shortest path
for(int i=0;i<visited.length;i++) {
Arrays.fill(visited[i], 0);
}
minCost[start[0]][start[1]][bound] = cost[start[0]][start[1]];
pq.add(new int [] {start[0],start[1],minCost[start[0]][start[1]][bound]});
while(!pq.isEmpty()) {
int [] curr = pq.poll();
if(visited[curr[0]][curr[1]]==1) {
continue;
}
visited[curr[0]][curr[1]] = 1;
for(int i=0;i<4;i++) {
int x = curr[0] + dir[i][0];
int y = curr[1] + dir[i][1];
if(isValid(x,y)) {
if(minCost[x][y][bound]>minCost[curr[0]][curr[1]][bound]+cost[x][y]) {
minCost[x][y][bound] = minCost[curr[0]][curr[1]][bound]+cost[x][y];
pq.add(new int[] {x,y,minCost[x][y][bound]});
}
}
}
}
}
static boolean isValid(int x,int y) {
return x>0&&x<=N&&y>0&&y<=M;
}
}