Pre knowledge: related terms of graph and representation of graph

Traversal of Graphs

Similar to the tree data structure, we can access all nodes of the graph. The graph can be traversed by two algorithms: breadth first search (BFS) and depth first search (DFS). Graph traversal can be used to find a specific vertex or the path between two vertices, check whether the path is the same, check whether the graph has a ring, and so on.

Before implementing the algorithm, let's better understand the idea of traversal.

The idea of graph traversal algorithm is to track each node visited for the first time, and track which nodes have not been fully explored. For both graph traversal algorithms, it is necessary to clearly point out the first visited vertex.

Fully exploring the first vertex requires us to look at each edge of the vertex. The vertices connected by each edge that have not been accessed are marked as discovered and added to the list of points to be accessed.

In order to ensure the efficiency of the algorithm, each vertex must be visited at most twice. Each edge and vertex in the connected graph is accessed.

Breadth first search algorithm and depth first search algorithm are basically the same, with one difference, that is, the data structure of the vertex list to be accessed. As shown in the following table

algorithm	data structure	describe
Depth first search	Stack	The vertices are stored in the stack. The vertices are explored along the path, and new adjacent vertices are accessed
Breadth first search	queue	The vertices are stored in the queue, and the vertices that enter the queue first are searched first

When we want to label vertices that have been visited, we use three colors to reflect their state.

• White: indicates that the vertex has not been accessed.
• Gray: indicates that the vertex has been visited but not explored.
• Black: indicates that the vertex has been visited and fully explored.

This is why it is important to visit each vertex up to two times as mentioned earlier.

To help mark fixed points in breadth first and depth first algorithms. We will use the Colors variable (as an enumerator) and declare it as follows.

const Colors = {
    WHITE: 0,
    GREY: 1,
    BLACK: 2
};

Both algorithms also need to access a helper object to help store whether vertices have been accessed. At the beginning of each algorithm, all vertices are marked as unreachable (white). We will initialize the color of each vertex with the following function.

const initColor = vertices => {
    const color = {};
    for(let i = 0; i < vertices.length; i++){
        color[vertices[i]] = Colors.WHITE;
    }
    return color
}

Breadth first search

The breadth first search algorithm will traverse the graph from the specified first vertex, and access all its adjacent points (adjacent vertices) first, just like accessing one layer of the graph at a time. In other words, it is the access vertex from width to depth, as shown in the following figure

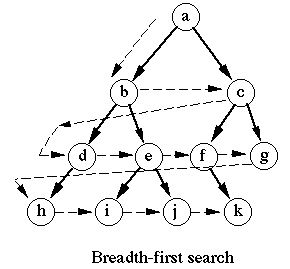
The following are the steps followed by the breadth first search algorithm starting from vertex v.

(1) Create a queue Q.
(2) Mark v as found (gray) and put v into queue Q.
(3) If Q is not empty, run the following steps:
(a) Queue u out of Q;
(b) Marked u as discovered (gray);
© Queue u all unreachable neighbors (white);
(d) Marked u as explored (black).

Let's implement the breadth first search algorithm.

export const breathFirstSearch = (graph, startVertex, callback) => {
    const startVertex = graph.getVertices;
    const adjList = graph.getAdjList;
    const color = initColor(vertices);

    const queue = new Queue();

    queue.enqueue(startVertex);

    while(!queue.isEmpty()){
        const u = queue.dequeue();
        const neighbors = adjList.get(u);
        color[u] = Colors.GREY;
        for(let i = 0; i < neighbors.length; i++){
            const w = neighbors[i];
            if(color[w] === Colors.WHITE){
                color[w] = Colors.GREY;
                queue.enqueue(w);
            }
        }
        color[u] = Colors.BLACK;
        if(callback){
            callback(u);
        }
    }
};

Depth first search element

The depth first search algorithm will traverse the graph from the first specified vertex, follow the path until the last vertex of Lu Jing is accessed, and then go back to the original path and explore the next path. In other words, it accesses vertices in depth and then in breadth, as shown in the following figure

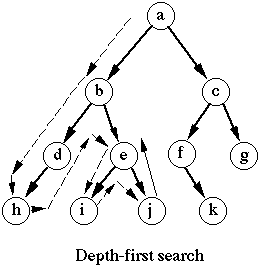
The depth first search algorithm does not require a source vertex. In the depth first search algorithm, if the vertex v in the graph is not accessed, the vertex v is accessed.

To access vertices v, follow these steps:
(1) Marked v as undetected (gray);
(2) For all unreachable (white) adjacent points w of v, access vertex W;
(3) Marked v as explored (black);

The step of depth first search is recursive, which means that the depth first search algorithm uses a stack to store function calls (the stack created by recursive calls).

Let's implement the depth first algorithm.

const depthFirstSearch = (graph, callback) => {
    const startVertex = graph.getVertices();
    const adjList = graph.getAdjList();
    const color = initColor(vertices);

    for(let i = 0; i < neighbors.length; i++){
        if(color[vertices[i]] === Colors.WHITE){
            depthFirstSearchVisit(vertices[i], color, adjList, callback);
        }
    }
};

const depthFirstSearchVisit = (u, color, adjList, callback) => {
    color[u] = Colors.GRAY;
    if(callback){
        callback(u)
    }
    const neighbors = adjList.get(u);
    for(let i = 0; i < neighbors.length; i++){
        const w = neighbors[i];
        if(color[w] === Colors.WHITE){
            depthFirstSearchVisit(w, color, adjList, callback);
        }
    }
    color[u] = Colors.BLACK;
};

The reason for writing this article is that during the interview, the interviewer saw that I wrote the data structure and algorithm (leetcode 120 +) on my resume, so he asked which aspect of the question I was doing, and the answer was array and tree. On the one hand, let's write the first order traversal. This is written. On the other hand, let's change personal questions, breadth first search and depth first search. Ah, I can't answer that. At that time, I saw these two concepts while learning the graph, but the graph is already the last data structure introduced in the book, and it is not very common, so I didn't finish reading that chapter. In addition, I already learned node JS, network accounting, asynchronous and other knowledge with a large amount of information. Later, I was learning to write in the framework, so I didn't study the data structure and algorithm