Binary tree (BST) basic traversal -- depth first

In many cases, we may need to traverse the tree like traversing an array, so as to take out each element stored in the tree. Because the tree structure is different from the linear structure, it cannot traverse backward from the beginning, so there is a problem of how to traverse, that is, according to what search path.

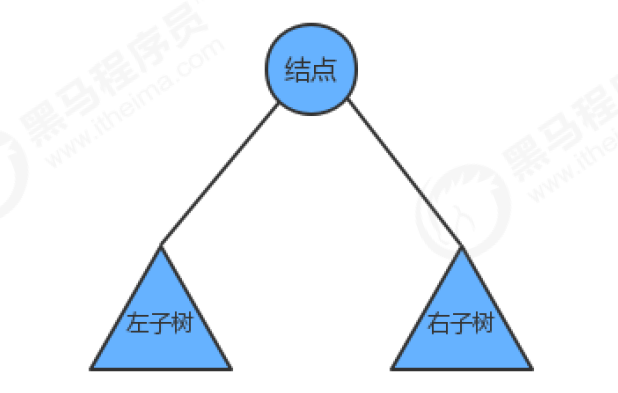
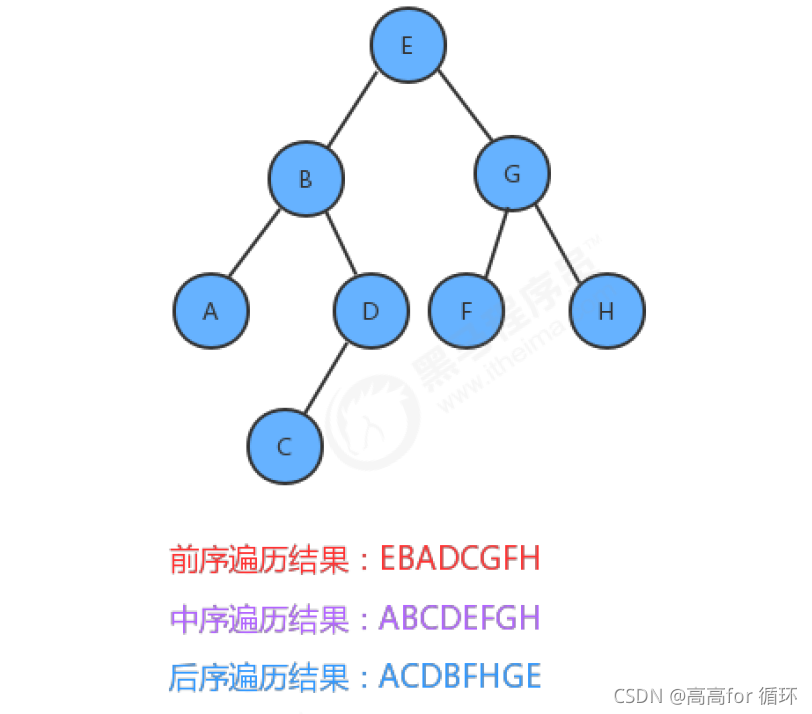
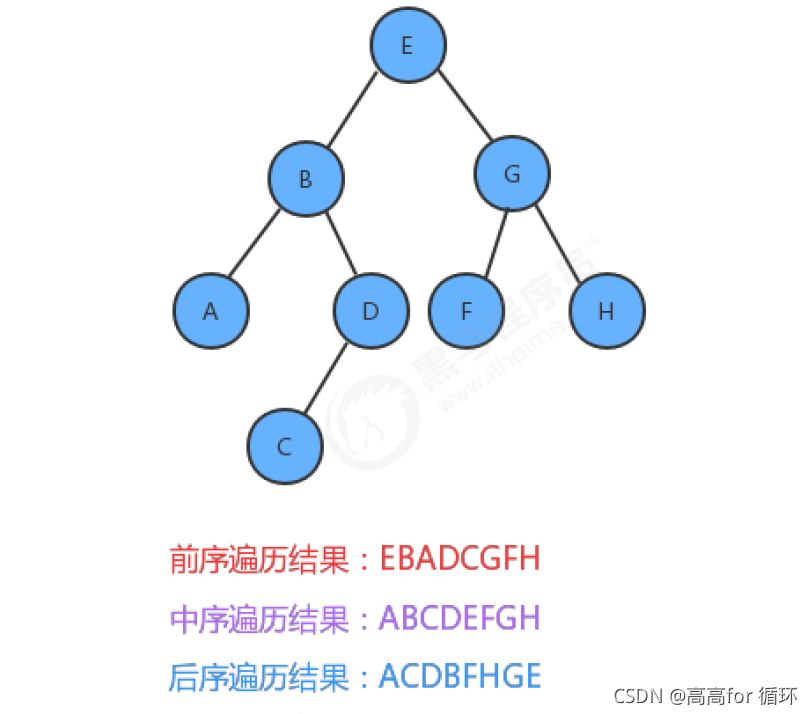
We simply draw the tree as shown in the figure above, which is composed of a root node, a left subtree and a right subtree. According to when the root node is accessed, we can divide the traversal of the binary tree into the following three ways:

1. Preorder traversal;
   Access the root node first, then the left subtree, and finally the right subtree
2. Middle order traversal;
   Access the left subtree first, access the root node in the middle, and finally access the right subtree
3. Post order traversal;
   First access the left subtree, then the right subtree, and finally the root node

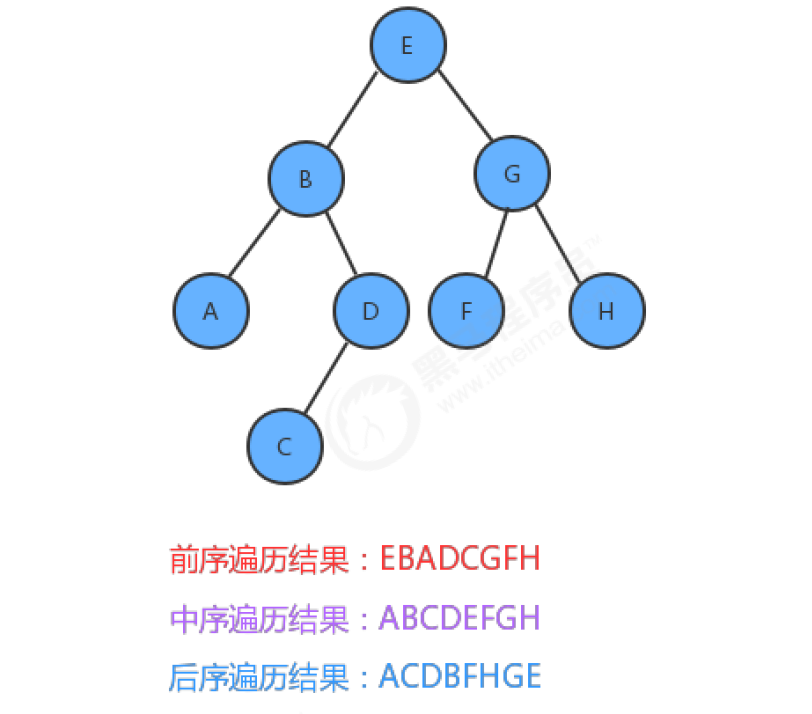
If we use three traversal methods to traverse the following trees, the results are as follows:

1. Preorder traversal

API for preorder traversal

Implementation steps:

1. Put the key of the current node into the queue;
2. Find the left subtree of the current node. If it is not empty, recursively traverse the left subtree
3. Find the right subtree of the current node. If it is not empty, recursively traverse the right subtree

Use the queue LinkedBlockingDeque provided with the jDK

code:

 //Gets all keys in the entire tree
    public Queue<Key> preErgodic(){
        Queue<Key> keys= new LinkedBlockingDeque<>();
        preErgodic(root, keys);
        return keys;
    }

    //Get all the keys of the specified tree x and put them in the keys queue
    private void preErgodic(Node x,Queue<Key> keys){
        if (x==null){
            return;
        }

        //Put the key of the x node into the keys
        keys.add(x.key);

        //Recursively traversing the left subtree of x node
        if (x.left!=null){
            preErgodic(x.left,keys);
        }

        //Recursively traversing the right subtree of x node
        if (x.right!=null){
            preErgodic(x.right,keys);
        }

    }

test

 @Test
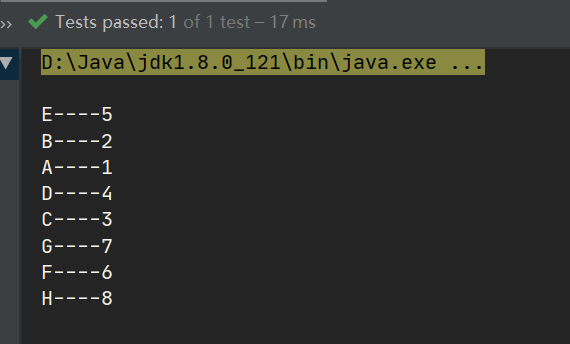
    public void test01(){
    //Create tree object
        BinaryTree<String, String> tree = new BinaryTree<>();
        //Add data to the tree
        tree.put("E", "5");
        tree.put("B", "2");
        tree.put("G", "7");
        tree.put("A", "1");
        tree.put("D", "4");
        tree.put("F", "6");
        tree.put("H", "8");
        tree.put("C", "3");

        //ergodic
        Queue<String> keys = tree.preErgodic();
        for (String key : keys) {
            String value = tree.get(key);
            System.out.println(key+"----"+value);
        }
    }

2. Middle order traversal

Middle order traversal is the most important way to traverse from small to large according to the Key

API for medium order traversal:

Implementation steps:

1. Find the left subtree of the current node. If it is not empty, recursively traverse the left subtree
2. Put the key of the current node into the queue;
3. Find the right subtree of the current node. If it is not empty, recursively traverse the right subtree

code:

   //Use middle order traversal to get all the keys in the tree
    public Queue<Key> midErgodic(){
        Queue<Key> keys = new LinkedBlockingDeque<>();
        midErgodic(root,keys);
        return keys;
    }

    //Use the middle order traversal to obtain all the keys in the specified tree x and store them in the key
    private void midErgodic(Node x,Queue<Key> keys){
        if (x==null){
            return;
        }
        //First recursion, put the keys in the left subtree into keys
        if (x.left!=null){
            midErgodic(x.left,keys);
        }
        //Put the key of the current node x into keys
        keys.add(x.key);
        //In recursion, put the keys in the right subtree into keys
        if(x.right!=null){
            midErgodic(x.right,keys);
        }

    }

Test:

 @Test
    public void test02(){
    //Create tree object
        BinaryTree<String, String> tree = new BinaryTree<>();
        //Add data to the tree
        tree.put("E", "5");
        tree.put("B", "2");
        tree.put("G", "7");
        tree.put("A", "1");
        tree.put("D", "4");
        tree.put("F", "6");
        tree.put("H", "8");
        tree.put("C", "3");

        //ergodic
        Queue<String> keys = tree.midErgodic();
        for (String key : keys) {
            String value = tree.get(key);
            System.out.println(key+"----"+value);
        }
    }

3. Post order traversal

Traversal API:

Implementation steps:

1. Find the left subtree of the current node. If it is not empty, recursively traverse the left subtree
2. Find the right subtree of the current node. If it is not empty, recursively traverse the right subtree
3. Put the key of the current node into the queue;

code:

 //Use post order traversal to return all keys in the whole tree
    public Queue<Key> afterErgodic(){
        Queue<Key> keys = new LinkedBlockingDeque<>();
        afterErgodic(root,keys);
        return keys;
    }

    //Use post order traversal to put all the keys in the specified tree x into keys
    private void afterErgodic(Node x,Queue<Key> keys){
        if (x==null){
            return ;
        }

        //Recursively put all the keys in the left subtree into keys
        if (x.left!=null){
            afterErgodic(x.left,keys);
        }
        //Recursively put all the keys in the right subtree into keys
        if (x.right!=null){
            afterErgodic(x.right,keys);
        }
        //Put the key of the x node into the keys
        keys.add(x.key);
    }

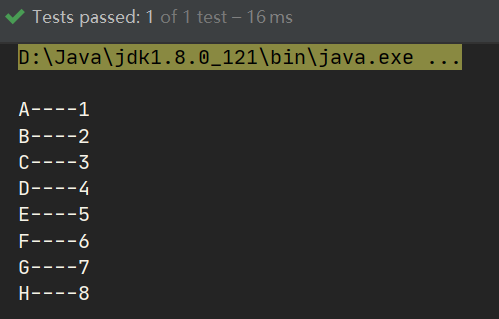
Test:

@Test
    public void test03(){
        //Create tree object
        BinaryTree<String, String> tree = new BinaryTree<>();
        //Add data to the tree
        tree.put("E", "5");
        tree.put("B", "2");
        tree.put("G", "7");
        tree.put("A", "1");
        tree.put("D", "4");
        tree.put("F", "6");
        tree.put("H", "8");
        tree.put("C", "3");

        //ergodic
        Queue<String> keys = tree.afterErgodic();
        for (String key : keys) {
            String value = tree.get(key);
            System.out.println(key+"----"+value);
        }
    }

Sequence traversal of binary tree -- breadth first

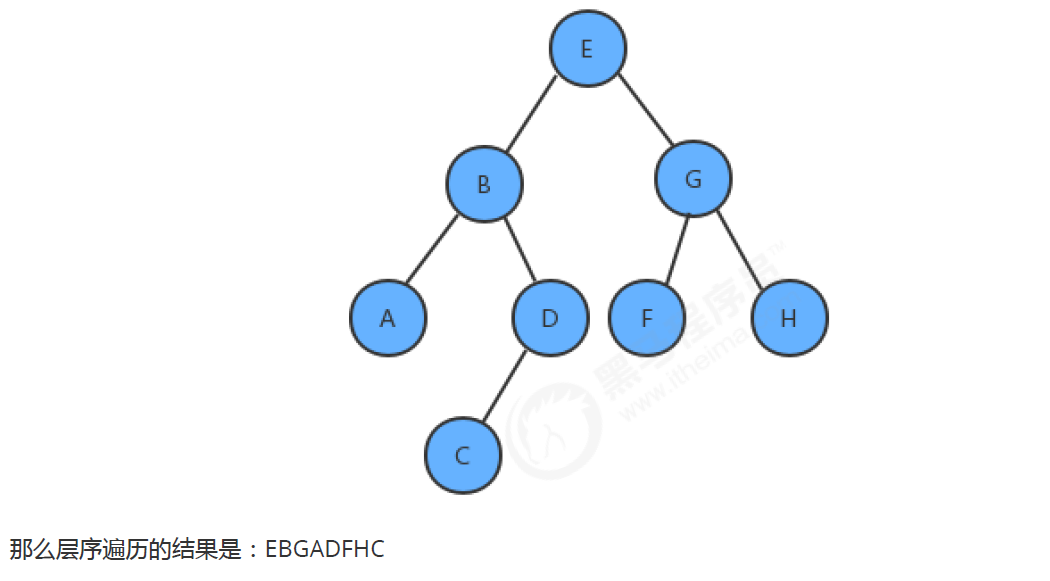
The so-called sequence traversal is to start from the root node (the first layer) and go down in turn to obtain the values of all nodes in each layer. There is a binary tree as follows

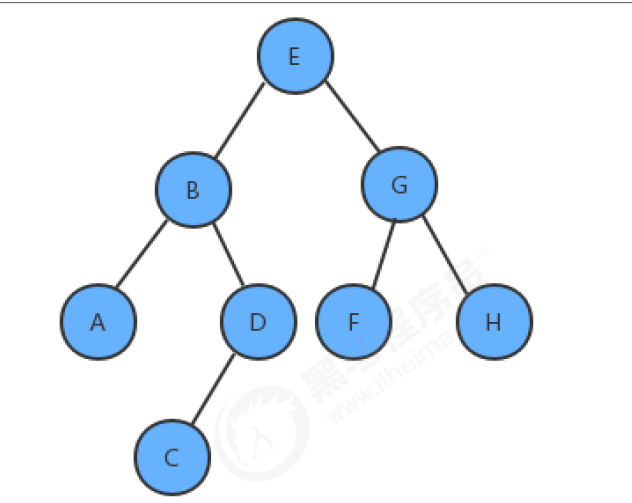
Then the result of sequence traversal is EBGADFHC

API for sequence traversal:

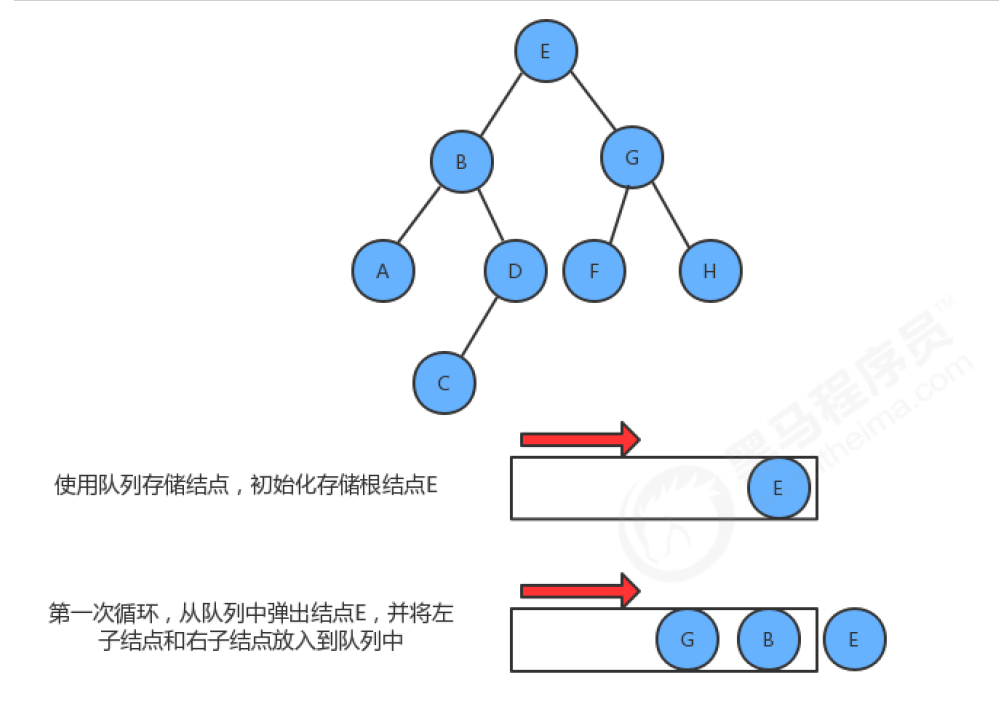
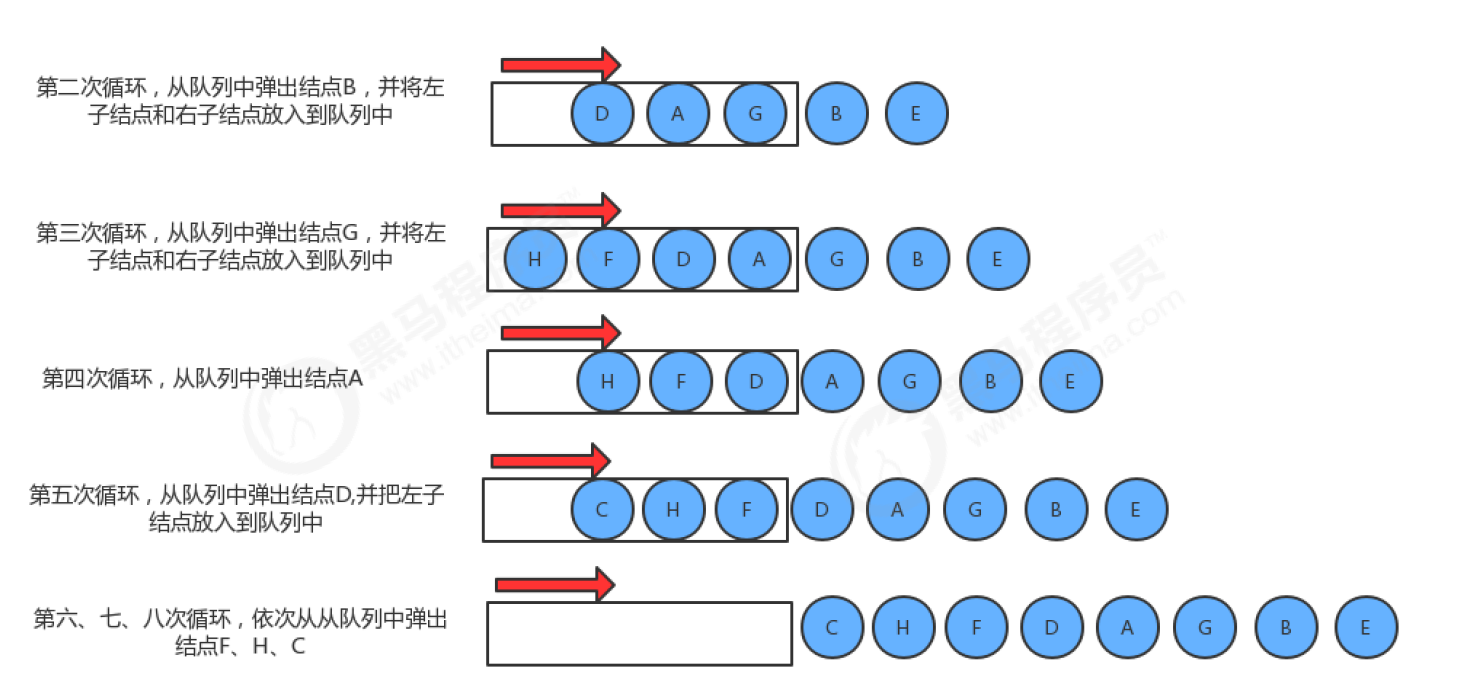
Implementation steps:

1. Create a queue to store the nodes of each layer;
2. Use the loop to pop up a node from the queue:
3. Get the key of the current node;
4. If the left child node of the current node is not empty, the left child node is put into the queue
5. If the right child node of the current node is not empty, the right child node is put into the queue

Code implementation:

    //Use sequence traversal to get all the keys in the whole tree
    public Queue<Key> layerErgodic(){
        //Define two queues to store the keys in the tree and the nodes in the tree
        Queue<Key> keys =new LinkedBlockingDeque<>();
        Queue<Node> nodes =new LinkedBlockingDeque<>();

        //By default, the root node is placed in the queue
        nodes.add(root);

        while(!nodes.isEmpty()){
            //Pop up a node from the queue and put the key into the keys
            Node n = nodes.poll();
            keys.add(n.key);
            //Judge whether the current node has left child nodes. If so, put them into nodes
            if (n.left!=null){
                nodes.add(n.left);
            }
            //Judge whether the current node has right child nodes. If so, put them into nodes
            if (n.right!=null){
                nodes.add(n.right);
            }
        }
        return keys;
    }

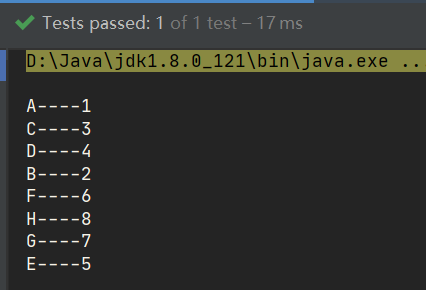
Test:

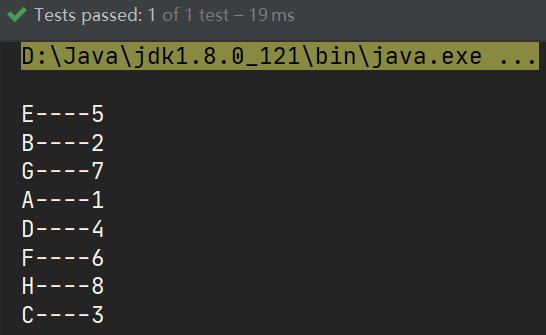
 @Test
    public void test01(){
        //Create tree object
        BinaryTree<String, String> tree = new BinaryTree<>();
        //Add data to the tree
        tree.put("E", "5");
        tree.put("B", "2");
        tree.put("G", "7");
        tree.put("A", "1");
        tree.put("D", "4");
        tree.put("F", "6");
        tree.put("H", "8");
        tree.put("C", "3");

        //ergodic
        Queue<String> keys = tree.layerErgodic();
        for (String key : keys) {
            String value = tree.get(key);
            System.out.println(key+"----"+value);
        }
    }