Binary tree

The main operation sets provided are:

• Three recursive Traversals
• Three non recursive Traversals
• level traversal
• Output leaf node
• Recursively find the height of binary tree
• Create a binary tree from an array
• Destroy binary tree
• Constructing expression tree from suffix expression

code implementation

#include <stdio.h>
#include <stdlib.h>

#include "linkQueue.c"
#include "linkStack.c"

#define BinTreeElemType char
#define NOINFO '0'

struct TreeNode {
    BinTreeElemType data;
    struct TreeNode* left;
    struct TreeNode* right;
};
typedef struct TreeNode TreeNode;
typedef struct TreeNode* BinTree;

void PreOrderTraversal_recursively(BinTree t, void (*visit)(BinTreeElemType x)) {
    if (t != NULL) {
        visit(t->data);
        PreOrderTraversal_recursively(t->left, visit);
        PreOrderTraversal_recursively(t->right, visit);
    }
}

void InOrderTraversal_recursively(BinTree t, void (*visit)(BinTreeElemType x)) {
    if (t != NULL) {
        InOrderTraversal_recursively(t->left, visit);
        visit(t->data);
        InOrderTraversal_recursively(t->right, visit);
    }
}

void PostOrderTraversal_recursively(BinTree t, void (*visit)(BinTreeElemType x)) {
    if (t != NULL) {
        PostOrderTraversal_recursively(t->left, visit);
        PostOrderTraversal_recursively(t->right, visit);
        visit(t->data);
    }
}

void PreOrderTraversal_iteratively(BinTree t, void (*visit)(BinTreeElemType x)) {
    Stack s = CreateStack();
    BinTree curr = t;
    while (curr != NULL || !StackEmpty(s)) {
        if (curr) {
            visit(curr->data);
            Push(s, curr);
            curr = curr->left;
        } else {
            Pop(s, &curr);
            curr = curr->right;
        }
    }
    DestoryStack(s);
}

void InOrderTraversal_iteratively(BinTree t, void (*visit)(BinTreeElemType x)) {
    Stack s = CreateStack();
    BinTree curr = t;
    while (curr != NULL || !StackEmpty(s)) {
        if (curr) {
            Push(s, curr);
            curr = curr->left;
        } else {
            Pop(s, &curr);
            visit(curr->data);
            curr = curr->right;
        }
    }
    DestoryStack(s);
}

void PostOrderTraversal_iteratively(BinTree t, void (*visit)(BinTreeElemType x)) {
    Stack s = CreateStack();
    BinTree curr = t;
    BinTree prev;
    while (curr != NULL || !StackEmpty(s)) {
        while (curr != NULL) {
            Push(s, curr);
            curr = curr->left;
        }
        if (!StackEmpty(s)) {
            Pop(s, &curr);
            //Conditions for accessing a node: the current passing node is a leaf node 𞓜 the right child node of the current passing node is the last visited node.
            if (curr->right == NULL || curr->right == prev) {
                visit(curr->data);
                prev = curr;
                curr = NULL;
            } else {
                Push(s, curr);
                curr = curr->right;
            }
        }
    }
    DestoryStack(s);
}

void LevelOrderTraversal(BinTree t, void (*visit)(BinTreeElemType x)) {
    if (t == NULL)
        return;
    Queue q = CreateQueue();
    BinTree curr = t;
    EnQueue(q, curr);
    while (!QueueEmpty(q)) {
        DeQueue(q, &curr);
        visit(curr->data);
        if (curr->left != NULL)
            EnQueue(q, curr->left);
        if (curr->right != NULL)
            EnQueue(q, curr->right);
    }
    DestoryQueue(q);
}

//Leaf node of output binary tree
void PreOrderPrintLeaves(BinTree t) {
    if (t != NULL) {
        if (t->left == NULL && t->right == NULL) {
            printf("%2c ", t->data);
        }
        PreOrderPrintLeaves(t->left);
        PreOrderPrintLeaves(t->right);
    }
}

//Find the height of binary tree
int BinTreeHeight(BinTree t) {
    int hl, hr;
    if (t != NULL) {
        hl = BinTreeHeight(t->left);
        hr = BinTreeHeight(t->right);
        return (hl > hr) ? (hl + 1) : (hr + 1);
    } else {
        return 0;
    }
}

BinTree CreateBinTreeFromArray(BinTreeElemType* array) {
    if (array == NULL || array[0] == NOINFO)
        return NULL;
    Queue q = CreateQueue();
    BinTree root = (BinTree)malloc(sizeof(struct TreeNode));
    root->data = array[0];
    root->left = root->right = NULL;
    EnQueue(q, root);
    BinTree t;
    int i = 1;
    while (!QueueEmpty(q)) {
        DeQueue(q, &t);
        //t's left child
        if (array[i] == NOINFO) {
            t->left = NULL;
        } else {
            t->left = (BinTree)malloc(sizeof(struct TreeNode));
            t->left->data = array[i];
            t->left->left = t->left->right = NULL;
            EnQueue(q, t->left);
        }
        i++;
        //t's right child
        if (array[i] == NOINFO) {
            t->right = NULL;
        } else {
            t->right = (BinTree)malloc(sizeof(struct TreeNode));
            t->right->data = array[i];
            t->right->left = t->right->right = NULL;
            EnQueue(q, t->right);
        }
        i++;
    }
    DestoryQueue(q);
    return root;
}

void DestoryBinTree(BinTree t) {
    if (t == NULL)
        return;
    Queue q = CreateQueue();
    BinTree curr = t;
    EnQueue(q, curr);
    while (!QueueEmpty(q)) {
        DeQueue(q, &curr);
        if (curr->left != NULL)
            EnQueue(q, curr->left);
        if (curr->right != NULL)
            EnQueue(q, curr->right);
        free(curr);
    }
    DestoryQueue(q);
}

//Construct an expression tree, assuming that the expression must be legal
BinTree ExpressionTree(const char* postExp) {
    if (postExp == NULL)
        return NULL;
    Stack s = CreateStack();
    BinTree t = (BinTree)malloc(sizeof(struct TreeNode));
    t->data = postExp[0];
    t->left = t->right = NULL;
    Push(s, t);
    for (int i = 1; postExp[i] != '\0'; ++i) {
        if (postExp[i] < 'z' && postExp[i] > 'a') {
            BinTree t = (BinTree)malloc(sizeof(struct TreeNode));
            t->data = postExp[i];
            t->left = t->right = NULL;
            Push(s, t);
        } else {
            BinTree t = (BinTree)malloc(sizeof(struct TreeNode));
            t->data = postExp[i];
            BinTree tr, tl;
            Pop(s, &tr);
            Pop(s, &tl);
            t->left = tl;
            t->right = tr;
            Push(s, t);
        }
    }
    Pop(s, &t);
    DestoryStack(s);
    return t;
}

Test code

//gcc test_binaryTree.c -o main -Wno-incompatible-pointer-types
#include <stdio.h>
#include <stdlib.h>

#include "binaryTree.c"

void visit(char ch) {
    printf("%2c ", ch);
}

void test_BinTree() {
    printf("\n%s\n", __func__);
    char arr[] = "ABCDFGI00E00H000000";
    BinTree bt = CreateBinTreeFromArray(arr);

    PreOrderTraversal_recursively(bt, visit);
    printf("\n\n");
    PreOrderTraversal_iteratively(bt, visit);
    printf("\n\n");

    InOrderTraversal_recursively(bt, visit);
    printf("\n\n");
    InOrderTraversal_iteratively(bt, visit);
    printf("\n\n");

    PostOrderTraversal_recursively(bt, visit);
    printf("\n\n");
    PostOrderTraversal_iteratively(bt, visit);
    printf("\n\n");

    LevelOrderTraversal(bt, visit);
    printf("\n\n");

    PreOrderPrintLeaves(bt);
    printf("\n\n");

    int height = BinTreeHeight(bt);
    printf("height=%d\n", height);

    char postExp[] = "abc*+de*f+g*+";
    bt = ExpressionTree(postExp);
    printf("\npostExp:%s\n", postExp);
    printf("PostOrderTraversal:\n");
    PostOrderTraversal_iteratively(bt, visit);
    printf("\n\n");
    DestoryBinTree(bt);
}

int main(int argc, char* argv[]) {
    test_BinTree();
    return 0;
}

Binary search tree

The main operation sets provided are:

• Recursive lookup and iterative lookup
• Recursive search for maximum and minimum values and iterative search for maximum and minimum values
• Insert element into BST
• Delete element from BST

code implementation

#include "binaryTree.c"

BinTree BST_Find_recursively(BinTree BST, BinTreeElemType X) {
    if (!BST) {
        return NULL;
    }
    if (X < BST->data) {
        return BST_Find_recursively(X, BST->left);
    } else if (X > BST->data) {
        return BST_Find_recursively(X, BST->right);
    } else {
        return BST;
    }
}

BinTree BST_Find_iteratively(BinTree BST, BinTreeElemType X) {
    while (BST) {
        if (X > BST->data) {
            BST = BST->right;
        } else if (X < BST->data) {
            BST = BST->left;
        } else {
            return BST;
        }
    }
    return NULL;
}

BinTree BST_FindMin_recursively(BinTree BST) {
    if (BST == NULL) {
        return NULL;
    } else if (BST->left == NULL) {
        return BST;
    } else {
        return BST_FindMin_recursively(BST->left);
    }
}

BinTree BST_FindMin_iteratively(BinTree BST) {
    if (BST) {
        while (BST) {
            BST = BST->right;
        }
    }
    return BST;
}

BinTree BST_FindMax_recursively(BinTree BST) {
    if (BST == NULL) {
        return NULL;
    } else if (BST->right == NULL) {
        return BST;
    } else {
        return BST_FindMin_recursively(BST->right);
    }
}

BinTree BST_FindMax_iteratively(BinTree BST) {
    if (BST) {
        while (BST) {
            BST = BST->right;
        }
    }
    return BST;
}

BinTree BST_Insert(BinTree BST, BinTreeElemType X) {
    if (BST == NULL) {
        BST = (BinTree)malloc(sizeof(struct TreeNode));
        BST->data = X;
        BST->right = BST->left = NULL;
    } else {
        if (X > BST->data) {
            BST->right = BST_Insert(X, BST->right);
        } else if (X < BST->data) {
            BST->left = BST_Insert(X, BST->left);
        }
    }
    return BST;
}

BinTree BST_Delete(BinTree BST, BinTreeElemType X) {
    BinTree tmp;
    if (BST == NULL) {
        return;
    } else if (X < BST->data) {
        //When X is small, it is deleted recursively to the left subtree. Pay attention to receiving the return value
        BST->left = BST_Delete(X, BST->left);
    } else if (X > BST->data) {
        //If X is large, delete it recursively from the right subtree. Pay attention to receiving the return value
        BST->right = BST_Delete(X, BST->right);
    } else {
        //The BST points to the node to be deleted
        if (!BST->left && !BST->right) {
            //The left and right subtrees are not empty. Go to the right subtree to find the minimum value
            tmp = BST_FindMin_recursively(BST->right);
            //Replacing with the current node is equivalent to deleting the current node
            BST->data = tmp->data;
            //Go to the right subtree and delete that node
            BST->right = BST_Delete(BST->data, BST->right);
        } else {
            //One or both of the left and right subtrees are empty
            tmp = BST;
            if (BST->left == NULL) {
                //If the right subtree is not empty, return it to the upper layer
                BST = BST->right;
            } else {
                //If the left subtree is not empty, return it to the upper layer
                BST = BST->left;
            }
            free(tmp);
        }
    }
    return BST;
}

Test code

nothing

balanced binary tree

Also known as AVL tree, it is a self balanced binary tree. When inserting nodes, rotate to ensure that the height difference between the left and right subtrees is ≤ 1.

code implementation

The main operation sets provided are:

• There are four balance adjustment methods: left single rotation, right single rotation, left-right rotation and right left rotation
• Insert node into AVLTree

#include <stdio.h>
#include <stdlib.h>

#include "linkQueue.c"
#define AVLTreeElemType int

struct AVLNode {
    AVLTreeElemType data;
    struct AVLNode* left;
    struct AVLNode* right;
    int height;
};
typedef struct AVLNode* AVLTree;

int max(int a, int b) {
    return (a > b) ? a : b;
}

int AVLTreeHeight(AVLTree t) {
    if (t == NULL)
        return 0;
    else
        return t->height;
}

void PrintAVLTreeLevelOrder(AVLTree t) {
    printf("\n%s\n", __func__);
    if (t == NULL)
        return;
    Queue q = CreateQueue();
    EnQueue(q, t);
    AVLTree x;
    while (!QueueEmpty(q)) {
        DeQueue(q, &x);
        printf("%2d ", x->data);
        if (x->left)
            EnQueue(q, x->left);
        if (x->right)
            EnQueue(q, x->right);
    }
    printf("\n\n");

    DestoryQueue(q);
}

//LL
AVLTree SingleLeftRotation(AVLTree A) {
    AVLTree B = A->left;
    A->left = B->right;
    B->right = A;
    A->height = max(AVLTreeHeight(A->left), AVLTreeHeight(A->right)) + 1;
    B->height = max(AVLTreeHeight(B->left), AVLTreeHeight(B->right)) + 1;
    return B;
}

//RR
AVLTree SingleRightRotation(AVLTree A) {
    AVLTree B = A->right;
    A->right = B->left;
    B->left = A;
    A->height = max(AVLTreeHeight(A->left), AVLTreeHeight(A->right)) + 1;
    B->height = max(AVLTreeHeight(B->left), AVLTreeHeight(B->right)) + 1;
    return B;
}

//LR
AVLTree DoubleLeftRightRotation(AVLTree A) {
    //First rotate the left subtree RR
    A->left = SingleRightRotation(A->left);
    //Rotate on ALL
    return SingleLeftRotation(A);
}

//RL
AVLTree DoubleRightLeftRotation(AVLTree A) {
    A->right = SingleLeftRotation(A->left);
    return SingleRightRotation(A);
}

AVLTree AVLTree_Insert(AVLTree t, AVLTreeElemType x) {
    if (t == NULL) {
        t = (AVLTree)malloc(sizeof(struct AVLNode));
        t->data = x;
        t->height = 1;
        t->left = t->right = NULL;
    } else if (x < t->data) {
        t->left = AVLTree_Insert(t->left, x);
        if (AVLTreeHeight(t->left) - AVLTreeHeight(t->right) == 2) {
            if (x < t->left->data) {
                t = SingleLeftRotation(t);
            } else {
                t = DoubleLeftRightRotation(t);
            }
        }
    } else if (x > t->data) {
        t->right = AVLTree_Insert(t->right, x);
        if (AVLTreeHeight(t->left) - AVLTreeHeight(t->right) == -2) {
            if (x > t->right->data) {
                t = SingleRightRotation(t);
            } else {
                t = DoubleRightLeftRotation(t);
            }
        }
    }  //Else x = = t - > data, no need to insert
    t->height = max(AVLTreeHeight(t->left), AVLTreeHeight(t->right)) + 1;
    return t;
}

Test code

AVL tree has good properties. We can always get a balanced binary tree by inserting nodes into the tree in any order.

//gcc test_AVLTree.c -o main -Wno-incompatible-pointer-types
#include <stdio.h>
#include <stdlib.h>

#include "AVLTree.c"

void test_AVLTree() {
    AVLTree t = NULL;
    for (int i = 0; i < 15; ++i) {
        t = AVLTree_Insert(t, i);
    }
    printf("AVLTree height=%d\n", t->height);
    PrintAVLTreeLevelOrder(t);
}

int main(int argc, char* argv[]) {
    test_AVLTree();
    return 0;
}

heap

Heap, also known as Priority Queue, is a special queue. The order in which elements are taken out is based on the priority (keyword) of elements, not the order in which elements enter the queue.

Priority queue has a wide range of uses. For example, heap sorting is the selective sorting realized by heap, and the process scheduling of the operating system. It is also necessary to select the next process to be scheduled from the ready queue according to the process priority.

Although the name is "priority queue", which sounds like a linear structure, it is generally implemented with a complete binary tree. Heap can be divided into large top heap and small top heap. As the name suggests, large top heap means that for any subtree, the root node is larger than the left and right child nodes; Small top heap is that for any subtree, the root node is smaller than the left and right child nodes. The implementation methods of the two are the same. The logical structure is a complete binary tree and is stored in array.

The following are examples of four heaps. The first two are large top heaps and the last two are small top heaps:

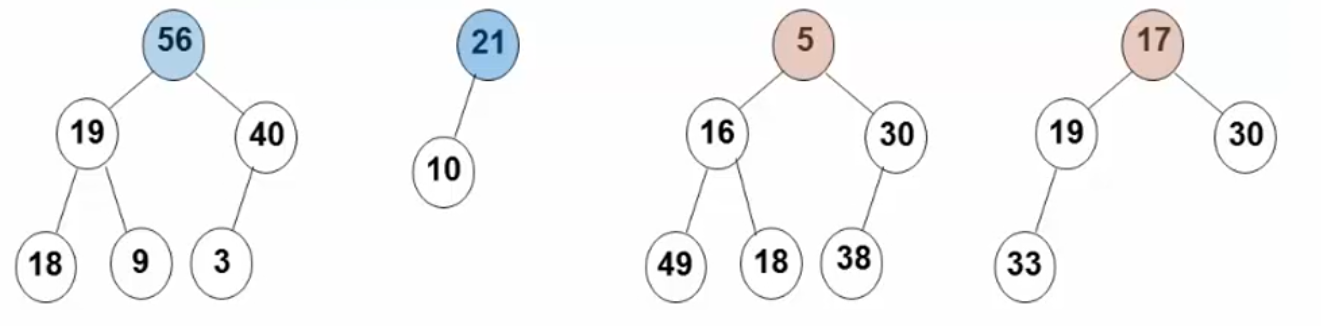
The insertion process of a large top stack is shown in the following figure:

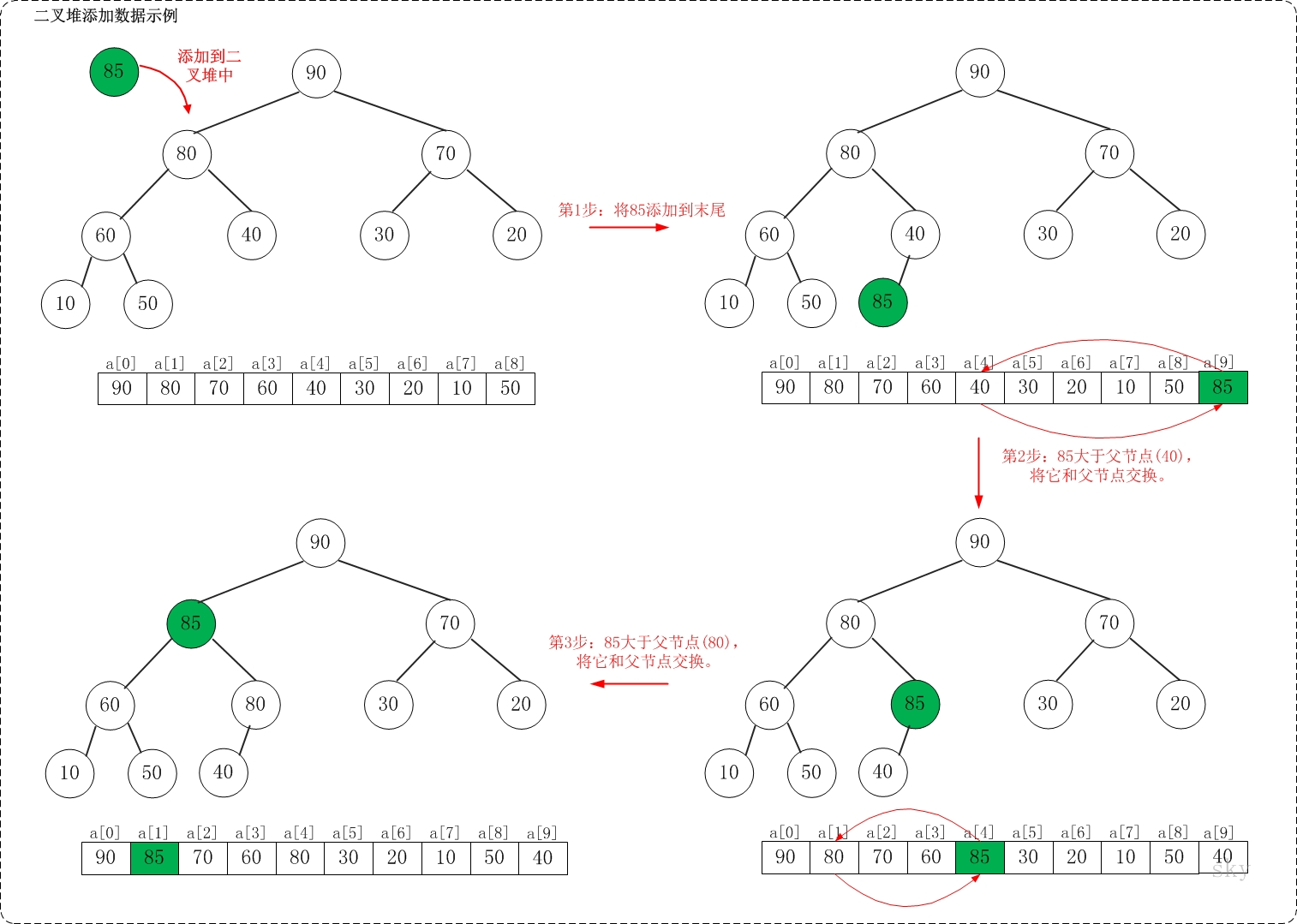
The deletion process of a large top heap is shown in the following figure:

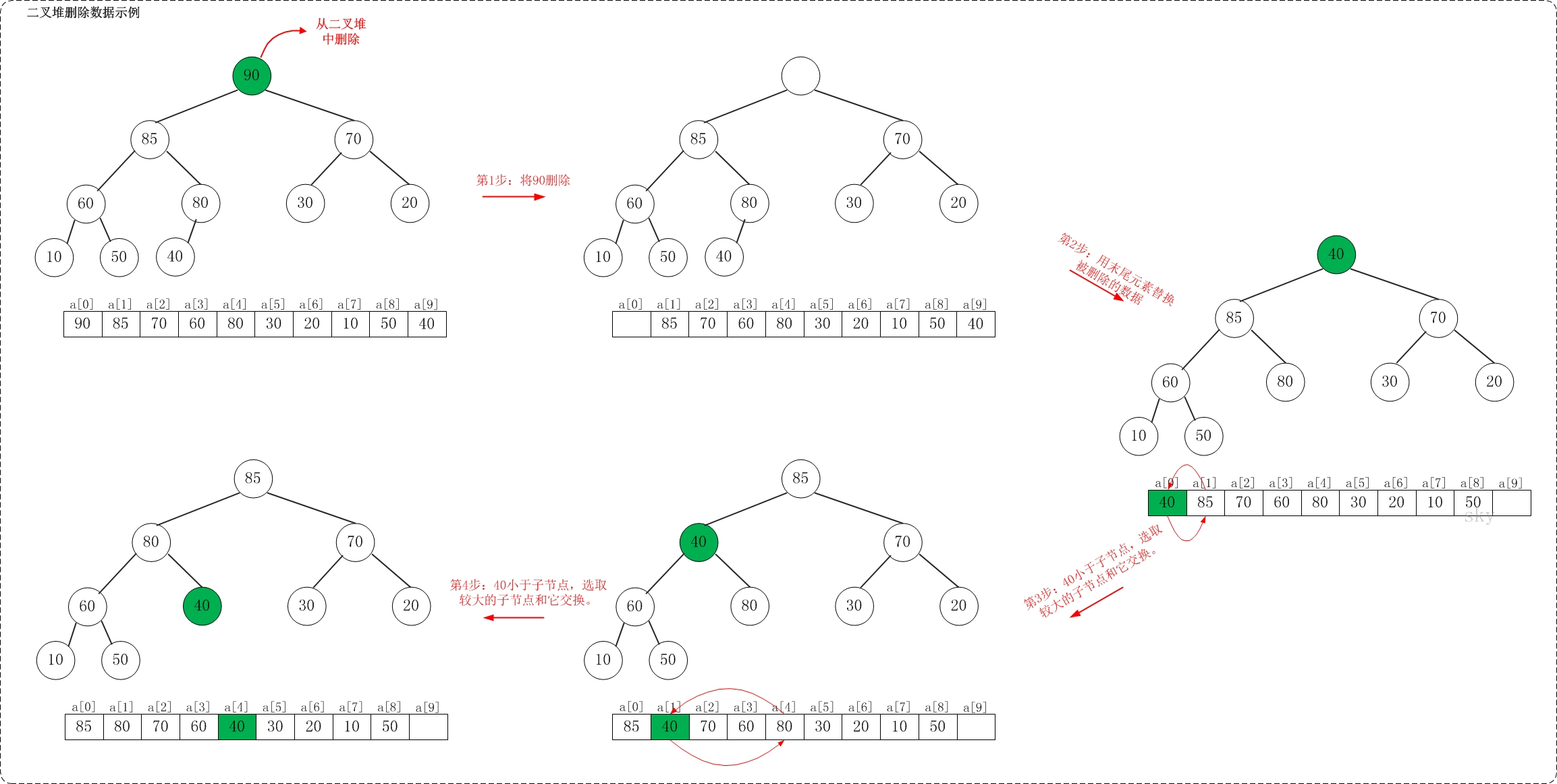
The main operation sets provided are:

• Build max / min heap
• Insert element into max / min heap
• Delete element from Max / min heap
• Filter down nodes for max / min heap
• Adjust the elements in the heap to the heap

code implementation

#include <limits.h>
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>

//Sentinel value
#define MAXDATA INT_MAX
#define MINDATA INT_MIN

typedef int HeapElemType;

struct HeapNode {
    HeapElemType* data;
    int size;
    int capacity;
};
typedef struct HeapNode* MaxHeap;
typedef struct HeapNode* MinHeap;

MaxHeap CreateMaxHeap(int MaxSize) {
    MaxHeap H = (MaxHeap)malloc(sizeof(struct HeapNode));
    //Make room for the array. Element 0 stores sentinels, so it needs + 1
    H->data = (HeapElemType*)malloc((MaxSize + 1) * sizeof(struct HeapNode));
    H->size = 0;
    H->capacity = MaxSize;
    //sentry
    H->data[0] = MAXDATA;
    return H;
}

MinHeap CreateMinHeap(int MaxSize) {
    MinHeap H = (MinHeap)malloc(sizeof(struct HeapNode));
    H->data = (HeapElemType*)malloc((MaxSize + 1) * sizeof(struct HeapNode));
    H->size = 0;
    H->capacity = MaxSize;
    H->data[0] = MINDATA;
    return H;
}

void DestoryHeap(struct HeapNode* h) {
    if (h != NULL) {
        if (h->data != NULL)
            free(h->data);
        free(h);
    }
}

bool HeapFull(struct HeapNode* H) {
    return H->size == H->capacity;
}

bool HeapEmpty(struct HeapNode* H) {
    return H->size == 0;
}

void printHeap(struct HeapNode* H) {
    printf("\n%s\n", __func__);
    for (int i = 1; i <= H->size; ++i) {
        printf("%2d ", H->data[i]);
    }
    printf("\n\n");
}

bool InsertMaxHeap(MaxHeap H, HeapElemType item) {
    if (HeapFull(H)) {
        return false;
    }
    //At first, it is assumed that the insertion position is at the end of the array
    int i = ++H->size;
    //As long as the item is larger than the parent node:
    while (item > H->data[i / 2]) {
        //Parent node down
        H->data[i] = H->data[i / 2];
        //I'll go up
        i = i / 2;
    }
    //When jumping out of the loop, i anchors the appropriate insertion position and assigns a value
    H->data[i] = item;
    return true;
}

bool InsertMinHeap(MinHeap H, HeapElemType item) {
    if (HeapFull(H)) {
        return false;
    }
    int i = ++H->size;
    while (item < H->data[i / 2]) {
        H->data[i] = H->data[i / 2];
        i = i / 2;
    }
    H->data[i] = item;
    return true;
}

HeapElemType DeleteMax(MaxHeap H) {
    if (HeapEmpty(H)) {
        return H->data[0];
    }
    HeapElemType MaxItem = H->data[1];
    HeapElemType tmp = H->data[H->size--];
    int Parent = 1;
    int Child;
    //The core of the algorithm: find the right position for tmp
    while (Parent * 2 <= H->size) {
        // Child points to the left child
        Child = 2 * Parent;
        // Child points to the largest of the left and right children
        if ((Child != H->size) && H->data[Child] < H->data[Child + 1]) {
            Child++;
        }
        //If tmp > the biggest child around, it means that tmp can sit here and jump out of the loop
        if (tmp > H->data[Child]) {
            break;
        } else {
            //Let the children come up
            H->data[Parent] = H->data[Child];
            //Go down by yourself
            Parent = Child;
        }
    }

    H->data[Parent] = tmp;
    return MaxItem;
}

HeapElemType DeleteMin(MinHeap H) {
    if (HeapEmpty(H)) {
        return H->data[0];
    }
    HeapElemType MinItem = H->data[1];
    HeapElemType tmp = H->data[H->size--];
    int Parent = 1;
    int Child;
    while (Parent * 2 <= H->size) {
        Child = 2 * Parent;
        if ((Child != H->size) && H->data[Child + 1] < H->data[Child]) {
            Child++;
        }
        if (tmp < H->data[Child]) {
            break;
        } else {
            H->data[Parent] = H->data[Child];
            Parent = Child;
        }
    }
    H->data[Parent] = tmp;
    return MinItem;
}

void percDownMaxHeap(MaxHeap H, int n) {
    HeapElemType top;
    int Child;
    int Parent = n;
    top = H->data[n];
    //Filter down
    for (Parent = n; Parent * 2 <= H->size; Parent = Child) {
        Child = 2 * Parent;
        if (Child != H->size && H->data[Child] < H->data[Child + 1]) {
            Child++;
        }
        if (top >= H->data[Child]) {
            break;
        } else {
            H->data[Parent] = H->data[Child];
        }
    }

    H->data[Parent] = top;
}

void percDownMinHeap(MinHeap H, int n) {
    HeapElemType top;
    int Child;
    int Parent = n;
    top = H->data[n];
    for (Parent = n; Parent * 2 <= H->size; Parent = Child) {
        Child = 2 * Parent;
        if (Child != H->size && H->data[Child + 1] < H->data[Child]) {
            Child++;
        }
        if (top <= H->data[Child]) {
            break;
        } else {
            H->data[Parent] = H->data[Child];
        }
    }
    H->data[Parent] = top;
}

void initMaxHeap(struct HeapNode* H) {
    //Start with the last node with a son
    for (int i = (H->size / 2); i > 0; i--) {
        percDownMaxHeap(H, i);
    }
}

void initMinHeap(struct HeapNode* H) {
    //Start with the last node with a son
    for (int i = (H->size / 2); i > 0; i--) {
        percDownMinHeap(H, i);
    }
}

Test code

#include "heap.c"

void test_MaxHeap_01() {
    printf("\n%s:\n", __func__);
    MaxHeap h0 = CreateMaxHeap(128);
    InsertMaxHeap(h0, 78);
    InsertMaxHeap(h0, 32);
    InsertMaxHeap(h0, 53);
    InsertMaxHeap(h0, 12);
    InsertMaxHeap(h0, 90);
    InsertMaxHeap(h0, 10);
    InsertMaxHeap(h0, 99);
    InsertMaxHeap(h0, 19);
    InsertMaxHeap(h0, 79);
    printHeap(h0);

    initMaxHeap(h0);
    printHeap(h0);

    while (!HeapEmpty(h0)) {
        printf("\nDeleteMax:%d\n", DeleteMax(h0));
        printHeap(h0);
    }
}

void test_MaxHeap_02() {
    printf("\n%s:\n", __func__);
    MaxHeap h0 = CreateMaxHeap(128);
    //Get something that's not a pile
    h0->data[1] = 79;
    h0->data[2] = 66;
    h0->data[3] = 43;
    h0->data[4] = 83;
    h0->data[5] = 30;
    h0->data[6] = 87;
    h0->data[7] = 38;
    h0->data[8] = 55;
    h0->data[9] = 91;
    h0->data[10] = 72;
    h0->data[11] = 49;
    h0->data[12] = 9;
    h0->size = 12;
    printHeap(h0);
    //Adjust to heap
    initMaxHeap(h0);
    printHeap(h0);
}

void test_MinHeap_01() {
    printf("\n%s:\n", __func__);
    MinHeap h0 = CreateMinHeap(128);
    InsertMinHeap(h0, 78);
    InsertMinHeap(h0, 12);
    InsertMinHeap(h0, 32);
    InsertMinHeap(h0, 53);
    InsertMinHeap(h0, 90);
    InsertMinHeap(h0, 10);
    InsertMinHeap(h0, 99);
    InsertMinHeap(h0, 19);
    InsertMinHeap(h0, 79);
    printHeap(h0);

    initMinHeap(h0);
    printHeap(h0);

    while (!HeapEmpty(h0)) {
        printf("\nDeleteMin:%d\n", DeleteMin(h0));
        printHeap(h0);
    }
}

void test_MinHeap_02() {
    printf("\n%s:\n", __func__);
    MinHeap h0 = CreateMinHeap(128);
    //Get something that's not a pile
    h0->data[1] = 79;
    h0->data[2] = 66;
    h0->data[3] = 43;
    h0->data[4] = 83;
    h0->data[5] = 30;
    h0->data[6] = 87;
    h0->data[7] = 38;
    h0->data[8] = 55;
    h0->data[9] = 91;
    h0->data[10] = 72;
    h0->data[11] = 49;
    h0->data[12] = 9;
    h0->size = 12;
    printHeap(h0);
    //Adjust to heap
    initMinHeap(h0);
    printHeap(h0);
}

int main(int argc, char* argv[]) {
    test_MaxHeap_01();
    test_MaxHeap_02();
    test_MinHeap_01();
    test_MinHeap_02();
    return 0;
}

Huffman tree

The main operation sets provided are:

• Create a Huffman tree from a DataWeightPair array

code implementation

#include <stdbool.h>
#include <stdlib.h>

#define HuffmanTreeElemType char

struct HTNode {
    int weight;
    HuffmanTreeElemType data;
    struct HTNode* left;
    struct HTNode* right;
};
typedef struct HTNode* HuffmanTree;

typedef struct {
    HuffmanTreeElemType data;
    int weight;
} DataWeightPair;

//Minimum heap for storing Huffman tree node pointers
struct MinHeapNode {
    HuffmanTree* data;
    int size;
    int capacity;
};
typedef struct MinHeapNode* MinHeap;

MinHeap CreateMinHeap(int c) {
    MinHeap h = (MinHeap)malloc(sizeof(struct MinHeapNode));
    if (h != NULL) {
        h->data = (HuffmanTree*)malloc(sizeof(HuffmanTree) * (c + 1));
        if (h->data == NULL) {
            free(h);
            return NULL;
        }
        h->capacity = c;
        h->size = 0;
        h->data[0] = (HuffmanTree)malloc(sizeof(struct HTNode));
        h->data[0]->weight = -1;
        h->data[0]->data = '\0';
    }
    return h;
}

void DestoryMinHeap(MinHeap h) {
    if (h != NULL) {
        if (h->data != NULL) {
            free(h->data);
        }
        free(h);
    }
}

bool HeapFull(MinHeap h) {
    return h->capacity == h->size;
}

bool HeapEmpty(MinHeap h) {
    return h->size == 0;
}

bool Insert(MinHeap h, HuffmanTree x) {
    if (HeapFull(h))
        return false;
    int i = ++h->size;
    for (; x->weight < h->data[i / 2]->weight; i /= 2) {
        h->data[i] = h->data[i / 2];
    }
    h->data[i] = x;
    return true;
}

void percDown(MinHeap h, int p) {
    int parent = p;
    int child;
    HuffmanTree x = h->data[p];
    for (parent = p; parent * 2 <= h->size; parent = child) {
        child = parent * 2;
        if (child != h->size && h->data[child + 1]->weight < h->data[child]->weight)
            child++;
        if (h->data[parent]->weight < h->data[child]->weight)
            break;
        else
            h->data[parent] = h->data[child];
    }
    h->data[parent] = x;
}

HuffmanTree DeleteMin(MinHeap h) {
    if (h == NULL || HeapEmpty(h)) {
        return NULL;
    }
    HuffmanTree minItem = h->data[1];
    HuffmanTree x = h->data[h->size--];
    int parent, child;
    for (parent = 1; parent * 2 <= h->size; parent = child) {
        child = parent * 2;
        if (child != h->size && h->data[child + 1]->weight < h->data[child]->weight)
            child++;
        if (x->weight <= h->data[child]->weight)
            break;
        else
            h->data[parent] = h->data[child];
    }
    h->data[parent] = x;
    return minItem;
}

void initMinHeap(MinHeap h) {
    for (int i = h->size / 2; i >= 1; --i) {
        percDown(h, i);
    }
}

HuffmanTree CreateHuffmanTree(const DataWeightPair* dfps, int n) {
    int i;
    HuffmanTree T;

    MinHeap h = CreateMinHeap(n * 2);
    for (i = 0; i < n; ++i) {
        h->data[i + 1] = (HuffmanTree)malloc(sizeof(struct HTNode));
        h->data[i + 1]->data = dfps[i].data;
        h->data[i + 1]->weight = dfps[i].weight;
    }
    h->size = n;
    initMinHeap(h);

    for (i = 0; i < n - 1; ++i) {
        T = (HuffmanTree)malloc(sizeof(struct HTNode));
        T->left = DeleteMin(h);
        T->right = DeleteMin(h);
        T->weight = T->left->weight + T->right->weight;
        T->data = '\0';
        Insert(h, T);
    }
    T = DeleteMin(h);
    return T;
}

Test code

#include <stdio.h>
#include <stdlib.h>

#include "huffmanTree.c"

void printHuffmanTree_preOrder(HuffmanTree ht) {
    if (ht) {
        printf("data=%c,weight=%d\n", ht->data, ht->weight);
        printHuffmanTree_preOrder(ht->left);
        printHuffmanTree_preOrder(ht->right);
    }
}

void printHuffmanTree_inOrder(HuffmanTree ht) {
    if (ht) {
        printHuffmanTree_inOrder(ht->left);
        printf("data=%c,weight=%d\n", ht->data, ht->weight);
        printHuffmanTree_inOrder(ht->right);
    }
}

void printHuffmanTreeLeaves(HuffmanTree ht) {
    if (ht) {
        if (ht->left == NULL && ht->right == NULL) {
            printf("data=%c,weight=%d\n", ht->data, ht->weight);
        }
        printHuffmanTreeLeaves(ht->left);
        printHuffmanTreeLeaves(ht->right);
    }
}

void test_huffmanTree() {
    DataWeightPair dfps[7] = {
        {'a', 10},
        {'e', 15},
        {'i', 12},
        {'s', 3},
        {'t', 4},
        {'p', 13},
        {'l', 1}

    };

    HuffmanTree ht = CreateHuffmanTree(dfps, 7);

    printf("\npreOrder\n");
    printHuffmanTree_preOrder(ht);

    printf("\ninOrder\n");
    printHuffmanTree_inOrder(ht);

    printf("\nleaves\n");
    printHuffmanTreeLeaves(ht);
    return;
}

int main(int argc, char* argv[]) {
    test_huffmanTree();
    return 0;
}

Joint search set

The main operation sets provided are:

• Common search algorithm and path compression search algorithm
• Ordinary union algorithm and rank merging union algorithm

code implementation

#define MAXSETSIZE 1024
#include <stdbool.h>

typedef int SetElemType;
typedef int SetName;
typedef SetElemType* SetType;

//Look up the parent node pointer until you find the root node
SetName Find(SetType S, SetElemType X) {
    while (S[X] >= 0)
        X = S[X];
    return X;
}

SetName Find_PathCompression(SetType S, SetElemType X) {
    if (S[X] < 0)
        return X;
    else
        return S[X] = Find(S, S[X]);
}

void Union_tssn(SetType S, SetName Root1, SetName Root2) {
    //The default Root1 and Root2 are the root nodes of two different collections
    S[Root2] = Root1;
}

void Union_mergeByHeight(SetType S, SetName Root1, SetName Root2) {
    if (S[Root2] < S[Root1]) {
        //If set 2 is high, set 1 is merged into set 2
        S[Root1] = Root2;
    } else {
        //otherwise
        if (S[Root1] == S[Root2])
            S[Root1]--;
        S[Root2] = Root1;
    }
}

void Union_mergeBySize(SetType S, SetName Root1, SetName Root2) {
    if (S[Root2] < S[Root1]) {
        //If set 2 is large
        S[Root2] += S[Root1];
        //Merge set 1 into set 2
        S[Root1] = Root2;
    } else {
        //Otherwise, set 1 is large
        S[Root1] += S[Root2];
        //Merge set 2 into set 1
        S[Root2] = Root1;
    }
}

Test code

nothing