"Tree" of data structure

1, Theory

1. Introduction to tree

• Tree is an abstract model of hierarchical data
• Common trees: DOM tree, cascade selection, tree control
• js does not have a tree, but you can use Object and Array to build a tree
• Common operations of tree: depth / breadth first traversal, middle first and then order traversal

2. Depth / breadth first traversal

const tree = {
  val: 'a',
  children: [{
    val: 'b',
    children: [{
      val: 'd',
      children: [],
    },{
      val: 'e',
      children: [],
    }],
  },{
    val: 'c',
    children: [{
      val: 'f',
      children: [],
    },{
      val: 'g',
      children: [],
    }],
  }],
}

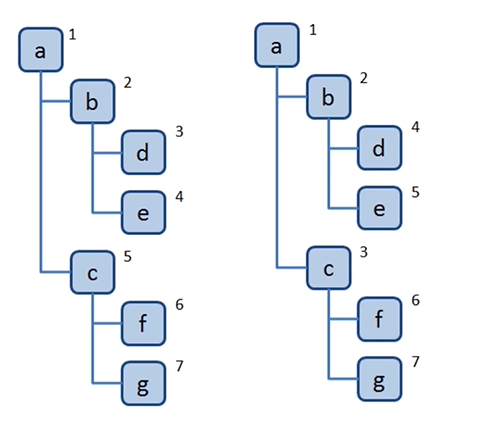
• Depth first traversal: branches of the search tree as deep as possible
• Breadth first traversal: first visit the node closest to the root node

2.1 depth first traversal

• recursion

2.1.1 algorithm formula

1. Access root node
2. Perform depth first traversal of the children of the root node one by one

2.1.2 coding part

// dfs
const DFS = root => {
  console.log(root.val)
  root.chileren.forEach(child => DFS(child))
// abdecfg

2.2 breadth first traversal

• queue

2.1.1 algorithm formula

1. Create a new queue and queue the root node
2. Team leader out of the team and visit
3. Join the children at the head of the team one by one
4. Repeat 2 and 3 until the queue is empty

2.1.2 coding part

// bfs
const BFS = root => {
  const q = [root]
  while(q.length) {
    const n = q.shift()
    console.log(n.val)
    n.children.forEach(child => q.push(child))
  }
}
// abcdefg

3. Traversal of binary tree from middle to last (recursion)

3.1 what is a binary tree

// bt
const bt = {
  val: 1,
  left: {
    val: 2,
    left: {
      val: 4,
      left: null,
      right: null
    },
    right: {
      val: 5,
      left: null,
      right: null
    }
  },
  right: {
    val: 3,
    left: {
      val: 6,
      left: null,
      right: null
    },
    right: {
      val: 7,
      left: null,
      right: null
    }
  }
}

• Each node in the tree can have at most two child nodes
• js usually uses Object to simulate binary tree

3.2 preorder traversal

3.2.1 formula of preorder traversal algorithm

1. Access root node
2. First traverse the left subtree of the root node
3. The right subtree of the root node is traversed first

3.2.2 coding part

// preorder
const preorder = root => {
  if(!root) return
  console.log(root.val)
  preorder(root.left)
  preorder(root.right)
}

3.3 middle order traversal

3.3.1 middle order traversal algorithm formula

1. Middle order traversal of the left subtree of the root node
2. Access root node
3. Middle order traversal of the right subtree of the root node

3.3.2 coding part

// inorder
const inorder = root => {
  if(!root) return
  inorder(root.left)
  console.log(root.val)
  inorder(root.right)
}

3.4 post order traversal

3.4.1 postorder traversal algorithm formula

1. Middle order traversal of the left subtree of the root node
2. Middle order traversal of the right subtree of the root node
3. Access root node

3.4.2 coding part

// postorder
const postorder = root => {
  if(!root) return
  postorder(root.left)
  postorder(root.right)
  console.log(root.val)
}

4. Traversal of binary tree (non recursive)

• stack

4.1 preorder traversal

coding part

// preorder
const preorder = root => {
  if(!root) return
  const stack = [root]
  while(stack.length) {
    const n = stack.pop()
    console.log(n.val)
    if(n.right) stack.push(n.right)
    if(n.left) stack.push(n.left)
  }
}

4.2 middle order traversal

coding part

// inorder
const inorder = root => {
  if(!root) return
  const stack = []
  let p = root
  while(stack.length || p) {
    while(p) {
      stack.push(p)
      p = p.left
    }
    const n = stack.pop()
    console.log(n.val)
    p = n.right
  }
}

4.3 post order traversal

coding part

// postorder
const postorder = root => {
  if(!root) return
  const stack = [root]
  const outputStack = []
  while(stack.length) {
    const n = stack.pop()
    outputStack.push(n)
    if(n.left) stack.push(n.left)
    if(n.right) stack.push(n.right)
  }
  while(outputStack.length) {
    const n = outputStack.pop()
    console.log(n.val)
  }
}

2, Brush questions

1. Maximum depth of binary tree (104)

1.1 Title Description

• Given a binary tree, find its maximum depth
• The depth of the binary tree is the number of nodes on the longest path from the root node to the farthest leaf node
• Note: leaf nodes refer to nodes without child nodes

1.2 problem solving ideas

• Find the maximum depth and consider depth first traversal
• In the process of depth first traversal, record the level of each node and find the largest level

1.3 problem solving steps

• Maximum depth of new variable record
• Depth first traverses the whole tree and records the hierarchy of each node, constantly refreshing the maximum depth
• Maximum depth returned at the end of traversal

function maxDepth(root) {
  let res = 0
  const dfs = (n, l) => {
    if(!n) return
    if(!n.left && !n.right) {
      res = Math.max(res, l)
    }
    dfs(n.left, l+1)
    dfs(n.right, l+1)
  }
  dfs(root, 1)
  return res
}

1.4 time complexity & space complexity

• Time complexity: O(n)
• Space complexity: O(logn)~O(n)

2. Minimum depth of binary tree (111)

2.1 Title Description

• Given a binary tree, find its minimum depth
• The minimum depth is the number of nodes on the shortest path from the root node to the nearest leaf node
• Note: leaf nodes refer to nodes without child nodes

2.2 problem solving ideas

• Find the minimum depth and consider breadth first traversal
• In the breadth first traversal process, if a leaf node is encountered, stop the traversal and return to the node level

2.3 problem solving steps

• Breadth first traverses the whole tree and records the hierarchy of each node
• When a leaf node is encountered, return to the node level and stop traversal

function minDepth(root) {
  if(!root) return 0
  const q = [[root, 1]]
  while(q.length) {
    const [n, l] = q.shift()
    if(!n.left && !n.right) {
      return l
    }
    if(n.left) q.push([n.left, l+1])
    if(n.right) q.push([n.right, l+1])
  }
}

2.4 time complexity & space complexity

• Time complexity: O(n)
• Space complexity: O(n)

3. Sequence traversal of binary tree (102)

3.1 Title Description

• Give you the root node of the binary tree, root, and return the sequence traversal of its node value
• That is, access all nodes from left to right layer by layer

3.2 problem solving ideas

Input: root = [3,9,20,null,null,15,7]
Output: [[3], [9,20], [15,7]]

• Sequence traversal order is breadth first traversal
• The hierarchy of each node shall be recorded during traversal

3.3 problem solving steps

• breadth-first search
• The hierarchy of each node shall be recorded during traversal

function levelOrder(root) {
  if(!root) return []
  const q = [[root, 0]]
  const res = []
  while(q.length) {
    const [n, level] = q.shift()
    if(!res[level]) {
      res.push([n.val])
    } else {
      res[level].push(n.val)
    }
    if(n.left) q.push([n.left, level+1])
    if(n.right) q.push([n.right, level+1])
  }
  return res
}

Method 2

function levelOrder(root) {
  if(!root) return []
  const q = [root]
  const res = []
  while(q.length) {
    let len = q.length
    res.push([])
    while(len--) {
      const n = q.shift()
      res[res.length-1].push(n.val)
      if(n.left) q.push(n.left)
      if(n.right) q.push(n.right)
    }
  }
  return res
}

3.4 time complexity & space complexity

• Time complexity: O(n)
• Space complexity: O(n)

4. Middle order traversal of binary tree (94)

4.1 Title Description

• Given the root node of a binary tree, root, returns its middle order traversal
• Advanced: recursive algorithm is very simple. Can you complete it through iterative algorithm?

4.2 problem solving

function inorderTraversal(root) {
  const res = []
  const rec = n => {
    if(!n) return
    rec(n.left)
    res.push(n.val)
    rec(n.right)
  }
  rec(root)
  return res
}

Method 2

function inorderTraversal(root) {
  const res = []
  const stack = []
  let p = root
  while(stack.length || p) {
    while(p) {
      stack.push(p)
      p = p.left
    }
    const n = stack.pop()
    res.push(n.val)
    p = n.right
  }
  return res
}

4.3 time complexity & space complexity

• Time complexity: O(n)
• Space complexity: O(n)

5. Path sum (112)

5.1 Title Description

• Given a binary tree and a target sum
• Judge whether there is a path from the root node to the leaf node in the tree. The sum of all node values on this path is equal to the target sum
• If it exists, return true; Otherwise, false is returned

5.2 problem solving ideas

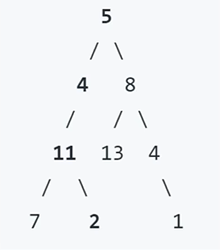
Input: root = [5,4,8,11, null, 13,4,7,2, null, null, 1], targetsum = 22
Output: true

• During depth first traversal, record the current path node value and
• At the leaf node, judge whether the node value sum of the current path = target sum

5.3 problem solving steps

• Depth first traverses the binary tree. At the leaf node, judge whether the node value sum of the current path = target sum. If yes, return true
• After traversal, if there is no match, false is returned

function hasPathSum(root, sum) {
  if(!root) return false
  let res = false
  const dfs = (n, s) => {
    if(!n.left && !n.right && s === sum) {
      res = true
    } 
    if(n.left) dfs(n.left, s + n.left.val)
    if(n.right) dfs(n.right, s + n.right.val)
  }
  dfs(root, root.val)
  return res
}

Method 2

function levelOrder(root) {
  if(!root) return []
  const q = [root]
  const res = []
  while(q.length) {
    let len = q.length
    res.push([])
    while(len--) {
      const n = q.shift()
      res[res.length-1].push(n.val)
      if(n.left) q.push(n.left)
      if(n.right) q.push(n.right)
    }
  }
  return res
}

5.4 time complexity & space complexity

• Time complexity: O(n)
• Space complexity: O(logn)~O(n)

6 traverse all node values of json (front end and tree)

const json = {
  a: { b: { c: 1 } },
  d: [1, 2]
}

6.1 coding part

const dfs = (n, path) => {
  console.log(n, path)
  Object.keys(n).forEach(k => {
    dfs(n[k], path.concat(k))
  })
}

3, Summary - technical points

• Tree is an abstract model of hierarchical data, which is widely used in the front end
• Common operations of tree: depth / breadth first traversal, middle first and then order traversal