tree
Tree is a nonlinear data structure.
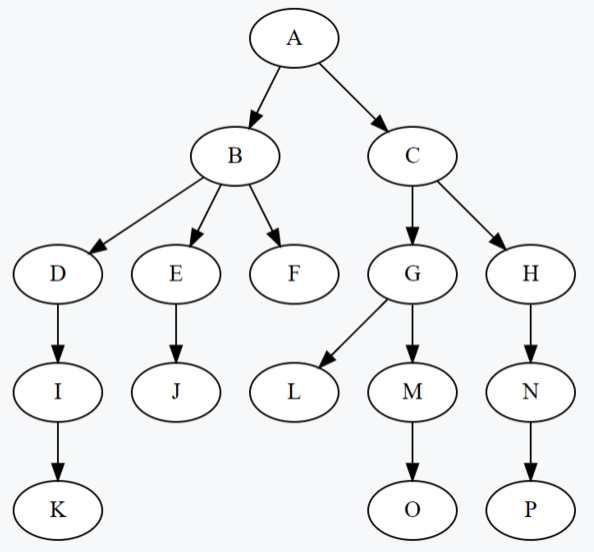
In the tree, each node contains its own value and its connected child nodes. The line connecting the nodes is called edge. As shown in the following figure, a is the root node and the parent node of B and C, that is, both B and C are child nodes of A. Similarly, B is the parent node of D and E, and so on. Note that H, I, J, F, and G are all leaf node s because they are located at the bottom of the tree without any child nodes.
Tree features:
- Each node has only limited or no child nodes;
- A node without a parent node is called a root node;
- Each non root node has only one parent node;
- In addition to the root node, each child node can be divided into multiple disjoint subtrees;
- There are no cycles in the tree
Related terms
- Node: the basic part of the tree; Each node has a name or key value. The node can also save additional data items, which vary according to different applications;
- Edge: each edge connects exactly two nodes, indicating that there is association between nodes, and the edge has access direction;
- Root: the only node in the tree without an edge;
- Path: an ordered list of nodes connected together by edges in turn;
Types of trees:
- Binary tree: a tree with at most two subtrees per node is called a binary tree;
- Complete binary tree: for a binary tree, suppose its depth is d (d > 1). In addition to layer D, the number of nodes in other layers has reached the maximum, and all nodes in layer D are continuously and closely arranged from left to right. Such a binary tree is called a complete binary tree;
- Full binary tree: a complete binary tree with all leaf nodes at the bottom;
- Balanced binary tree (AVL tree): if and only if the height difference between two subtrees of any node is not greater than 1;
- Sorted binary tree (binary search tree): also known as binary search tree and ordered binary tree;
- B-tree: a self balanced binary search tree that optimizes read and write operations. It can keep data in order and has more than two subtrees.
Implementation of nested list method
Python List to implement binary tree data structure, [root, left, right].
Advantages of nested list method:
The structure of subtree is the same as that of tree, which is a recursive data structure;
It is easy to extend to multi fork tree, and only need to add list elements;
def BinaryTree(r):
return [r, [], []]
def insertLeft(root,newBranch):
t = root.pop(1)
if len(t) > 1:
root.insert(1, [newBranch, t, []])
else:
root.insert(1, [newBranch, [], []])
return root
def insertRight(root,newBranch):
t = root.pop(2)
if len(t) > 1:
root.insert(2,[newBranch,[],t])
else:
root.insert(2,[newBranch,[],[]])
return root
def getRootVal(root):
return root[0]
def setRootVal(root,newVal):
root[0] = newVal
def getLeftChild(root):
return root[1]
def getRightChild(root):
return root[2]
r = BinaryTree(3)
print("r = BinaryTree(3): ",r)
insertLeft(r,4)
print("insertLeft(r,4): ",r)
insertLeft(r,5)
print("insertLeft(r,5): ",r)
insertRight(r,6)
print("insertRight(r,6): ",r)
insertRight(r,7)
print("insertRight(r,7): ",r)
l = getLeftChild(r)
print("l = getLeftChild(r): ",l)
setRootVal(l,9)
print("setRootVal(l,9): ",r)
insertLeft(l,11)
print("insertLeft(l,11): ",r)
print("getRightChild(getRightChild(r)): ",getRightChild(getRightChild(r)))
Output results: r = BinaryTree(3): [3, [], []] insertLeft(r,4): [3, [4, [], []], []] insertLeft(r,5): [3, [5, [4, [], []], []], []] insertRight(r,6): [3, [5, [4, [], []], []], [6, [], []]] insertRight(r,7): [3, [5, [4, [], []], []], [7, [], [6, [], []]]] l = getLeftChild(r): [5, [4, [], []], []] setRootVal(l,9): [3, [9, [4, [], []], []], [7, [], [6, [], []]]] insertLeft(l,11): [3, [9, [11, [4, [], []], []], []], [7, [], [6, [], []]]] getRightChild(getRightChild(r)): [6, [], []]
Node connection method

Each node stores the data items of the root node and links to the left and right subtrees.
class BinaryTree:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def insertLeft(self,newNode):
if self.left == None:
self.left = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.left = self.left
self.left = t
def insertRight(self,newNode):
if self.right == None:
self.right = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.right = self.right
self.right = t
def getRightChild(self):
return self.right
def getLeftChild(self):
return self.left
def setRootVal(self,val):
self.val = val
def getRootVal(self):
return self.val
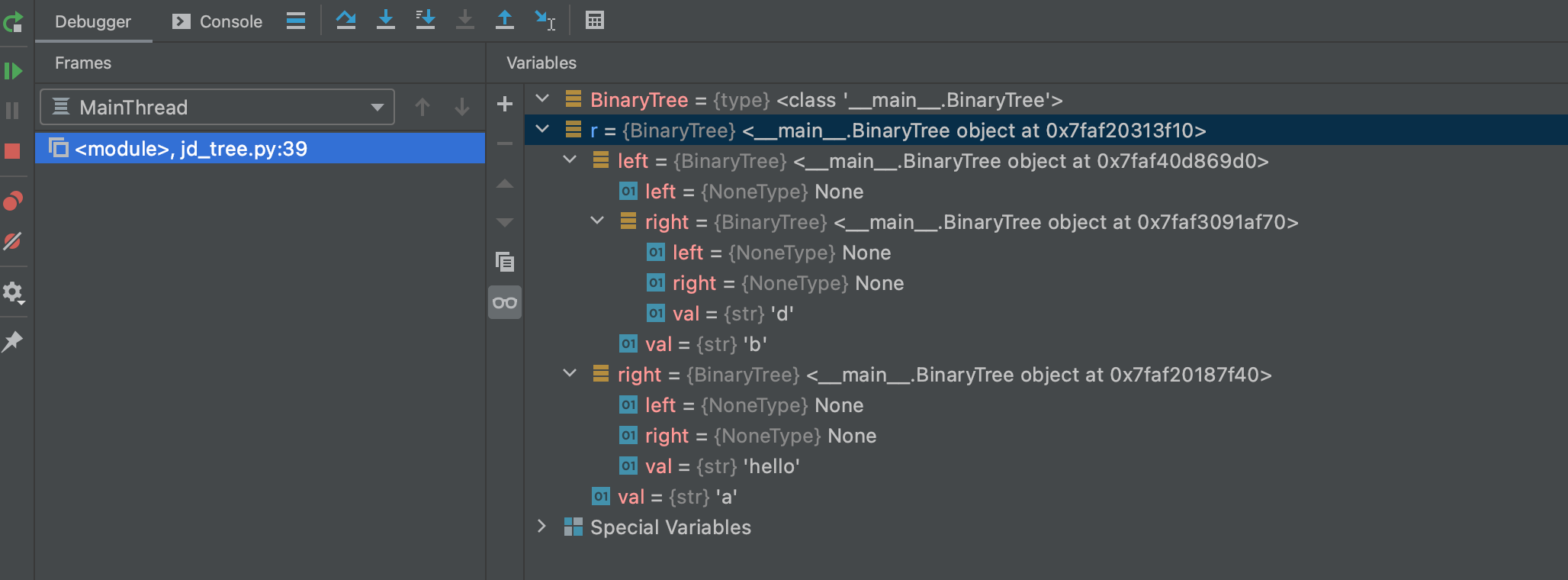
r = BinaryTree('a')
r.insertLeft('b')
r.insertRight('c')
r.getRightChild().setRootVal('hello')
r.getLeftChild().insertRight('d')
Application of tree
Expression parse tree
Rule: scan each word of the full parenthesis expression from left to right, and establish the parsing number according to the rule.
- If the current word is "(": add a new node for the current node as its left child node, and the current node will drop to this new node;
- If the current word is the operator "+, -, *, /": set the value of the current node as the symbol, add a new node for the current node as its right child node, and the current node will drop to this new node;
- If the current word is an operand: set the value of the current node to this number, and the current node rises to the parent node;
- If the current word is "): when the money node rises to the parent node;
To create an expression parse tree:
- To create left and right subtrees, you can call insertLeft/Right;
- setRootVal can be called to set the value of the current node;
- Drop to the left and right subtrees and call getLeft/RightChild;
- When we rise to the parent node, we need to use a stack to record and track the parent node;
When the current node descends, the node before the descent is push ed into the stack. When the current node needs to rise to the parent node, it can rise to the pop out of the stack node.
def buildParseTree(fpexp):
fplist = fpexp.split()
pStack = Stack()
eTree = BinaryTree('')
pStack.push(eTree)
curTree = eTree
for i in fplist:
if i == "(":
curTree.insertLeft('')
pStack.push(curTree)
curTree = curTree.getLeftChild()
elif i not in ['+','-','*','/',')']:
curTree.setRootVal(int(i))
parent = pStack.pop()
curTree = parent
elif i in ['+','-','*','/']:
curTree.setRootVal(i)
curTree.insertRight('')
pStack.push(curTree)
curTree = curTree.getRightChild()
elif i == ')':
curTree = pStack.pop()
else:
raise ValueError
return eTree
buildParseTree("( 2 + ( 3 * 5 ) )")

Evaluation using expression parse tree
- Basic end condition: the leaf node is the simplest subtree without left and right child nodes, and the data item of its root node is the value of the child expression tree;
- Downsizing: divide the expression tree into left subtree and right subtree, that is, downsizing;
- Call itself: call evaluate to calculate the values of the left and right subtrees respectively, and then calculate the values of the left and right subtrees according to the operators of the root node to obtain the value of the expression;
import operator op = operator.add n = op(1,2) print(n)
Output: 2
import operator
def evaluate(parseTree):
ops = {'+':operator.add,'-':operator.sub,'*':operator.mul,'/':operator.truediv}
leftC = parseTree.getLeftChild()
rightC = parseTree.getRightChild()
if leftC and rightC:
fn = ops[parseTree.getRootVal()]
return fn(evaluate(leftC),evaluate(rightC))
else:
return parseTree.getRootVal()