Binary sort tree

Binary sort tree is also called binary search tree and binary search tree. Defined as:

Properties of binary sort tree:

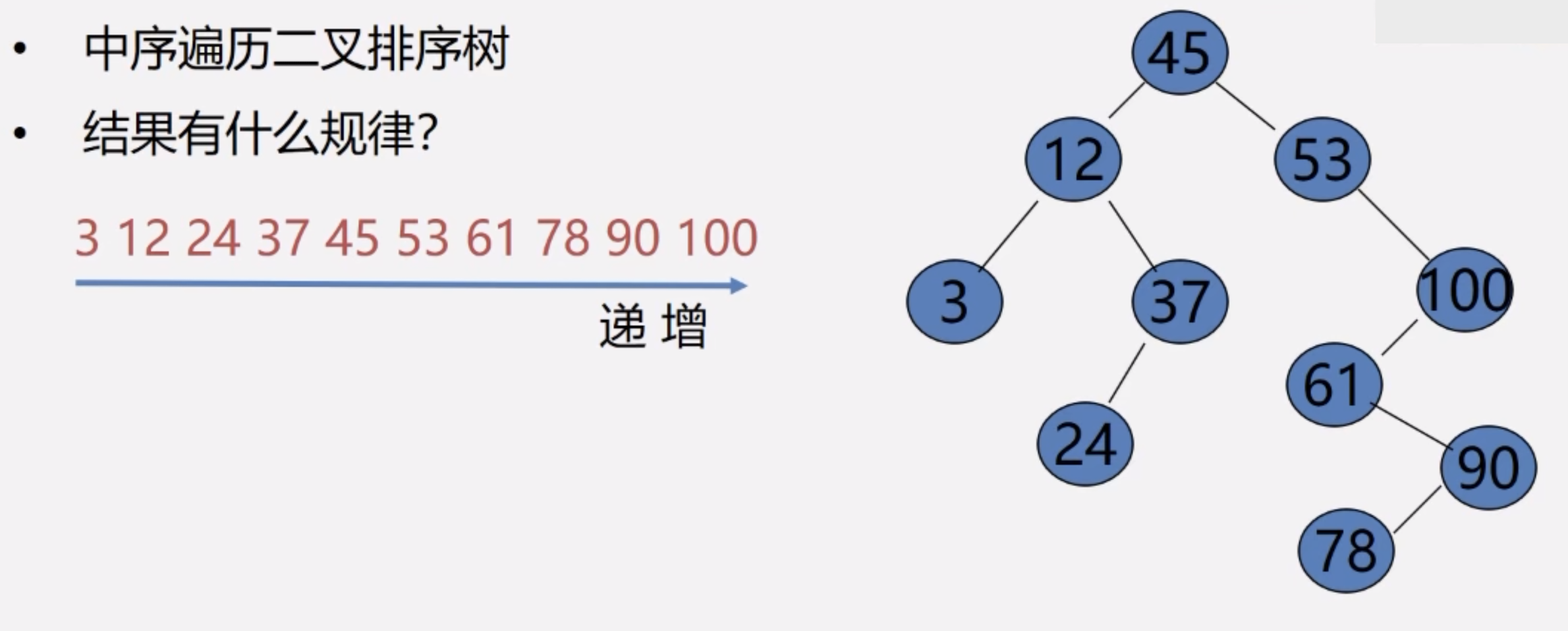
The sequence of data elements obtained by traversing a non empty binary sort tree in middle order is an incremental ordered sequence arranged by keywords.

Storage structure of binary sort tree

typedef int KeyType;
typedef struct{
    KeyType key;
    /*...Other data fields*/ 
} ElemType;
typedef struct BSTNode{
    ElemType data;
    struct BSTNode *lChild;
    struct BSTNode *RChild;
} BSTNode, *BSTree;//Binary sort tree node type (binary linked list)

Search of binary sort tree

BSTree SearchBST(BSTree T, KeyType x)//recursive algorithm
{
    if (T == NULL || T->data.key == x) return T;//Return the address of the node to be found
    else if (x < T->data.key) return SearchBST(T->lChild, x);//Continue searching in the left subtree
    else return SearchBST(T->RChild, x);//Continue searching in the right subtree
}

BSTNode* SearchBST2(BSTree T, KeyType x)//non-recursive algorithm 
{
    BSTNode *p = T;
    while (p)
    {
        if (p->data.key == x) return p;
        else if (p->data.key < x) p = p->RChild;
        else p = p->lChild;
    }
    return NULL;
}

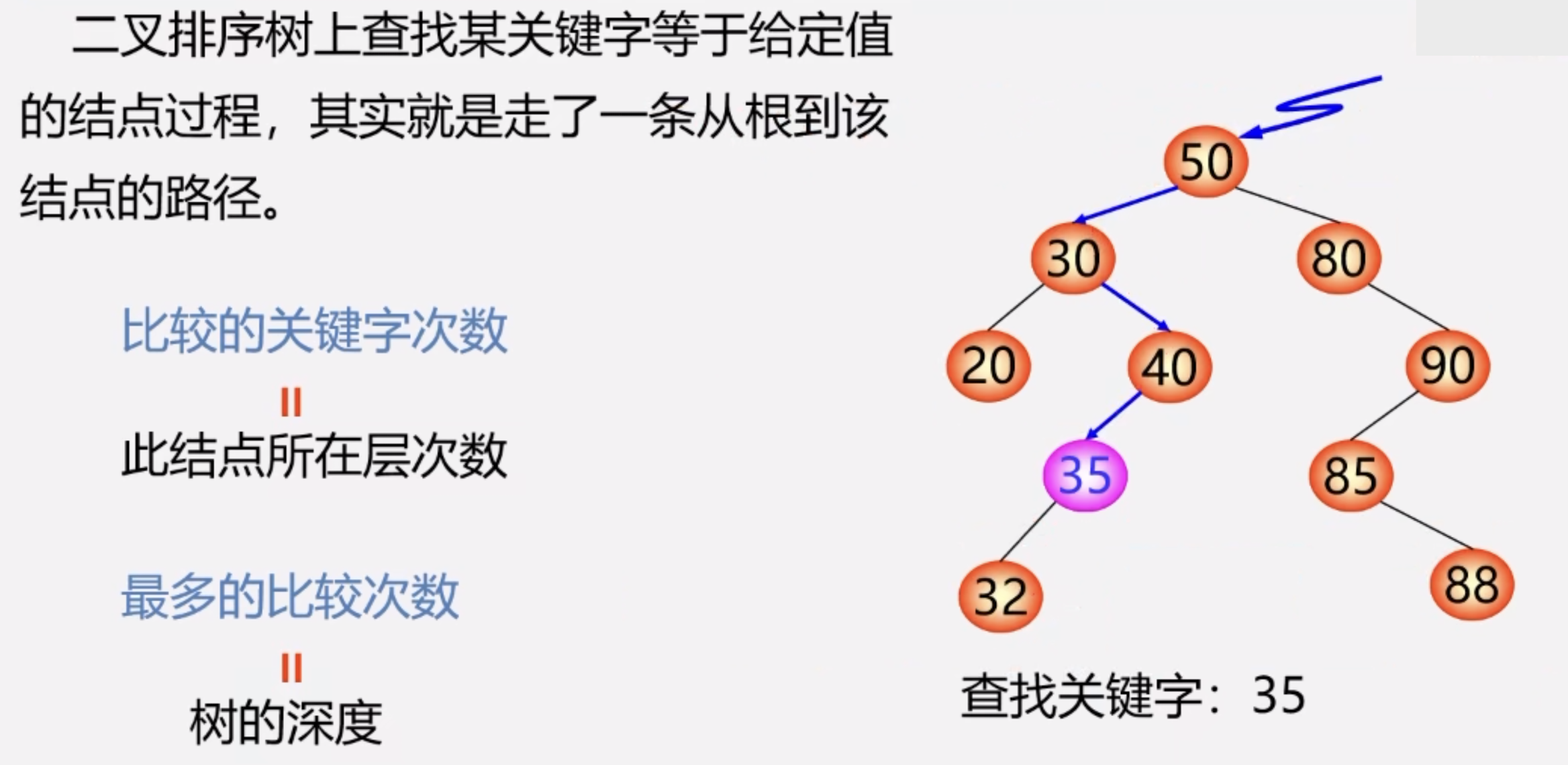
So how to improve the search efficiency of binary sort tree with unbalanced morphology? – > Do "balancing" - balanced binary tree.

Insertion node of binary sort tree

void BSTInsert(BSTree &T, ElemType t)//Inserts an element t into a sorted binary tree
{
    BSTNode *cur = T, *parent = NULL;
    while (cur)//Judge whether the binary tree already contains the keyword
    {
        if (cur->data.key == t.key) return;//If the keyword already exists in the binary tree, it will not be inserted
        parent = cur;
        if (t.key < cur->data.key) cur = cur->lChild;//cur move down
        else cur = cur->RChild;
    }
    BSTNode *p = new BSTNode;//If the binary tree does not contain this keyword, a node is created and inserted into the binary tree
    p->data = t;
    p->lChild = p->RChild = NULL;
    if (parent == NULL) T = p;//The original tree is empty and now it is a tree with one node
    else if (t.key < parent->data.key) parent->lChild = p;//The new node is inserted into the cotyledon of the node referred to by the parent
    else parent->RChild = p;
}

Starting from an empty tree, after a series of insertion operations, a binary sort tree can be generated. An ordered sequence can be obtained by traversing the binary tree in medium order, so the process of generating a sorted binary tree can also be regarded as the sorting process of the sequence. Since all inserted nodes are leaf nodes, there is no need to move other nodes, which is equivalent to inserting nodes in an ordered sequence without moving other records.
Note: the order of keyword sequence is different, and the established sorting binary tree may also be different.

Delete node of binary sort tree

Delete method:

• If the leaf node is deleted, delete it directly
• If the deleted node has only left subtree (or right subtree), replace it with its left subtree (or right subtree)
• If the deleted node has both left and right subtrees
  • Replace the node with the intermediate order precursor node, and then delete the precursor node (the precursor node is the largest node in the left subtree)
    
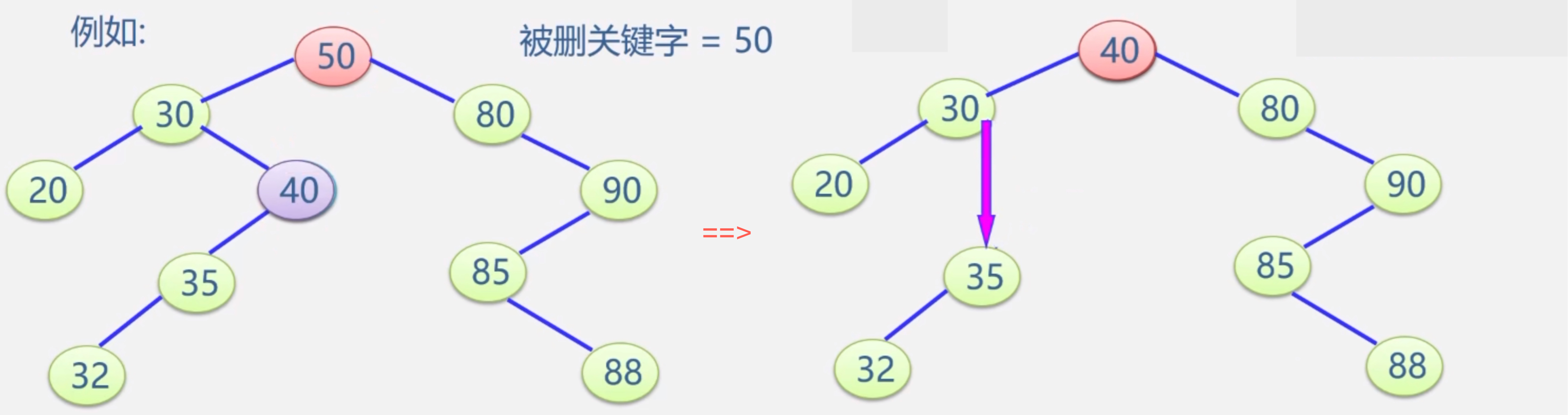
  • You can also replace the node with a middle order successor node, and then delete the successor node (the successor node is the smallest node in the right subtree)

void DeleteNode(BSTNode* &p)//Pass in the node and delete the node from the tree
{
    if (p->RChild == NULL)//This node contains only the left subtree or is a leaf node
    {
        BSTNode *temp = p;
        p = p->lChild;//Replace the node with the left subtree
        delete temp;//Delete this node
    }
    else if (p->lChild == NULL)//This node contains only right subtree or leaf node
    {
        BSTNode *temp = p;
        p = p->RChild;//Replace the node with the right subtree
        delete temp;//Delete this node
    }
    else//The node contains both left and right subtrees
    {
        BSTNode *x = p, *y = p->lChild;
        while (y->RChild)//Find the middle order precursor node of p node
        {
            x = y;
            y = y->RChild;
        }//Finally, y is the precursor node of p node and x is the parent node of Y
        p->data = y->data;//Replace the node with a medium order precursor node
        if (x == p) x->lChild = y->lChild;//If the left child node of p does not have a right subtree, turn the left subtree of y into the left subtree of x
        else x->RChild = y->lChild;//If the left child node of p has a right subtree, turn the left subtree of y into the right subtree of x
        delete y;//Delete the precursor node
    }
}

void BSTDelete(BSTree &T, ElemType t)//Delete node T in binary tree T
{
    if (T == NULL) return;//If the node does not exist in the binary tree, exit the function
    else
    {
        if (t.key == T->data.key) DeleteNode(T);//If the node is found, the node is deleted
        else if (t.key < T->data.key) BSTDelete(T->lChild, t);//Find the node in the left subtree
        else BSTDelete(T->RChild, t);//Find the node in the right subtree
    }
}