1: 01 knapsack problem

 

There are N items and a backpack with a capacity of {V. Each item can only be used once.

The volume of the # i article is # vi and the value is # wi.

Solve which items are loaded into the backpack, so that the total volume of these items does not exceed the backpack capacity, and the total value is the largest.

　　

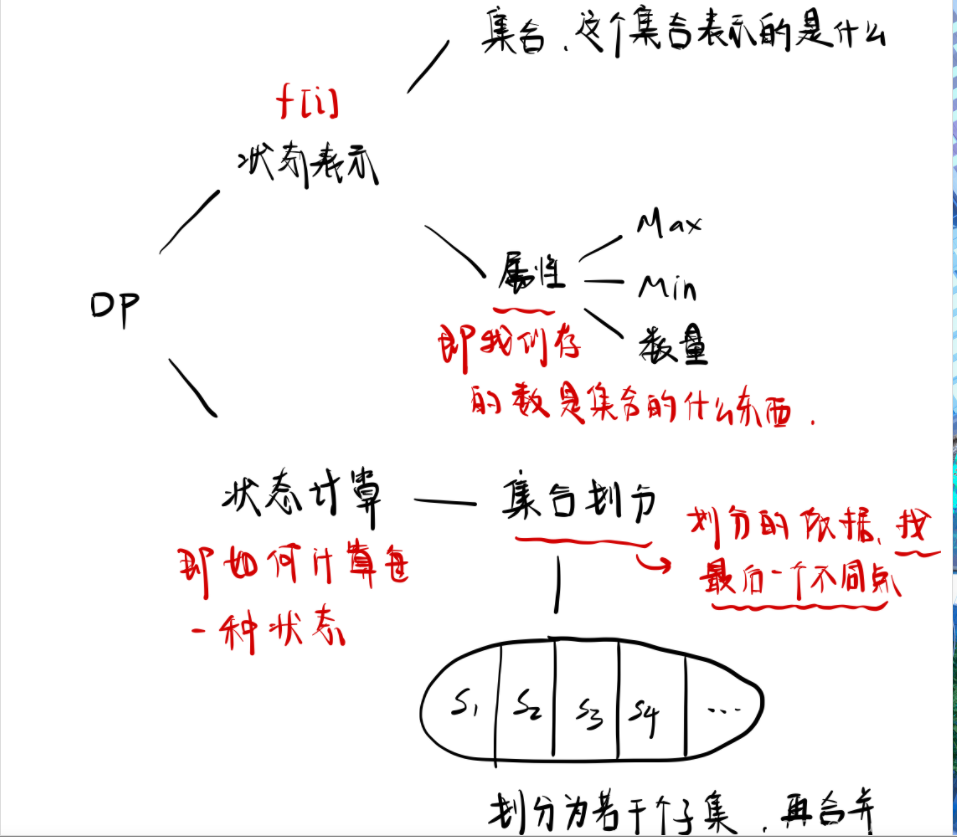
　　1. The idea of transforming f [i] [j] into f [j]: F [i] [j] represents the maximum value obtained when the backpack capacity is j. In one dimension, we lack the dimension of I, and f [j] represents the maximum value obtained when the item has been decided in the previous I round and the backpack capacity is j. Therefore, at the end of the cycle, f [j] represents the maximum value of the final obtained value for which all items have been decided and the backpack capacity is j.

 

　　 2. 01 knapsack state transition equation: F [I, J] = max (f [I - 1, J], f [I - 1, J - v [i]] + w [i]]

One dimensional: F [J] = max (f [J], f [J - v [i] + w [i]]

 

　  3. In the one-dimensional case, the enumeration of knapsack capacity should be in reverse order: in the two-dimensional case, the state f [i] [J] is obtained from the state of the previous round of i - 1, and f [i] [J] and f [i - 1] [J] are independent. After optimization to one dimension, if we are still in positive order, f [smaller volume] is updated to f [larger volume], it is possible that the i - 1 state should have been used, but the i - 1 state is used. Reverse order is to ensure that the status used when updating the current status is the status of the previous round, and ensure that each item has only one or zero times;

 

 1 #include <iostream>
 2 
 3 using namespace std;
 4 
 5 const int N=1e3+10;
 6 int v[N],w[N];
 7 int f[N];
 8 int main()
 9 {
10     int n,m;
11     scanf("%d%d",&n,&m);
12     
13     for(int i=1;i<=n;i++)
14         scanf("%d%d",&v[i],&w[i]);
15     
16     
17     for(int i=1;i<=n;i++)
18     {
19         //If j<v[i]be f[j]==Last round f[j] ,f[j]No need to change 
20         for(int j=m;j>=v[i];j--)            
21             f[j]=max(f[j],f[j-v[i]]+w[i]);
22     }
23     
24     printf("%d\n",f[m]);
25     
26     
27     
28     
29     return 0;
30 }

 

2: Complete knapsack problem

 

There are ， N items and a backpack with a capacity of ， V ， with unlimited items available.

The volume of the ＾ i ＾ article is ＾ vi and the value is ＾ wi.

Solve which items are loaded into the backpack, so that the total volume of these items does not exceed the backpack capacity, and the total value is the largest.

 

　　1. There is no need to reverse the order when enumerating the backpack capacity in one dimension of the complete backpack: the reverse order is to ensure that the state used when updating the current state is the state of the previous round, so as to ensure that each item has only one or zero times; In the complete knapsack, because each item can be taken any number of times, it is no longer required to use the state of the previous round, that is, the items released in this round can be placed later.

 

　　2. Complete knapsack state transition equation: F [I, J - v [i]] = max (f [I - 1] [J], f [I, J - v [i] + w [i]]

One dimensional: F [J] = max (f [J], f [J - v [i]] + w [i])

 

 1 #include <iostream>
 2 
 3 using namespace std;
 4 
 5 const int N=1e3+10;
 6 int v[N],w[N];
 7 int f[N];
 8 int main()
 9 {
10     int n,m;
11     scanf("%d%d",&n,&m);
12     
13     for(int i=1;i<=n;i++)
14         scanf("%d%d",&v[i],&w[i]);
15     
16     for(int i=1;i<=n;i++)
17     {
18         for(int j=v[i];j<=m;j++)f[j]=max(f[j],f[j-v[i]]+w[i]);　　　　//No reverse order, because items can be used unlimited times
19     }
20     
21     printf("%d\n",f[m]);
22     
23     
24     
25     
26     return 0;
27 }

 

 

3: Multiple knapsack problem

 

There are # N items and a backpack with a capacity of # V #.

There are at most ， si ， items of type ， i, each with a volume of ， vi and a value of ， wi.

Solve which items are loaded into the backpack, so that the total volume of items does not exceed the backpack capacity, and the total value is the largest.

　　

 

　　1. Multiple knapsack state transition equation: F [I, J] = max (f [I - 1, J - k * V [i]] + k * w [i]) (k = 0, 1,..., SI)

One dimension: F [J] = max (f [J], f [J - v [i]] + w [i]) (convert binary into 01 knapsack problem)

 

　　2. Binary optimization o (n * V * log SI):

 

　　　　

 

 1 #include <iostream>
 2 
 3 using namespace std;
 4 
 5 const int N=3e7+100;
 6 int v[N],w[N];
 7 int f[N];
 8 int main()
 9 {
10     int n,m;
11     scanf("%d%d",&n,&m);
12     
13     int cnt=0;
14     for(int i=1;i<=n;i++)
15     {
16         int a,b,s;
17         scanf("%d%d%d",&a,&b,&s);
18         
19         int k=1;        //Number in group 
20         while(k<=s)
21         {
22             v[++cnt]=a*k;w[cnt]=b*k;    //Overall volume and value 
23             s-=k;
24             k*=2;        //The number of binary increases in the group 
25         }
26         
27         if(s>0)        //remainder s Separate groups 
28         {
29             v[++cnt]=a*s;w[cnt]=b*s;
30         }    
31     }
32     
33     for(int i=1;i<=cnt;i++)        //Note that the number of enumerations is determined by the number n It becomes the number of groups cnt 
34     {
35         for(int j=m;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);    //01 knapsack 
36     }
37     
38     printf("%d\n",f[m]);
39     
40     
41     
42     
43     return 0;
44 }

 

4: Grouping knapsack problem

There are ， N ， groups of items and a backpack with a capacity of ， V ，.

There are several items in each group. At most one item in the same group can be selected.
The volume of each item is ， vij and the value is ， wij, where ， i ， is the group number and j ， is the number in the group.

Solve which items are loaded into the backpack, so that the total volume of the items does not exceed the capacity of the backpack, and the total value is the largest.

 

　　1. Group knapsack state transition equation: F [I, J] = max (f [I - 1, J], f [I - 1, J - v [i] [k] + w [i] [k]) (k = 1, 2,..., SI)

One dimensional: F [J] = max (f [J], f [J - v [i] [k]] + w [i] [k])

　  2. Enumerating backpack capacity needs to be in reverse order because it is not used infinitely

 

 

 1 #include <iostream>
 2 
 3 using namespace std;
 4 
 5 const int N=2e3;
 6 int s[N],v[N][N],w[N][N];
 7 int f[N];
 8 int main()
 9 {
10     int n,m;
11     scanf("%d%d",&n,&m);
12     
13     for(int i=1;i<=n;i++)
14     {
15         scanf("%d",&s[i]);
16         for(int j=1;j<=s[i];j++)scanf("%d%d",&v[i][j],&w[i][j]);
17     }
18     
19     for(int i=1;i<=n;i++)
20     {
21         for(int j=m;j>=0;j--)　　　　//Reverse order
22         {
23             for(int k=1;k<=s[i];k++)
24             {
25                 if(j>=v[i][k])f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
26             }
27         }
28     }
29     
30     printf("%d\n",f[m]);
31     
32     
33     
34     return 0;
35 }