Binary search routine
I haven't seen hydrology for a long time. Let's write an article on hydrology today...
Recently, I practiced the routine of two-point search to blow a wave
General outline of routine
- Do you know if this question is suitable for two points
1) The target is in a continuous bounded interval (even 0~MAX, this can be achieved basically);
2) Monotonic problem: the problem will tell you that you need to meet certain conditions, such as how many days to complete (set as d) at most, and let you seek the least goal (set as x), then the value f(x) of D must be a monotonic function, so that you can use dichotomy to remove half of the solution space; - Find the monotone function f(x). I generally use count (Num, m) to represent this function;
- Bisection template: bisection of two branches. The side that does not meet the conditions must be reduced (for example, f (x) > d); The satisfied can be set as a new critical value (lo/hi=mid);
- Verify the validity of lo after exiting the loop
The reason is very convoluted. It's easy to understand when it becomes a topic
subject
lc69 sqrt()
Solve sqrt(n), which requires rounding down.
Solve according to the routine:
- If 0 and 1 are excluded, it can be determined that the solution is between (1, n/2); f(x)=x^2, monotonically increasing function (x > 1)
- f(x)=x^2
The rest depends on the code
class Solution {
public int mySqrt(int x) {
/**
0. [0，x]Continuous integer of
1. Monotonicity: f(x)=sqrt(x), monotonically increasing;
2. =mid left
*/
// Special value judgment
if (x == 0) {
return 0;
}
if (x == 1) {
return 1;
}
int lo = 0, hi = x / 2;
while (lo < hi) {
int mid = (hi - lo + 1) / 2 + lo;
if (mid > x / mid) {
hi = mid - 1;
} else {
lo = mid;
}
}
return lo;
}
}
It should be noted that the solution of f(x) should be converted to division, or it will cross the boundary. Don't ask me how I know....
lc1011
This is a standard dichotomous routine problem and an introductory problem. You can practice your hands and get familiar with the routine
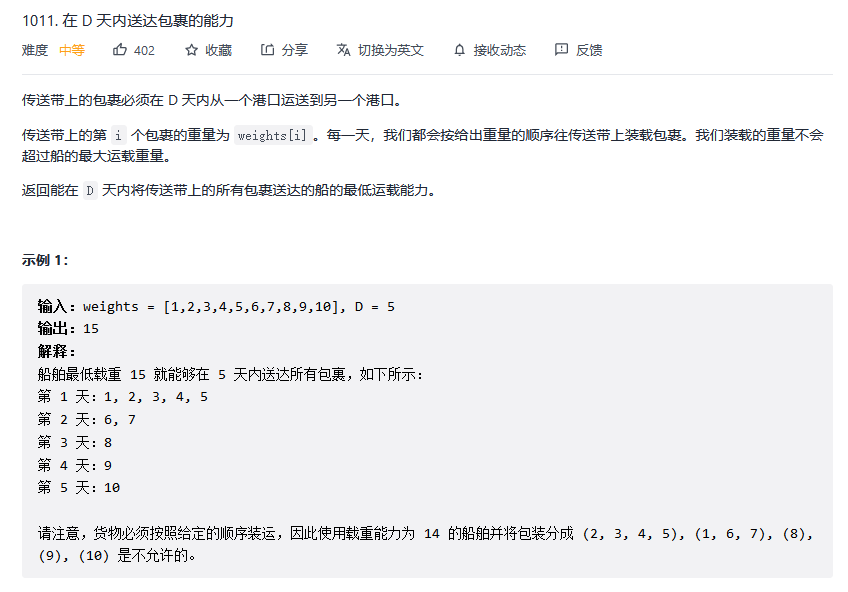
- It can be guessed that if only one cargo is transported a day, it should at least have a carrying capacity of max (Num), otherwise it can not be completed; If you want to complete it in one day, the required carrying capacity is sum (Num), so the target X is bounded, X ∈ [max (Num), sum (Num)]; Although we don't know how to solve f(x), we can be sure that if x increases, the number of days required f(x) will inevitably decrease, otherwise it will increase, which meets the monotonicity and decrement, and it is suitable to use dichotomy;
- The solution of f(x) is very simple. You only need to deliver the goods on another day when cur + num [i] > m;
- Code template, no details, look at the code
class Solution {
public int shipWithinDays(int[] weights, int days) {
int lo = 0, hi = 0;
for (int n:weights) { //lo is the maximum weight, because it must be able to carry; hi is cumulative and can be loaded in one day
lo = Math.max(lo, n);
hi += n;
}
//x: Minimum loading capacity, f(x) number of days required for transportation; Monotone decreasing function
while (lo < hi) {
int m = (hi - lo) / 2 + lo;
int cnt = count(weights, m);
if (cnt > days) {
//Insufficient loading capacity
lo = m + 1;
} else {
//The loading capacity can be appropriately reduced to achieve the optimum
hi = m;
}
}
return lo;
}
private int count(int[] nums, int m) {
int cnt = 1, //At least one day
cur = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] + cur > m) {
cnt++;
cur = 0;
}
cur += nums[i];
}
return cnt;
}
}
Lc410. Maximum value of split array
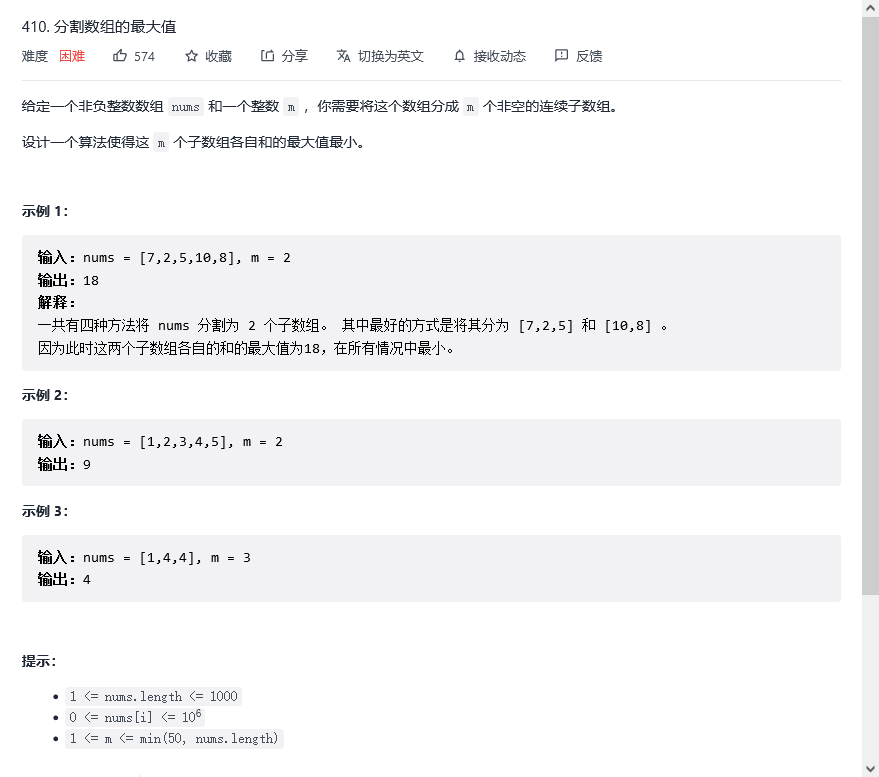Although it is marked as difficult, it is the same as the above question
The difficulty lies in understanding the meaning of the question, but it's really a dog's tongue twister...
You must have a sense of accomplishment after writing a difficult problem so simple~
- Continuous boundedness: in the best case, all array elements are subscripted one by one. At this time, the maximum value is max(nums), so the lower bound is max(nums). In the worst case, it is only reduced to one, and the maximum value is sum(max); It can be expected that if the maximum value of the array is increased, the number of array segmentation will inevitably decrease, and vice versa;
- f(x), which is the segmentation quantity;
- If f (x) > the condition given by the topic, the interval must be abandoned; Otherwise, optimization should continue in this range until lo==hi
class Solution {
public int splitArray(int[] nums, int m) {
/** 2.Dichotomy
Binary scene: find a number in a range of integers;
The basis of binary search: the problem is monotonic
That is, if you want to find element x, the defined search basis is f(x), then you must meet the requirements of F (a) > f(x), a > X
1,Find the minimum value of the maximum value of the split array and set it to x;
2. Function: f(x) is the number of divisions that x can determine
At any position a, if f (a) < f (x), it proves that the number of segmentation is too small, which is less than the best scheme, which will inevitably lead to a > X;
If f(a)=f(x), a==x cannot be determined; (the number of divisions is correct, and the division method is not unique)
If f(a)=f(x)+1, and f(a-1)=f(x) (a-1 is the critical point)
Then: x=a-1
f(x)Monotonic decreasing:
f(x) < m, x > b;
== m, x∈[a, b]
> m, x < a
Requirements: b
*/
int max = 0, sum = 0;
for (int num: nums) {
max = Math.max(max, num);
sum += num;
}
//Left is divided into len segment (f(left)=len), and right is changed into 1 segment (f(right)=1)
int left = max, right = sum;
while (left < right) {
//Currently set a (clip maximum)
int mid = (right - left) / 2 + left;
int splits = split(nums, mid);//Equivalent to f(x)
if (splits < m) {
//The fragment is insufficient and the segmentation degree is not enough, which proves that the maximum value is too small and reduces a
right = mid - 1;
} else {
left = mid;
}
}
return left;
}
//Set the maximum value of a clip to max to see how many clips can be divided
public int split(int[] nums, int max) {
int splits = 1, cur = 0;
for (int n: nums) {
if (cur + n > max) {
//This number cannot be added. This clip ends here
splits++;
cur = 0;
}
cur += n;
}
return splits;
}
}
LCP 12. Xiao Zhang's question brushing plan
This question is the most difficult of these questions. As for the writing of the count() function in f(x), it can also be guessed here that the two most difficult points of the dichotomy problem are:
1) Know that this problem needs to be divided into two points;
2) Write the count() function.
No more questions, the reader will consider for himself
class Solution {
public int minTime(int[] time, int m) {
/**
Find the maximum time x to brush questions, and you can get f(x): number of days to brush questions, monotonic decreasing function
*/
int lo = 0, //All by asking for help
hi = 0; //Finish all the questions by yourself in one day
for (int t: time) {
hi += t;
}
while (lo < hi) {
int mid = (hi - lo) / 2 + lo;
int cnt = count(time, mid);
if (cnt > m) {
//Insufficient time to brush questions
lo = mid + 1;
} else {
hi = mid;
}
}
System.out.println(count(time, 3));
return lo;
}
//t: Current maximum time per day
public int count(int[] nums, int t) {
//In order to minimize the time, record the maximum time spent on each round of problem brushing, and use help to reduce him
int max = 0, cnt = 1, cur = 0;
boolean used = false; //Have you asked for help that day
for (int i = 0; i < nums.length; i++) {
int n = nums[i];
if (n + cur > t) {
if (!used) {
//Use help
used = true;
max = Math.max(max, n);
cur -= max;
} else {
//You can only brush it the next day
cnt++;
cur = 0;
used = false;
max = 0;
}
i--;
continue;
}
max = Math.max(max, n);
cur += n;
}
return cnt;
}
}
My code is rough. Everyone must have a better way to write it...
summary
The two most difficult points of the dichotomy are:
1) Know that this problem needs to be divided into two points;
2) Write the count() function.
The first point is to improve the responsiveness in repeatedly brushing questions. For example, it was difficult for me to think of using and searching sets to solve problems before. After practicing some, now when I see some problems, I will feel that "it's not obvious to use xx", practice make perfect;
The second point depends on the ability of the algorithm, but it is basically a routine, and some conditions may be added.
Attach other exercises and practice by yourself:
lc875: Ke Ke, who likes bananas;
lc1482: minimum number of days required to make m bouquets
lc1552: magnetic force between two balls