Preparatory knowledge

Cross product

1. Introduction of concept

In order to measure the inclination of a straight line in the plane, we introduce the concept of inclination angle. By establishing tan in rectangular coordinate system α = k. We have realized the connection between geometric relations and algebraic relations, which is actually a core of solving geometric problems with computers. Computers do numerical operations, so what you need to do is to express geometric relations with algebraic relations. In space, in order to express the inclination of a plane relative to the space rectangular coordinate system, we use a normal vector perpendicular to the plane to measure (because this is transformed into a problem to describe the inclination of a straight line).

2. Definitions

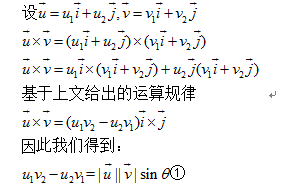
3. Application

(1) Solve triangle (parallelogram) area

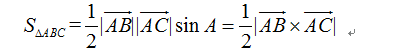
It is more accurate than Helen's formula (reducing the error of open radical)
Based on this conclusion, the calculation formula of n-sided area can also be derived

Strictly speaking, it is also possible to calculate negative values by cross multiplying the area

(2) Point positioning

(3) Polar sorting

Polar angle refers to the angle that establishes polar coordinates and turns counterclockwise with the positive half axis of x axis as the starting edge. The range of this angle is [0,2 π].

Implementation method:

1. Calculate polar angle with cross product (high precision and slow time)

struct point
{
    double x,y;
    point(double x=0, double y=0):x(x), y(y){}
    point operator - (const point &t)const
    {
        return point(x-t.x, y-t.y);
    }//a - b
    double operator *(const point &t)const
    {
        return x*t.x + y*t.y;
    }//a * b
    double operator ^(const point &t)const
    {
        return x*t.y - y*t.x;
    }//a X b
};
double compare(point a,point b,point c)//Calculate polar angle ab ×  ac 
{
    return (b-a)^(c-a);
}
bool cmp(point a,point b)
{
	double f=compare(p[pos],a,b);
	if(f==0) return a.x-p[pos].x<b.x-p[pos].x;
	else if(f>0) return true;
	else return false;
}

If the selected point is not the corner point, it needs to be sorted by quadrant first.

int Quadrant(point a)//Quadrant sorting, note that it contains four axes
{
    if(a.x>0&&a.y>=0)  return 1;
    if(a.x<=0&&a.y>0)  return 2;
    if(a.x<0&&a.y<=0)  return 3;
    if(a.x>=0&&a.y<0)  return 4;
}


bool cmp2(point a,point b)//First quadrant then polar angle
{
    if(Quadrant(a)==Quadrant(b))//The return value is the quadrant
        return cmp(a,b);
    else Quadrant(a)<Quadrant(b);
}

2.atan2 function (fast time and poor accuracy)

The atan2(y,x) function returns the azimuth from the origin to the point (x,y), that is, the included angle with the X axis. It can also be understood as the spokes of the complex x+yi. The unit of the return value is radian. The range of this polar angle here is (− π, π]. The first and second quadrants are positive, and the third and fourth quadrants are negative (the result is positive, indicating the angle of counterclockwise rotation from the X axis, and the result is negative, indicating the angle of clockwise rotation from the X axis). So when we finish sorting from small to large, it is actually the third quadrant < the fourth quadrant < the first quadrant < the second quadrant

struct point
{
	double x,y;
	double angle;
	bool operator <(const point &t)
	{
		return angle<t.angle;
	}
}p[N];
bool cmp(point a,point b)
{
	if(a.angle==b.angle) return a.x<b.x;
	else
	{
		return a.angle<b.angle;
	}
}
for(int i=1;i<=n;i++)
{
	cin>>p[i].x>>p[i].y;
	p[i].angle=atan2(p[i].y,p[i].x);
}
sort(a+1,a+1+n,cmp);

convex hull

1. Definitions

Convex Hull is a concept in computational geometry (graphics).
In a real vector space V, for a given set X, all the vectors containing X convex set The intersection S of is called the convex hull of X. The convex hull of X can be represented by the convex hull of all points (X1,... Xn) in X Convex combination To construct
In two-dimensional Euclidean space, a convex hull can be imagined as a rubber band that just covers all points.
Loosely speaking, given a point set on a two-dimensional plane, a convex hull is a convex polygon formed by connecting the outermost points, which can contain all the points in the point set.

1. For a set D, all the convex combinations of any finite points in D are called the convex hull of D.
2. For a set D, the intersection of all convex sets containing D is called the convex hull of D.
It can be proved that the above two definitions are equivalent

Mathematical definition: let s be any subset of Euclidean space. The minimum convex set containing S is called the convex hull of S and is recorded as conv(S).

concept
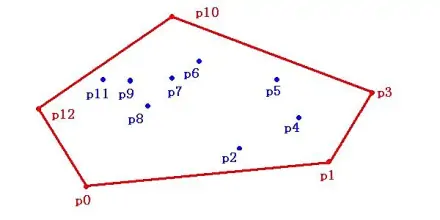
1 the convex hull of point set Q refers to a minimum convex polygon, which satisfies that the points in Q are either on the edge of the polygon or in it. The polygon represented by the red line segment in Figure 1 is the convex hull of the point set Q={p0,p1,... p12}.
2 for a set of points on a plane, find the smallest convex polygon containing all points, which is the convex hull problem. This can be vividly thought of as follows: put some immovable wooden piles on the ground, circle them as tightly as possible with a rope, and they are convex, which is the convex hull.

2. Solution method

Graham's Scan method

Time complexity: O(nlogn)
Idea:
First find a point on the convex hull, and then find the points on the convex hull one by one in a counterclockwise direction from that point. In fact, it is to sort the polar angles, and then query and use them.
Steps:

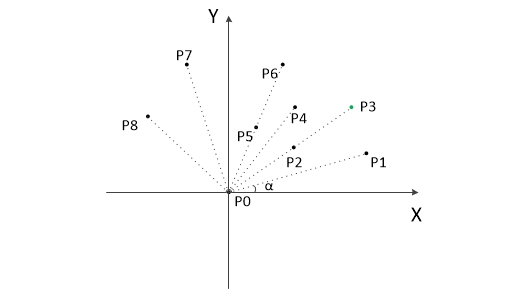
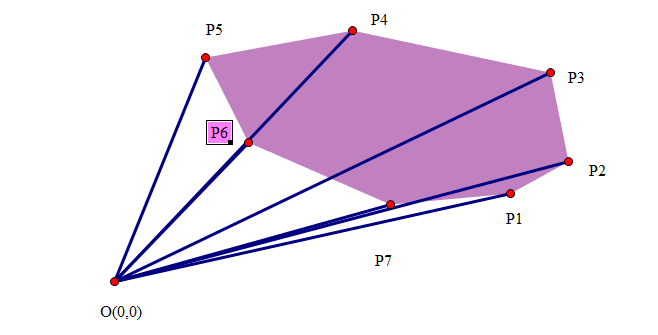
1. If all points are placed in the two-dimensional coordinate system, the point with the smallest ordinate must be the point on the convex hull, as shown in P0 in the figure.
2. Translate the coordinates of all points so that P0 is the origin, as shown in the figure above.
3. Calculate the argument of each point relative to P0 α ， Sort the points from small to large. When α At the same time, those closer to P0 are in front. For example, the results obtained in the above figure are P1, P2, P3, P4, P5, P6, P7 and P8. We can know from geometric knowledge that the first point P1 and the last point P8 in the result must be points on the convex hull.
(the above is the preparation step, and the convex hull is calculated below)
Above, we already know the first point P0 and the second point p1 on the convex hull. We put them in the stack. Now, from the result obtained in step 3, take the point behind P1 as the current point, that is, P2. Next, start looking for the third point:
4. Connect P0 with the point at the top of the stack to get the straight line L. See whether the current point is on the right or left of line L. If it is on the right side of the line, perform step 5; If it is on a straight line or to the left of the straight line, proceed to step 6.
5. If it is on the right, the element at the top of the stack is not a point on the convex hull, and the element at the top of the stack is out of the stack. Perform step 4.
6. The current point is the point on the convex hull. Press it into the stack and perform step 7.
7. Check whether the current point P2 is the last element of the result in step 3. Is the last element. If not, make the point behind P2 the current point and return to step 4.

Template:

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#define N 100005
#define INF 0x3f3f3f3f
#define IO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;

struct point
{
    double x,y;
};

point p[N];
point stackk[N];
int xx,yy;

bool cmp1(point a,point b)
{
    if(a.y == b.y)
        return a.x<b.x;
    else
        return a.y<b.y;
}

double cross(point a,point b,point c)
{
    return (b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}

double dis(point a,point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y)*1.0);
}

bool cmp2(point a,point b)
{
    if(atan2(a.y-yy,a.x-xx) != atan2(b.y-yy,b.x-xx))
        return (atan2(a.y-yy,a.x-xx))<(atan2(b.y-yy,b.x-xx));
    return a.x<b.x;
}

bool cmp(point a,point b)
{
    double m=cross(p[0],a,b);
    if(m>0)
        return 1;
    else if(m==0 && dis(p[0],a)-dis(p[0],b)<=0)
        return 1;
    else
        return 0;
}

int main()
{
    //IO;
    //freopen("D:\\in.txt","r",stdin);
    int n;
    scanf("%d",&n);
    for(int i=0; i<n; i++)
    {
        scanf("%lf%lf",&p[i].x,&p[i].y);
    }
    memset(stackk,0,sizeof(stackk));
    sort(p,p+n,cmp1);
    stackk[0]=p[0];
    xx = stackk[0].x;
    yy = stackk[0].y;
    sort(p+1,p+n,cmp);//Which polar angle to use depends on the specific requirements of the topic
    stackk[1]=p[1];
    int top=1;
    for(int i=2; i<n; i++)
    {
        while(i>=1 && cross(stackk[top-1],stackk[top],p[i])<0)
            top--;
        stackk[++top] = p[i];
    }
    double ans=0;
    for(int i=1; i<=top; i++)
    {
        ans += dis(stackk[i-1],stackk[i]);
    }
    ans += dis(stackk[top],stackk[0]);
    printf("%.2lf",ans);
    return 0;
}

reference material

Computational geometry handout - cross product.
Mathematics: detailed explanation of convex hull algorithm