Enter a   n   that 's ok   m   Column integer matrix, and then enter   q   Operations, each containing five integers   x1,y1,x2,y2,c, where   (x1,y1)   and   (x2,y2)   Represents the upper left and lower right coordinates of a sub matrix.

Each operation adds the value of each element in the selected sub matrix   c.

Please output the matrix after all operations.

Input format

The first line contains integers   n,m,q.

next   n   Rows, each containing   m   An integer representing an integer matrix.

next   q   Rows, each containing   five   Integer   x1,y1,x2,y2,c represents an operation.

Output format

common   n   Line, each line   m   An integer representing the final matrix after all operations are completed.

Data range

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
− 1000 ≤ value of elements in the matrix ≤ 1000

Input example:

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

Output example:

2 3 4 1
4 3 4 1
2 2 2 2

Solution:

A [] [] array is the prefix and array of b [] [] array, then b [] [] is the differential array of a [] []

Original array: a[i][j]

Let's construct a differential array: b[i][j]

This requires a deeper understanding of how to construct a b array

How to construct a b array?

Let's think backwards.

With the same one-dimensional difference, we construct a two-dimensional difference group so that each element of the selected sub matrix in the original two-dimensional array a plus the operation of c can be optimized from the time complexity of O(n*n) to O(1)

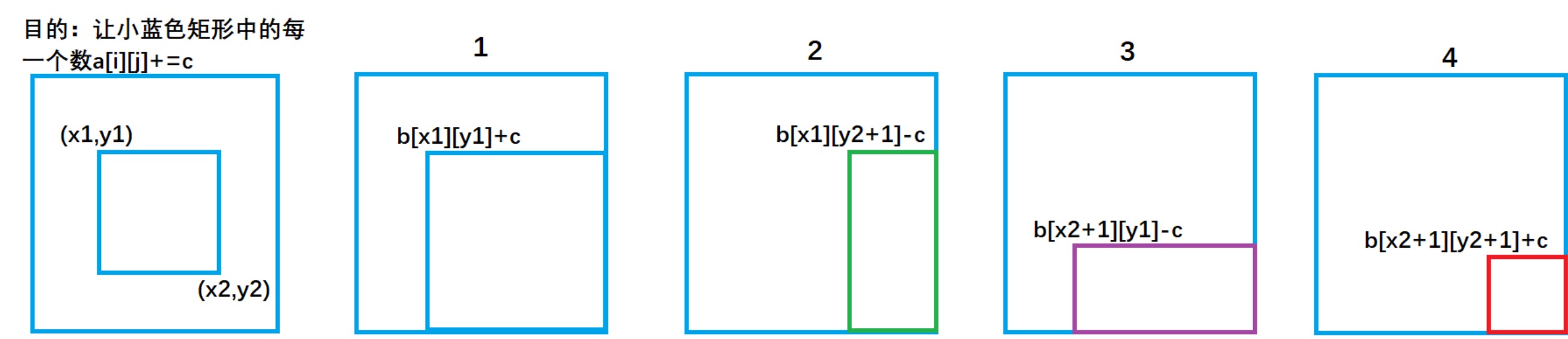
It is known that the selected sub matrix in the original array A is a rectangular area surrounded by (x1,y1) as the upper left corner and (x2,y2) as the upper right corner;

Always remember that array A is the prefix and array of array b. for example, the modification of b[i][j] of array b will affect every number from a[i][j] to array a.

Assuming that we have constructed the b array, we perform the following operations by analogy with one-dimensional difference
Add c to the value of each element in the selected sub matrix

b[x1][y1] + = c;

b[x1,][y2+1] - = c;

b[x2+1][y1] - = c;

b[x2+1][y2+1] + = c;

Each time you perform the above operations on the b array, it is equivalent to:

for(int i=x1;i<=x2;i++)
  for(int j=y1;j<=y2;j++)
    a[i][j]+=c;

We encapsulate the above operations into an insert function:

void insert(int x1,int y1,int x2,int y2,int c)
{     // Performing an insert operation on the b array is equivalent to adding c to the elements between (x1,y1) and (x2,y2) in the a array
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}

We can first assume that array A is empty, then array b is empty at the beginning, but in fact array A is not empty. Therefore, we insert c=a[i][j] every time from the upper left corner of (i,j) to the upper right corner of (i,j) (actually the area of a small square), which is equivalent to adding a[i][j] to the range of (i,j) to (i,j) in the original array a Therefore, the differential b array is successfully constructed by performing n*m insertion operations

The code for building b array is as follows:

  for(int i=1;i<=n;i++)
  {
      for(int j=1;j<=m;j++)
      {
          insert(i,j,i,j,a[i][j]);    // Building differential arrays
      }
  }

Pay attention to understanding ⚠️: Don't confuse the prefix and matrix of a[i][j] and A entered at the beginning. Imagine that A is A virtual matrix. We call the insert function to realize the construction of b array (difference matrix), and the final A matrix is the required one. It is also constructed according to the prefix and sum of two-dimensional array.

Representation of prefix and of two-dimensional array:

b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];  //2D prefix and

Code display:  

#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];

//Encapsulated into a function insert
void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}                                   //Inserting the b array is equivalent to adding c to the elements between (x1,y1) and (x2,y2) in the a array



int main()
{
    int n, m, q;
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            insert(i, j, i, j, a[i][j]);      //Build a differential array and insert c (that is, a[i][j]) one element at a time
        }
    }


    while (q--)
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }


    //The process of outputting an array
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];  //2D prefix and
            printf("%d ", b[i][j]);
        }
        printf("\n"); 
    }

    return 0;
}