Understand data structure binary tree

• Using tree structure can greatly improve efficiency
• Tree structure is the focus of algorithm interview

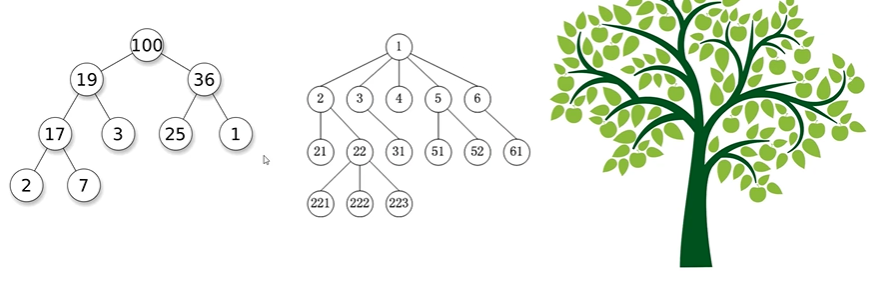
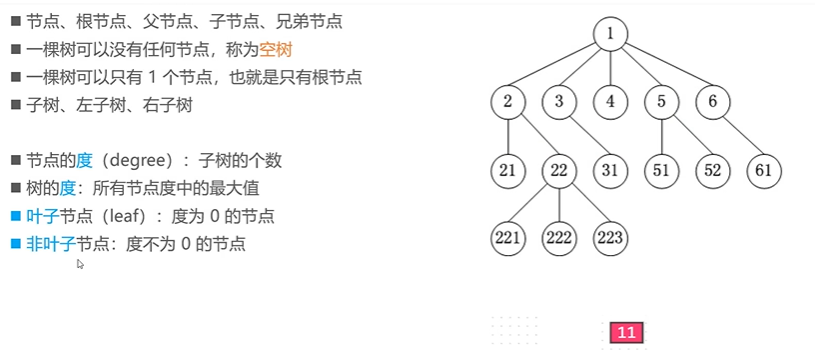
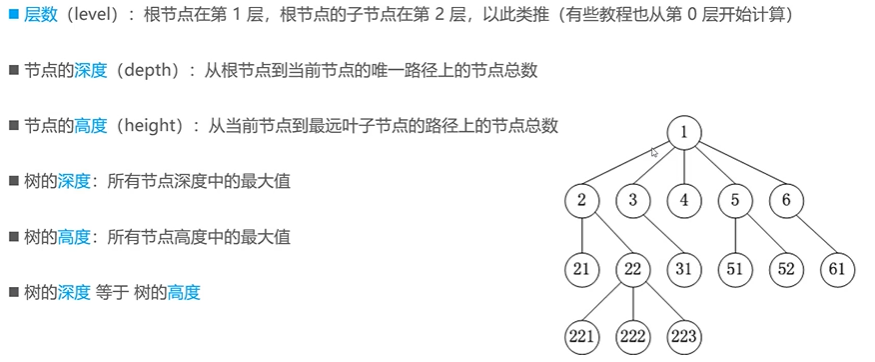
1. Basic concepts of trees

2. Binary tree

2.1 characteristics of binary tree

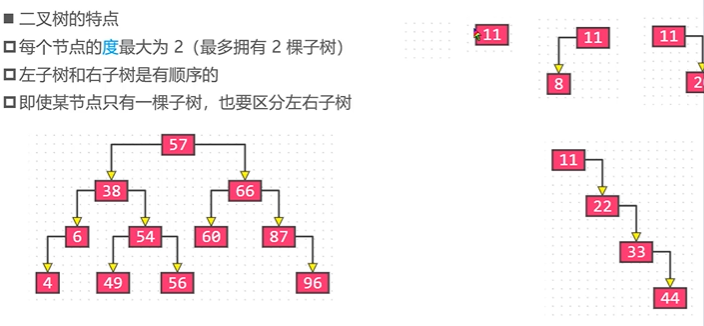
2.2 properties of binary trees

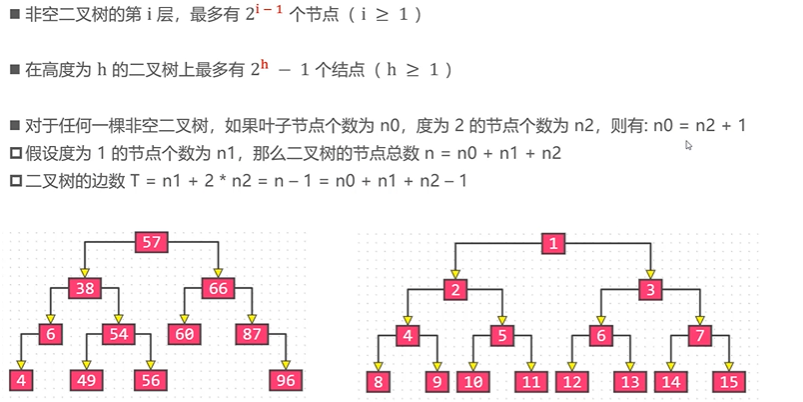
2.3 classification of binary trees

True binary tree

• The degree of all nodes is either 0 or 2, and none is 1.

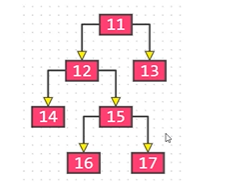
Full binary tree

• The degree of all nodes is either 0 or 2, but all leaf nodes are in the last layer

It can be seen that a full binary tree is a special case of a true binary tree, so a full binary tree must be a true binary tree, and a true binary tree may not be a full binary tree

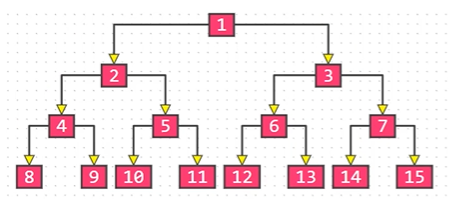
Complete binary tree

• The nodes are numbered from top to bottom, left to right, and all numbers can correspond to the numbers in the full binary tree of the same height

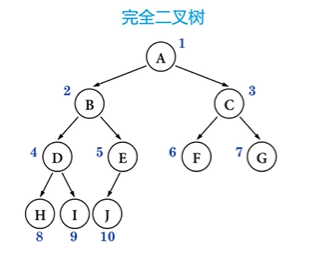
It can be seen from the definition that from the root node to the penultimate layer is a full binary tree, and the leaf node will only appear in the last two layers, and the leaf nodes of the last layer are aligned to the left.

A full binary tree must be a complete binary tree, and a complete binary tree is not necessarily a full binary tree.

Properties of complete binary trees

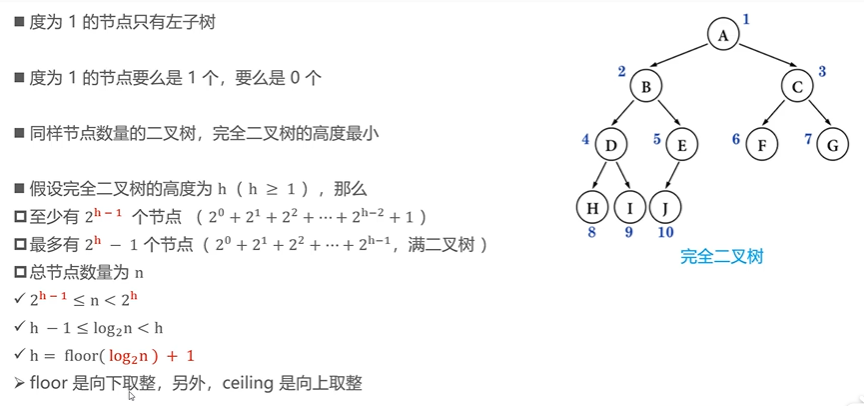
Calculating leaf node and non leaf node of complete binary tree

3. Traversal of binary tree

Traversal of linear data structure:

• Positive order ergodic
• Reverse ergodic

The traversal of binary tree, because there is no index concept, depends on the access order of nodes

• Preorder ergodic
• Middle order ergodic
• Postorder ergodic
• level traversal

3.1 preorder traversal

• Access order: root node, previous order traverses left subtree, previous order traverses right subtree

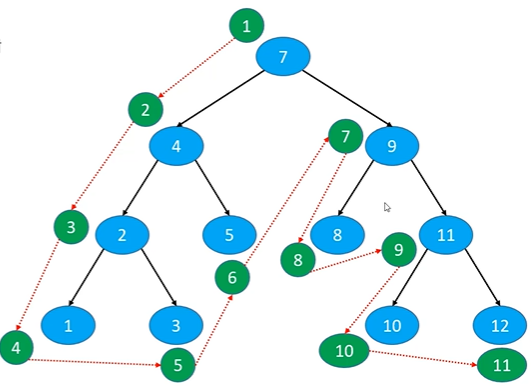
It can be seen that: first access the root node, then the left subtree and then the right subtree

code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    ArrayList<Integer> alist = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        if (root == null) return alist;
        alist.add(root.val);
        preorderTraversal(root.left);
        preorderTraversal(root.right);
        return alist;
    }
}

3.2 middle order traversal

• Middle order traversal left subtree, root node, middle order traversal right subtree

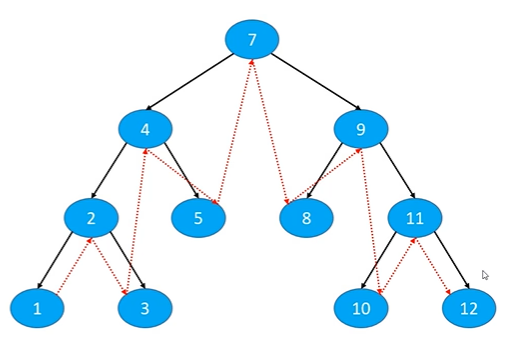
It can be seen that first traverse the left subtree, then follow the node, and then the right subtree

If the tree is a binary search tree, the traversal result is an ascending structure

code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    ArrayList<Integer> alist = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        if (root == null) return alist;
        inorderTraversal(root.left);
        alist.add(root.val);
        inorderTraversal(root.right);
        return alist;
    }
}

3.3 subsequent traversal

• Traversing the left subtree and the right subtree, following the nodes

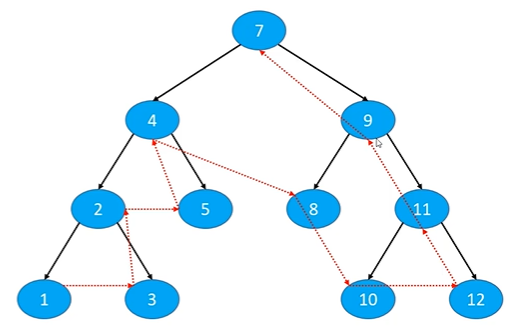
code

class Solution {
    ArrayList<Integer> alist = new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) {
        if (root == null) return alist;
        postorderTraversal(root.left);
        postorderTraversal(root.right);
        alist.add(root.val);
        return alist;
    }
}

3.4 sequence traversal

• Access each node from top to bottom, left to right

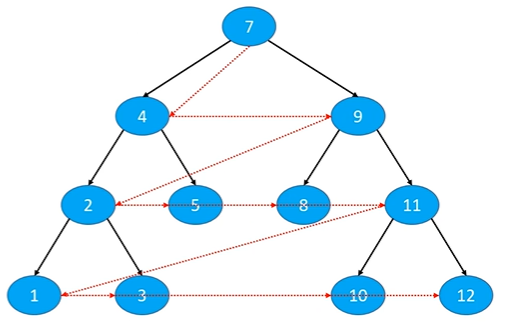
It can be seen that the 4 nodes are accessed first, and when the next layer accesses, the 4 subtrees are accessed first. Here is the meaning of first in, first out. All data structures of queues are considered to be implemented

Implementation ideas:

1. Team root
2. Loop through the following until the queue is empty
   1. Leave team leader node A to visit
   2. Queue the left child of A
   3. Queue the right child of A

code:

[
  [3],
  [9,20],
  [15,7]
]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    List<List<Integer>> resList = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        if (root == null) return resList;
        Queue<TreeNode> queue = new LinkedList<>();
        int levelSize = 1;
        // Root join the team
        queue.offer(root);
        List<Integer> list = new ArrayList<>();
        while (! queue.isEmpty()){
            // Out of the team
            TreeNode node = queue.poll();
            list.add(node.val);
            levelSize--;

            if (node.left != null){
                queue.offer(node.left);
            }
            if (node.right != null){
                queue.offer(node.right);
            }
            if (levelSize == 0){
                resList.add(list);
                levelSize = queue.size();
                list = new ArrayList<>();
            }

        }
        return resList;
    }
}

4. Application of traversal

• Preorder traversal: the display of tree structure
• Middle order traversal: binary search trees are arranged in order after traversal
• Post order traversal: applicable to some operations of first child and then parent
• Level traversal, calculate the height of binary tree, and judge whether it is a complete binary tree

4.1 reconstruction of binary tree based on traversal results

• Preorder traversal + middle order traversal
• Post order traversal + middle order traversal

According to the above two combinations, a unique binary tree can be reconstructed

It can be located to the root node according to the traversal of pre order or post order. According to the root node, we can know the left and right subtrees in the middle order traversal. Continue to find the root node of the subtree in the pre or post order. In this way, the unique binary tree can be reconstructed.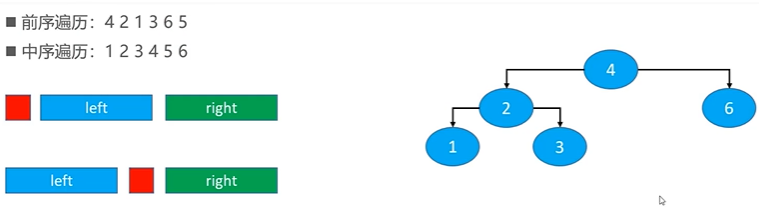

• If the binary tree is a true binary tree, the reconstruction result is unique, otherwise the result is not unique

4.2 forerunner and successor

Note that the precursor and successor of a tree are not the same as its linear structure.

• The predecessor node is the former of the middle order traversal
• The successor node is the next one traversed by the middle order

If it is a binary search tree, the predecessor node is the one smaller than it.

Precursor node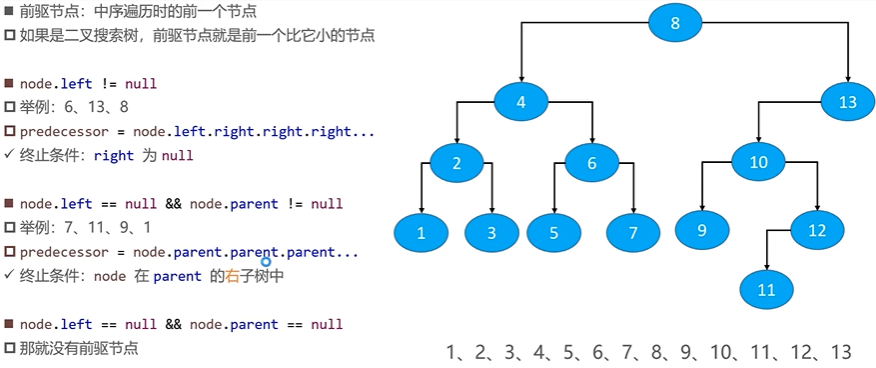

code implementation

private Node<E> predecessor(Node<E> node){
    if (node == null) return null;
    Node<E> p = node.left;
    //The predecessor node is in the left subtree
    if (node.left != null){
        while (p.right != null){
            p = p.right;
        }
        return p;
    }
    // Looking up from the parent node
    while (node.parent != null && node == node.parent.left){
        node = node.parent;
    }
    return node.parent;
}

Successor node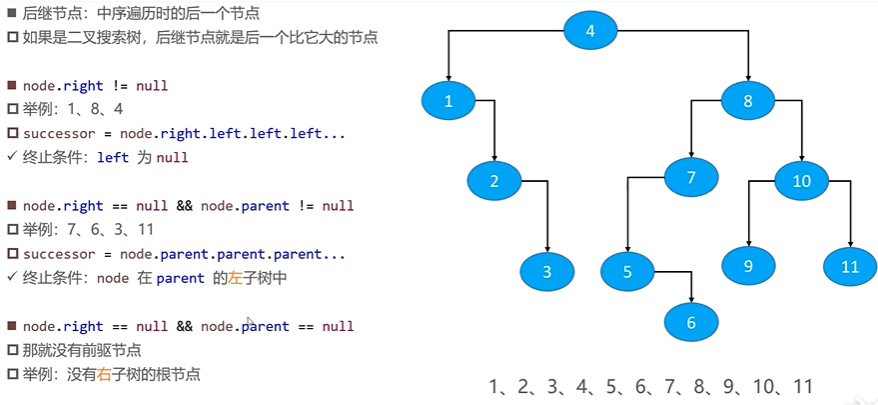

Implementation code

/**
 * Subsequent
 * @param node
 * @return
 */
private Node<E> succssor(Node<E> node){
    if (node == null) return null;
    Node<E> s = node.right;
    if (node.right != null){
        while (s.left != null){
            s = s.left;
        }
        return s;
    }
    while (node.parent != null && node == node.parent.right){
        node = node.parent;
    }
    return node.parent;
}

5. Practice

1. Calculate the height of binary tree

Method 1: recursion

Recursion: the method is to calculate the maximum height, then the maximum height of this node is equal to the maximum height of the child node + 1;

public class Solution {
    public int TreeDepth(TreeNode root) {
        if (root == null) return 0;
        return 1 + Math.max(TreeDepth(root.left), TreeDepth(root.right));
    }
}

Method 2: iteration, hierarchical traversal

Because the depth is calculated, a variable is needed to record the depth; in addition, a variable is needed to record the number of each layer. However, if the number of each layer is reduced to 0, the depth is increased by 1, and then the number of each layer is updated.

public class Solution {
    public int TreeDepth(TreeNode root) {
        if (root == null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int height = 0;
        int levelSize = 1;
        while (!queue.isEmpty()){
            TreeNode node = queue.poll();
            levelSize--;
            if (node.left != null){
                queue.offer(node.left);
            }
            if (node.right != null){
                queue.offer(node.right);
            }
            if (levelSize == 0){
                height++;
                levelSize = queue.size();
            }
        }
        return height;
        
    }
}

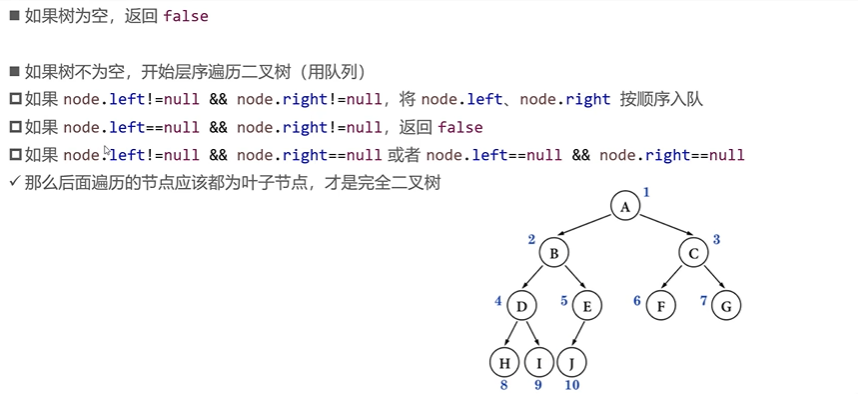
2. Judge complete binary tree

Judgment logic:

code:

/**
 * No matter what the use of hierarchical traversal is, it is necessary to write out the logic first, and then proceed to the next step according to the requirements
 * @return
 */
public boolean isComplete(){
    if (root == null) return false;
    Queue<Node> queue = new LinkedList<>();
    queue.offer(root);
    boolean leaf = false;
    while (! queue.isEmpty()){
        Node node = queue.poll();
        //( node.left != null || node.right != null): judge whether it is a child node
        if (leaf && (node.left != null || node.right != null)) return false;

        if (node.left != null){
            queue.offer(node.left);
        }else if (node.right != null){
            return false;
        }

        if (node.right != null){
            queue.offer(node.right);
        }else {
            //In this case, the nodes to be traversed later must be leaf nodes
            //It's a clever sign
            leaf = true;
        }
    }
    return true;
}

3. Flip binary tree

Ideas:

It can traverse every node, and then exchange left and right subtrees. In essence, it is ergodic, and all four ergodic methods can be implemented.

code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
//level traversal 
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return root;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            TreeNode node = queue.poll();
            TreeNode temp = node.left;
            node.left = node.right;
            node.right = temp;

            if (node.left!=null){
                queue.offer(node.left);
            }
            if (node.right != null){
                queue.offer(node.right);
            }
        }
        return root;
    }
}
//Preorder ergodic
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return root;
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;        
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

Note: only for learning and communication