Recently, I came across kmp algorithm in question brushing. After further learning online class on station b, I have a deeper understanding of this

For the string ss with length of mm, the prefix function \ PI (i)(0 \ Leq I < m) π (i)(0 ≤ I < m) represents the length of the longest equal true prefix and true suffix of the substring s[0:i]s[0:i] of ss. In particular, if there is no qualified pre suffix, then \ PI (i)=0 π (i)=0. The true prefix and true suffix are defined as prefixes and suffixes that are not equal to their own.

Let's take an example to illustrate: the prefix function values of string aabaabaabaaab are 0,1,0,1,2,2,30,1,0,1,2,2,3.

\pi(0)=0 π (0) = 0, because aa has no true prefix and true suffix, it is specified as 00 (it can be found that for any string \ pi(0)=0 π (0) = 0 must be true);

\pi(1) = 1 π (1) = 1, because the longest pair of equal true pre suffixes of aaaa is aa and the length is 11;

\pi(2) = 0 π (2) = 0, because aabaab has no corresponding true prefix and true suffix, which is 00 according to the regulations;

\pi(3) = 1 π (3) = 1, because the longest pair of equal true pre suffixes of aabaaaba is aa and the length is 11;

\pi(4) = 2 π (4) = 2, because the longest pair of equal true pre suffixes of aabaaaabaa is aaaa and the length is 22;

\pi(5) = 2 π (5) = 2, because the longest pair of equal true pre suffixes of aabaaaabaaaa is aaaa and the length is 22;

\pi(6) = 3 π (6) = 3, because the longest pair of equal true pre suffixes of aabaaaabaabaaaaab is aabaab, with a length of 33.

With the prefix function, we can quickly calculate every occurrence of the pattern string in the main string

 

 

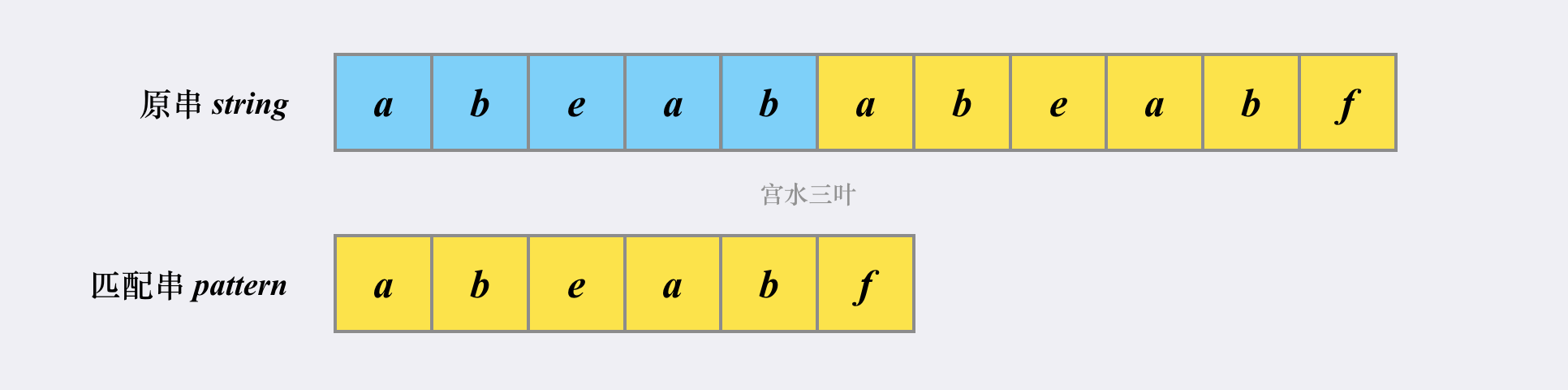
Here, I'll explain it with the picture of a big man

Let's first look at how to match if KMP is not used (without substring function).

First, there is a pointer to the current matching position in the "original string" and "matching string" respectively.

The "starting point" of the first match is the first character a. Obviously, the following abeab matches, and the two pointers will move to the right at the same time (black mark).

In the part where abeab can be matched, there is no difference between "naive matching" and "KMP"

Author: AC_OIer
Link: https://leetcode-cn.com/problems/implement-strstr/solution/shua-chuan-lc-shuang-bai-po-su-jie-fa-km-tb86/
Source: LeetCode

The reason why kmp algorithm can simplify the operation is its next array. The next array helps you skip many incorrect options and make the operation easier. Next, we use a line of simple code to solve the next array

void getvoid GetNext(int next[],int length,char *s){

void GetNext(char*s,int length,int next[]) {     next[0]=0;     int i=1,j=0;

//First, we initialize J to be equal to zero, where j represents the lower flag of the last number of the prefix of the pattern string, and also represents the same maximum value of the pre suffix. J table seems to be the position indicated by the last subscript of the suffix

    for(i=1;i<length;i++){         while(j>0 && s[i]!=s[j]){             j=next[j-1];　　　　　　//When they are not equal, use the while loop to backtrack         }         if(s[i]==s[j])　　　　　　　//Add j forward when equal         {             j++;         }         next[i]=j;　　　　　　　　//Update the next array. Here, use next[i]=j     } }      int strStr(char* haystack, char* needle) {     int numssize1=strlen(haystack);     int numssize2=strlen(needle);//First get the length of the pattern string and the target string          if(numssize2==0){         return 0;//If the length of the pattern string is zero, it returns zero, which conforms to the definition of "0" in c language???     }     int next[numssize2];     int j=0,i=0;     GetNext(needle,numssize2, next);//Initialize next array     for(i=0;i<numssize1;i++)     {         while(j>0 && haystack[i]!=needle[j]){   //i and j at this time have different meanings from i and j above. Beginners often make mistakes (including me, of course)             j=next[j-1];                                  //If the matching is unsuccessful, it will be traced back. It is in this step that the operation is simplified. Why? Since the array subscript can be added to j, it means that the first few numbers must be the same as the first j characters of the target string                                                               //If the matching is successful, then I does not move. We just need to compare the first need [next [J-1] + 1] and haystack[i], in other words,                                                               //At this time, the matching process is reset, and only the first next[j-1] numbers in haystack are used, instead of the previous j numbers,                                                              //On the contrary, if the matching fails at this time, the while loop will keep backtracking until 0 (note that j still points to need at this time)         }         if(haystack[i]==needle[j]){             j++;                                         //At this time, if the match is successful, j++         }         if(j==numssize2)                      //It shows that after taking the postgraduate entrance examination, J success has come to the end. Pay attention! At this time, j is j-1 at the last time, and + 1 after equality, that is, next[j] has crossed the boundary at this time, and we have not used knowledge. After that         return (i-numssize2+1);              //If you reuse it, you still have to be careful                                                           //At this time, i has pointed to the corresponding position + numsize. According to the meaning of the question, we add 1     }     return -1;                                   //If the function does not return at the previous exit after all traversals, indicating that there is no place in the target stream that matches the pattern string, then - 1 is returned }

What I want to say,All the points that should be paid attention to have been,Write it in the notes,I hope it can help you!!!