catalogue

1, Basic understanding of red black tree

(1) Understanding of the basic definition of red black tree

(2) Understanding that red black tree is "approximate equilibrium"

1. Remove the red node from the red black tree and analyze the height of the red black tree containing the black node

2. Add back the red node and analyze the height change

(3) Comparison between red black tree and AVL tree:

2, Analysis on the basic idea of realizing red black tree

(1) Understand the operation of rotate left and rotate right

(2) Balance adjustment of insertion operation

Case 1: if the concerned node is a, its uncle node d is red

Case 2: if the concerned node is a, its uncle node d is black, and the concerned node a is the right child node of its parent node b

Case 3: if the concerned node is a, its uncle node d is black, and the concerned node a is the left child node of its parent node b

The specific codes above are as follows:

(3) Balance adjustment for delete operation

1. Preliminary adjustment for deleted nodes

Case 1: if the node to be deleted is a, it has only one child node b

If a has two non child nodes of c, it is the case that a wants to delete its two child nodes

Case 3: if node a is to be deleted, it has two non empty child nodes, and the successor node of node a is not a right child node

2. Make secondary adjustment for concerned nodes

Case 1: if the node of interest is a, its brother node c is red

Case 2: if the node of interest is a, its brother node c is black, and the left and right child nodes d and e of node c are black

Case 3: if the node of interest is a, its brother node c is black, the left child node d of c is red, and the right child node e of c is black

Case 4: if the brother node c of node a is black and the right child node of c is red

The above specific codes can be seen:

References and links:

1, Basic understanding of red black tree

(1) Understanding of the basic definition of red black tree

The English of red black tree is "red black tree", which is called R-B Tree for short. It is a kind of relaxed balanced binary search tree

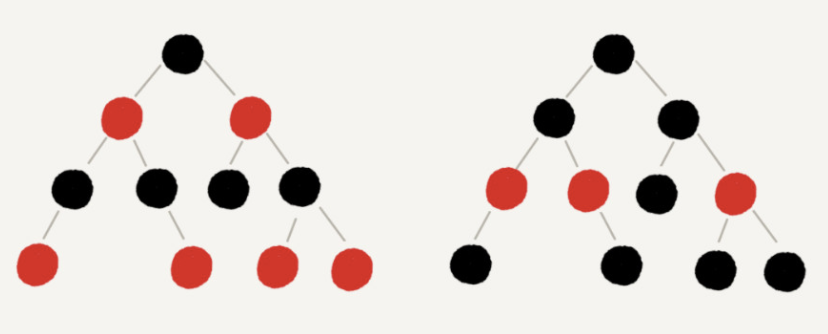
The nodes in the red black tree are marked as black and red. In addition, a red black tree also needs to meet the following requirements:

• The root node is black;
• Each leaf node is a black empty node (NIL), that is, the leaf node does not store data (the black and empty leaf nodes are omitted in the figure);
• Any adjacent nodes cannot be red at the same time, that is, red nodes are separated by black nodes;
• Each node, all paths from the node to its leaf node, contain the same number of black nodes;

(2) Understanding that red black tree is "approximate equilibrium"

The original intention of balancing binary search tree is to solve the problem of performance degradation caused by dynamic update of binary search tree. Therefore, the meaning of "balance" can be equivalent to no degradation of performance. "Approximate balance" is equivalent to that the performance will not degrade too seriously.

The height of an extremely balanced binary tree (full binary tree or complete binary tree) is about log2n, so if you want to prove that the red black tree is approximately balanced, you only need to analyze whether the height of the red black tree is stably approaching log2n.

1. Remove the red node from the red black tree and analyze the height of the red black tree containing the black node

After the red node is deleted, some nodes have no parent node. They will directly take the grandfather node (the parent node of the parent node) of these nodes as the parent node. Therefore, the previous binary tree has become a quadtree.

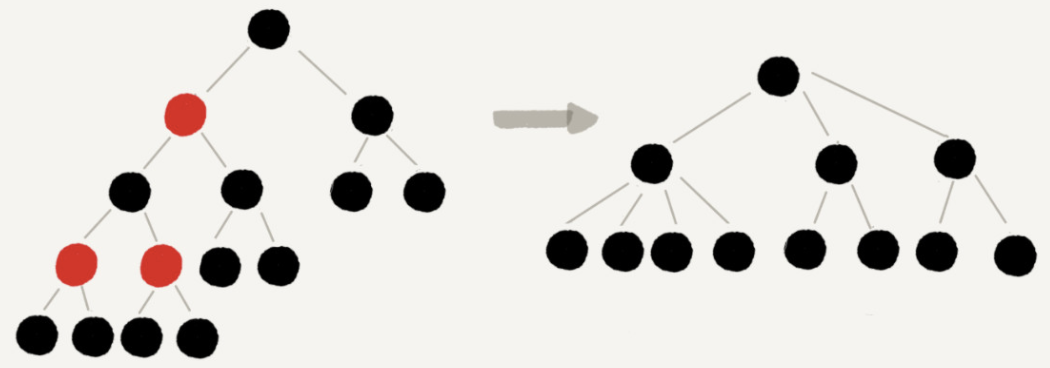
Take out some nodes from the quadtree and put them at the leaf node, and the quadtree becomes a complete binary tree. Therefore, the height of a quadtree with only black nodes is smaller than that of a complete binary tree with the same number of nodes.

The height of the complete binary tree is similar to log2n. The height of the quad "black tree" here is lower than that of the complete binary tree, so the height of the "black tree" without red nodes will not exceed log2n.

2. Add back the red node and analyze the height change

In the red black tree, red nodes cannot be adjacent, that is, if there is a red node, there must be at least one black node to separate it from other red nodes.

The path containing the most black nodes in the red black tree will not exceed log2n, so after adding red nodes, the longest path will not exceed 2log2n, that is, the height of the red black tree is approximately 2log2n.

Therefore, the height of the red black tree is only twice that of the highly balanced AVL tree (log2n), and the performance does not decline much. The result derived in this way is not accurate enough. In fact, the performance of red black tree is better.

(3) Comparison between red black tree and AVL tree:

• Although the time complexity of AVL tree is better than that of red black tree, the cpu is too fast for today's computers, and the performance difference can be ignored
• The insertion and deletion of red black tree is easier to control than AVL tree
• The overall performance of red black tree is slightly better than that of AVL tree (the rotation of red black tree is less than that of AVL tree)

2, Analysis on the basic idea of realizing red black tree

The balance process of the red black tree is very similar to the restoration of the Rubik's cube. The general process is: what kind of node arrangement we encounter, we will adjust it accordingly. As long as these fixed adjustment rules are followed, an unbalanced red black tree can be adjusted to balanced.

As mentioned above, among the four basic requirements that a qualified red black tree needs to meet, the third and fourth requirements may be destroyed in the process of inserting and deleting nodes, and "balance adjustment" is actually to restore the damaged third and fourth points. The specific analysis is as follows:

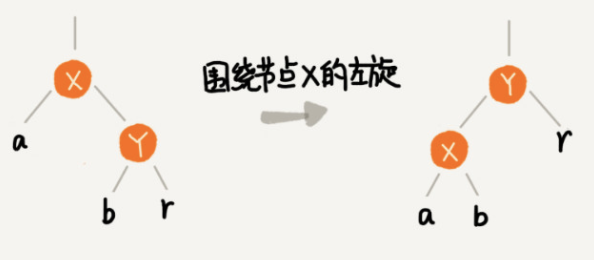
(1) Understand the operation of rotate left and rotate right

Left rotation is the left rotation around a node. A, b and r in the figure represent subtrees and can be empty.

Specific code implementation:

   

     

      

     
     

      

       /**
      
     

     

      

     
     

      

            * Function Description: left-hand and right-hand need to be balanced
      
     

     

      

     
     

      

            *
      
     

     

      

     
     

      

            * @author yanfengzhang
      
     

     

      

     
     

      

            * @date 2020-05-27 14:57
      
     

     

      

     
     

      

            */
      
     

     

      

     
     

      
    
       private void rotateLeft(Entry<K, V> p) {
      
     

     

      

     
     

      
        
       if (p != 
       null) {
      
     

     

      

     
     

      
            
       /*Get the right child node of the root node */
      
     

     

      

     
     

      

                   Entry<K, V> r = p.right;
      
     

     

      

     
     

      
            
       /*Assign a value to the left node of the right child node of the root node*/
      
     

     

      

     
     

      

                   p.right = r.left;
      
     

     

      

     
     

      
            
       if (r.left != 
       null)
      
     

     

      

     
     

      
                
       /*Assign the value of the root node to the currently disconnected following node*/ {
      
     

     

      

     
     

      

                       r.left.parent = p;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      
            
       /*r In the future, it will become a new root node. p.parent is the root, making it a new following node */
      
     

     

      

     
     

      

                   r.parent = p.parent;
      
     

     

      

     
     

      
            
       if (p.parent == 
       null) {
      
     

     

      

     
     

      

                       root = r;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      
            
       /*If p is a left child, let him still be a left child*/
      
     

     

      

     
     

      
            
       else 
       if (p.parent.left == p) {
      
     

     

      

     
     

      

                       p.parent.left = r;
      
     

     

      

     
     

      

                   } 
       else {
      
     

     

      

     
     

      

                       p.parent.right = r;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      
            
       /*Finally, the current exchanged follow-up value*/
      
     

     

      

     
     

      

                   r.left = p;
      
     

     

      

     
     

      

                   p.parent = r;
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      

           }
      
     
   

Right rotation is the right rotation around a node. A, b and r in the figure represent subtrees and can be empty.

Specific code implementation:

   

     

      

     
     

      
    
       /**
      
     

     

      

     
     

      

            * Function Description: right hand code
      
     

     

      

     
     

      

            *
      
     

     

      

     
     

      

            * @author yanfengzhang
      
     

     

      

     
     

      

            * @date 2020-05-27 14:58
      
     

     

      

     
     

      

            */
      
     

     

      

     
     

      
    
       private void rotateRight(Entry<K, V> p) {
      
     

     

      

     
     

      
        
       if (p != 
       null) {
      
     

     

      

     
     

      

                   Entry<K, V> l = p.left;
      
     

     

      

     
     

      

                   p.left = l.right;
      
     

     

      

     
     

      
            
       if (l.right != 
       null) {
      
     

     

      

     
     

      

                       l.right.parent = p;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      

                   l.parent = p.parent;
      
     

     

      

     
     

      
            
       if (p.parent == 
       null) {
      
     

     

      

     
     

      

                       root = l;
      
     

     

      

     
     

      

                   } 
       else 
       if (p.parent.right == p) {
      
     

     

      

     
     

      

                       p.parent.right = l;
      
     

     

      

     
     

      

                   } 
       else {
      
     

     

      

     
     

      

                       p.parent.left = l;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      

                   l.right = p;
      
     

     

      

     
     

      

                   p.parent = l;
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      

           }
      
     
   

(2) Balance adjustment of insertion operation

The red black tree stipulates that the inserted node must be red. Moreover, the newly inserted nodes in the binary search tree are placed on the leaf nodes.

There are two special cases about the balance adjustment of the insertion operation:

• If the parent node of the inserted node is black, we don't have to do anything. It still meets the definition of red black tree.
• If the inserted node is the root node, we can directly change its color and turn it into black.

In addition, other situations will violate the definition of red black tree and need to be adjusted. The adjustment process includes two basic operations: left and right rotation and color change.

The balance adjustment process of red black tree is an iterative process. The node being processed is called the concerned node. The nodes of interest will constantly change with the continuous iterative processing. The first node of interest is the newly inserted node. After a new node is inserted, if the balance of the red black tree is broken, there are generally three situations:

Note: we only need to constantly adjust according to the characteristics of each situation, so that the red black tree can continue to meet the definition, that is, to maintain balance. In order to simplify the description, the brother node of the parent node is called the uncle node, and the parent node of the parent node is called the grandfather node.

Case 1: if the concerned node is a, its uncle node d is red

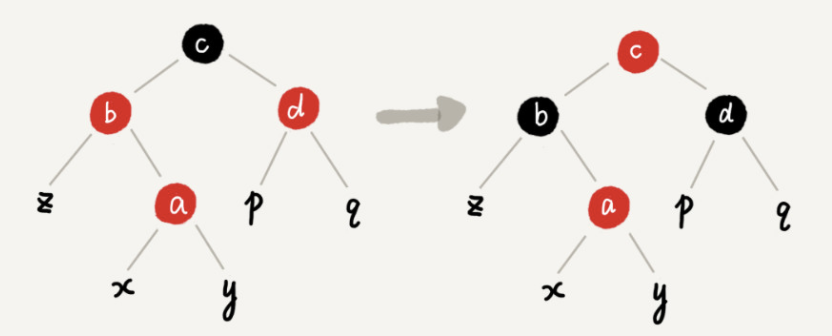
The specific operations are as follows: set the color of parent node b and uncle node d of node a to black; Set the color of the grandfather node c of the node of interest a to red; The concerned node becomes the grandfather node c of a; Skip to case 2 or case 3.

Case 2: if the concerned node is a, its uncle node d is black, and the concerned node a is the right child node of its parent node b

The specific operations are as follows: the concerned node becomes the parent node b of node a; Rotate left around the new focus node b; Skip to case three.

Case 3: if the concerned node is a, its uncle node d is black, and the concerned node a is the left child node of its parent node b

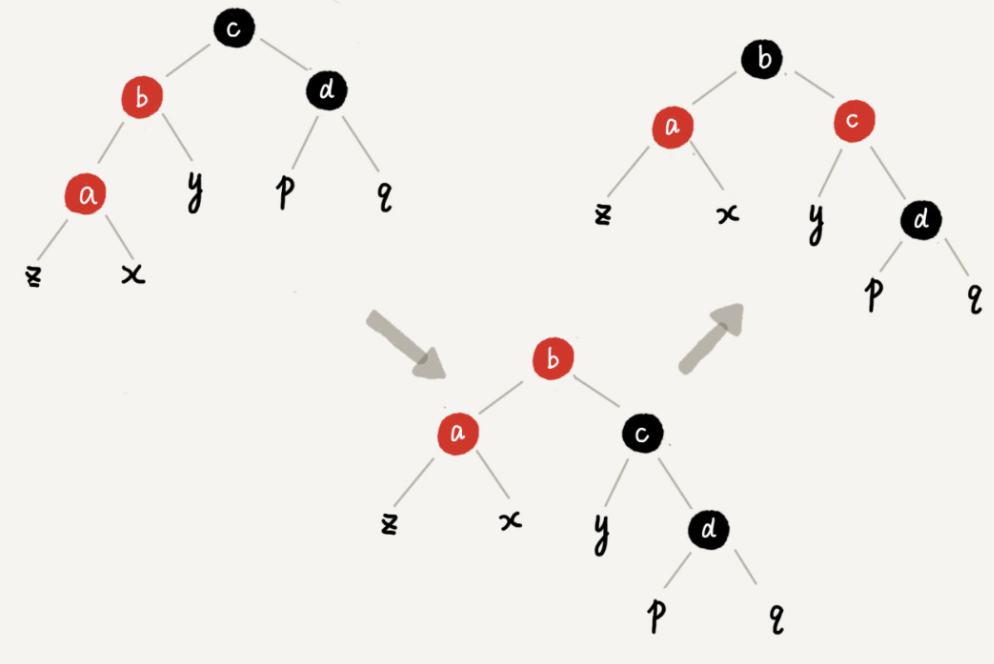
The specific operations are as follows: rotate right around the grandfather node c of the concerned node a; Exchange the colors of parent node b and brother node c of node a, and the adjustment is completed.

The specific codes above are as follows:

   

     

      

     
     

      
    
       /**
      
     

     

      

     
     

      

            * Function Description: insert a node
      
     

     

      

     
     

      

            *
      
     

     

      

     
     

      

            * @author yanfengzhang
      
     

     

      

     
     

      

            * @date 2020-05-27 15:07
      
     

     

      

     
     

      

            */
      
     

     

      

     
     

      
    
       private void insert(RBTreeNode<T> node) {
      
     

     

      

     
     

      
        
       int cmp;
      
     

     

      

     
     

      

               RBTreeNode<T> root = 
       this.rootNode;
      
     

     

      

     
     

      

               RBTreeNode<T> parent = 
       null;
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
        
       /*Under which parent node is the location node added*/
      
     

     

      

     
     

      
        
       while (
       null != root) {
      
     

     

      

     
     

      

                   parent = root;
      
     

     

      

     
     

      

                   cmp = node.key.compareTo(root.key);
      
     

     

      

     
     

      
            
       if (cmp < 
       0) {
      
     

     

      

     
     

      

                       root = root.left;
      
     

     

      

     
     

      

                   } 
       else {
      
     

     

      

     
     

      

                       root = root.right;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

               node.parent = parent;
      
     

     

      

     
     

      
        
       /*It means that there is no node at present, so the newly added node is the root node*/
      
     

     

      

     
     

      
        
       if (
       null == parent) {
      
     

     

      

     
     

      
            
       this.rootNode = node;
      
     

     

      

     
     

      

               } 
       else {
      
     

     

      

     
     

      
            
       //Find the location of the new node under the current parent node
      
     

     

      

     
     

      

                   cmp = node.key.compareTo(parent.key);
      
     

     

      

     
     

      
            
       if (cmp < 
       0) {
      
     

     

      

     
     

      

                       parent.left = node;
      
     

     

      

     
     

      

                   } 
       else {
      
     

     

      

     
     

      

                       parent.right = node;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
        
       /*Set the color of the inserted node to red*/
      
     

     

      

     
     

      

               node.color = COLOR_RED;
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
        
       /*Fixed to red black tree*/
      
     

     

      

     
     

      

               insertFixUp(node);
      
     

     

      

     
     

      

           }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
    
       /**
      
     

     

      

     
     

      

            * Function Description: red black tree insertion correction
      
     

     

      

     
     

      

            *
      
     

     

      

     
     

      

            * @author yanfengzhang
      
     

     

      

     
     

      

            * @date 2020-05-27 15:07
      
     

     

      

     
     

      

            */
      
     

     

      

     
     

      
    
       private void insertFixUp(RBTreeNode<T> node) {
      
     

     

      

     
     

      

               RBTreeNode<T> parent, gparent;
      
     

     

      

     
     

      
        
       /*The parent node of the node exists and is red*/
      
     

     

      

     
     

      
        
       while (((parent = getParent(node)) != 
       null) && isRed(parent)) {
      
     

     

      

     
     

      

                   gparent = getParent(parent);
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
            
       /*What if its grandfather node is empty? What if the parent node is the left child of the grandfather node*/
      
     

     

      

     
     

      
            
       if (parent == gparent.left) {
      
     

     

      

     
     

      

                       RBTreeNode<T> uncle = gparent.right;
      
     

     

      

     
     

      
                
       if ((
       null != uncle) && isRed(uncle)) {
      
     

     

      

     
     

      

                           setColorBlack(uncle);
      
     

     

      

     
     

      

                           setColorBlack(parent);
      
     

     

      

     
     

      

                           setColorRed(gparent);
      
     

     

      

     
     

      

                           node = gparent;
      
     

     

      

     
     

      
                    
       continue;
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
                
       if (parent.right == node) {
      
     

     

      

     
     

      

                           RBTreeNode<T> tmp;
      
     

     

      

     
     

      

                           leftRotate(parent);
      
     

     

      

     
     

      

                           tmp = parent;
      
     

     

      

     
     

      

                           parent = node;
      
     

     

      

     
     

      

                           node = tmp;
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

                       setColorBlack(parent);
      
     

     

      

     
     

      

                       setColorRed(gparent);
      
     

     

      

     
     

      

                       rightRotate(gparent);
      
     

     

      

     
     

      

                   } 
       else {
      
     

     

      

     
     

      

                       RBTreeNode<T> uncle = gparent.left;
      
     

     

      

     
     

      
                
       if ((
       null != uncle) && isRed(uncle)) {
      
     

     

      

     
     

      

                           setColorBlack(uncle);
      
     

     

      

     
     

      

                           setColorBlack(parent);
      
     

     

      

     
     

      

                           setColorRed(gparent);
      
     

     

      

     
     

      

                           node = gparent;
      
     

     

      

     
     

      
                    
       continue;
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
                
       if (parent.left == node) {
      
     

     

      

     
     

      

                           RBTreeNode<T> tmp;
      
     

     

      

     
     

      

                           rightRotate(parent);
      
     

     

      

     
     

      

                           tmp = parent;
      
     

     

      

     
     

      

                           parent = node;
      
     

     

      

     
     

      

                           node = tmp;
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

                       setColorBlack(parent);
      
     

     

      

     
     

      

                       setColorRed(gparent);
      
     

     

      

     
     

      

                       leftRotate(gparent);
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      

               setColorBlack(
       this.rootNode);
      
     

     

      

     
     

      

           }
      
     
   

(3) Balance adjustment for delete operation

The balance adjustment of deletion operation is divided into two steps:

The first step is to make preliminary adjustments for deleting nodes. The preliminary adjustment only ensures that the whole red black tree still meets the requirements of the last definition after a node is deleted, that is, all paths from the node to its leaf nodes contain the same number of black nodes;

The second step is to make secondary adjustment for the concerned node to make it meet the third definition of red black tree, that is, there are no two adjacent red nodes.

1. Preliminary adjustment for deleted nodes

In order to ensure that some nodes in the "black red tree" are defined as "black" or "black", the last node in the "red tree" will only meet the requirements of "black". If a node is marked as "black black", it should be counted as two black nodes when calculating the number of black nodes.

Note: if a node can be either red or black, it is represented by half red and half black in the figure. If a node is "red black" or "black black", a small black dot in the upper left corner is used to represent additional black.

Case 1: if the node to be deleted is a, it has only one child node b

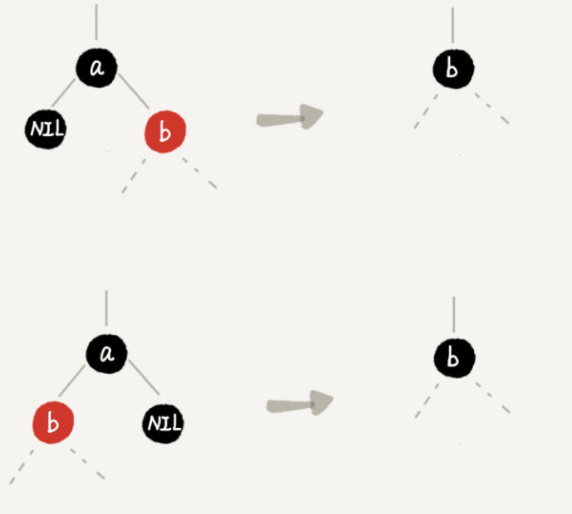
The specific operations are as follows: delete node A and replace node b with node A. This part of the operation is the same as that of ordinary binary search tree; Node a can only be black and node b can only be red. Other situations do not meet the definition of red black tree. In this case, we change node b to black; After adjustment, no secondary adjustment is required.

If a has two non child nodes of c, it is the case that a wants to delete its two child nodes

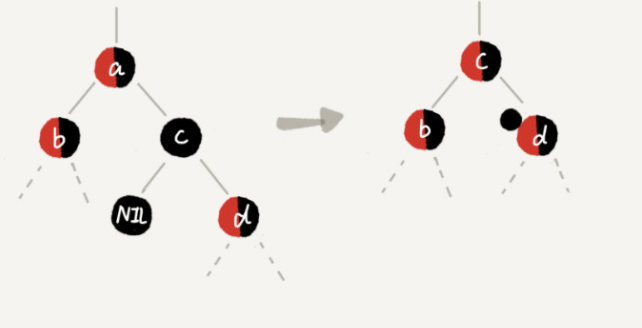
The specific operation is as follows: if the successor node of node a is the right child node c, the right child node c must have no left child tree. We delete node A and replace node c with node a. This part of the operation is no different from the ordinary binary search tree deletion operation; Then set the color of node c to the same color as node a; If node c is black, in order not to violate the last definition of the red black tree, we add a black to the right child node d of node c. at this time, node d becomes "red black" or "black black"; At this time, the concerned node becomes node d, and the second step of adjustment will be done for the concerned node.

Case 3: if node a is to be deleted, it has two non empty child nodes, and the successor node of node a is not a right child node

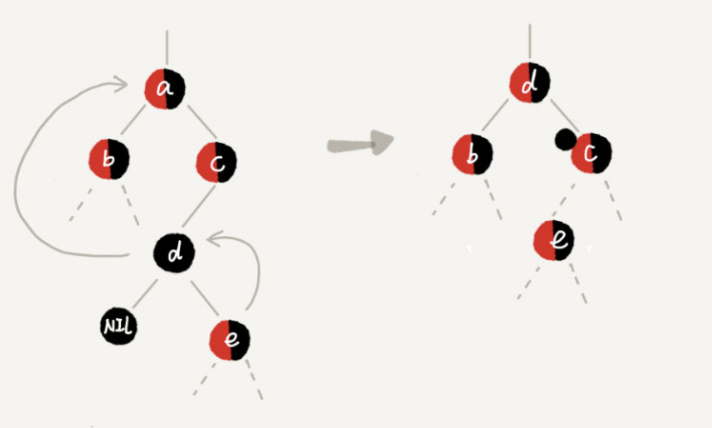
The specific operations are as follows: find the successor node D and delete it. Refer to CASE 1 for the process of deleting the successor node D; Replace node a with subsequent node D; Set the color of node d to the same color as node a; If node D is black, in order not to violate the last definition of the red black tree, we add a black to the right child node c of node D. at this time, node c becomes "red black" or "black black"; At this time, the concerned node becomes node c, and the second step of adjustment will be done for the concerned node.

2. Make secondary adjustment for concerned nodes

After the initial adjustment, the concerned node becomes a "red black" or "black black" node. For this concerned node, the secondary adjustment is carried out in four cases.

Note: the secondary adjustment is to ensure that there are no adjacent red nodes in the red black tree.

Case 1: if the node of interest is a, its brother node c is red

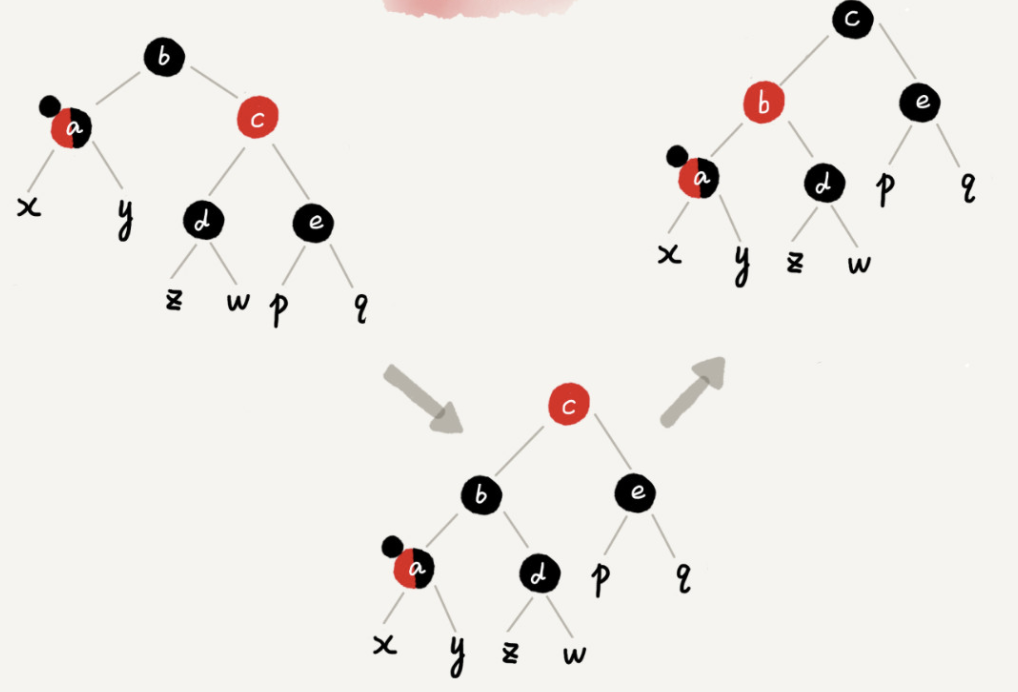
Specific operation: rotate left around the parent node b of the concerned node a; The parent node b and the grandfather node c of the concerned node a exchange colors; The concerned nodes remain unchanged; Continue to select the appropriate rules from the four cases to adjust.

Case 2: if the node of interest is a, its brother node c is black, and the left and right child nodes d and e of node c are black

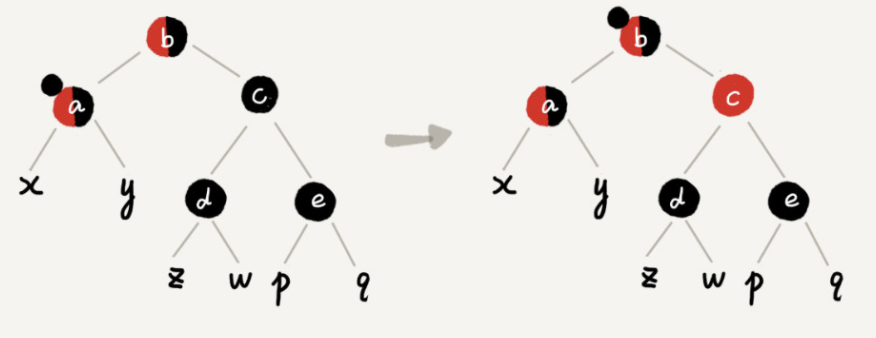
Specific operation: change the color of brother node c of node a to red; Remove a black from the concerned node A. at this time, node a is pure red or black; Add a black to the parent node b of node a, and node b will become "red black" or "black black"; The concerned node changes from a to its parent node b; Continue to select the rules from the four cases to adjust.

Case 3: if the node of interest is a, its brother node c is black, the left child node d of c is red, and the right child node e of c is black

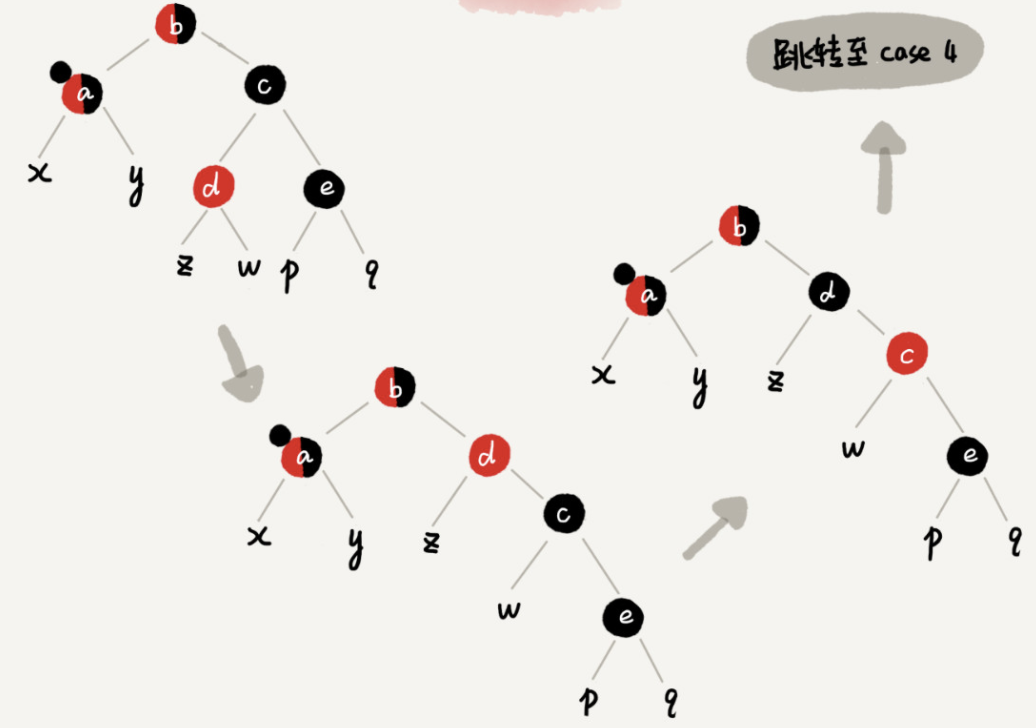
Specific operation: rotate right around the brother node c of the concerned node a; Node c and node d exchange colors; The concerned nodes remain unchanged; Jump to CASE 4 and continue adjustment.

Case 4: if the brother node c of node a is black and the right child node of c is red

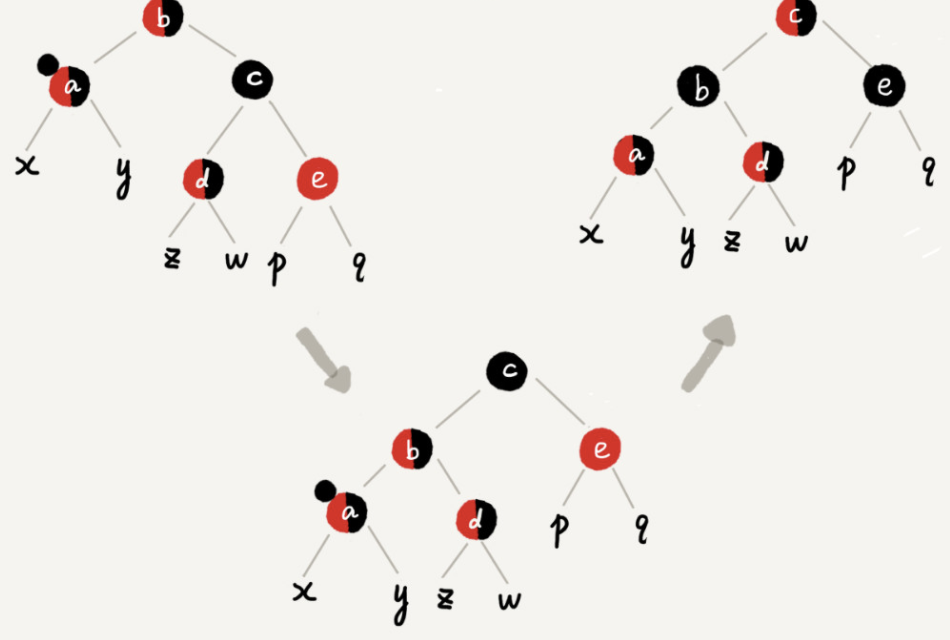
Specific operation: rotate left around the parent node b of the concerned node a; Set the color of the brother node c of the node of interest a to the same color as the parent node b of the node of interest a; Set the color of the parent node a to black; Remove a black from the concerned node a, and node a becomes pure red or black; Set the uncle node e of the concerned node a to black; End of adjustment.

The above specific codes can be seen:

   

     

      

     
     

      
    
       /**
      
     

     

      

     
     

      

            * Function Description: delete node
      
     

     

      

     
     

      

            *
      
     

     

      

     
     

      

            * @author yanfengzhang
      
     

     

      

     
     

      

            * @date 2020-05-27 15:11
      
     

     

      

     
     

      

            */
      
     

     

      

     
     

      
    
       private void remove(RBTreeNode<T> node) {
      
     

     

      

     
     

      

               RBTreeNode<T> child, parent;
      
     

     

      

     
     

      
        
       boolean color;
      
     

     

      

     
     

      
        
       /*The left and right children of the deleted node are not empty*/
      
     

     

      

     
     

      
        
       if ((
       null != node.left) && (
       null != node.right)) {
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
            
       /*Get the successor node of the deleted node*/
      
     

     

      

     
     

      

                   RBTreeNode<T> replace = node;
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

                   replace = replace.right;
      
     

     

      

     
     

      
            
       while (
       null != replace.left) {
      
     

     

      

     
     

      

                       replace = replace.left;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
            
       /*node Node is not a root node*/
      
     

     

      

     
     

      
            
       if (
       null != getParent(node)) {
      
     

     

      

     
     

      
                
       /*node Is the left node*/
      
     

     

      

     
     

      
                
       if (getParent(node).left == node) {
      
     

     

      

     
     

      

                           getParent(node).left = replace;
      
     

     

      

     
     

      

                       } 
       else {
      
     

     

      

     
     

      

                           getParent(node).right = replace;
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      

                   } 
       else {
      
     

     

      

     
     

      
                
       this.rootNode = replace;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

                   child = replace.right;
      
     

     

      

     
     

      

                   parent = getParent(replace);
      
     

     

      

     
     

      

                   color = getColor(replace);
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
            
       if (parent == node) {
      
     

     

      

     
     

      

                       parent = replace;
      
     

     

      

     
     

      

                   } 
       else {
      
     

     

      

     
     

      
                
       if (
       null != child) {
      
     

     

      

     
     

      

                           setParent(child, parent);
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      

                       parent.left = child;
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

                       replace.right = node.right;
      
     

     

      

     
     

      

                       setParent(node.right, replace);
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

                   replace.parent = node.parent;
      
     

     

      

     
     

      

                   replace.color = node.color;
      
     

     

      

     
     

      

                   replace.left = node.left;
      
     

     

      

     
     

      

                   node.left.parent = replace;
      
     

     

      

     
     

      
            
       if (color == COLOR_BLACK) {
      
     

     

      

     
     

      

                       removeFixUp(child, parent);
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

                   node = 
       null;
      
     

     

      

     
     

      
            
       return;
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
        
       if (
       null != node.left) {
      
     

     

      

     
     

      

                   child = node.left;
      
     

     

      

     
     

      

               } 
       else {
      
     

     

      

     
     

      

                   child = node.right;
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

               parent = node.parent;
      
     

     

      

     
     

      

               color = node.color;
      
     

     

      

     
     

      
        
       if (
       null != child) {
      
     

     

      

     
     

      

                   child.parent = parent;
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
        
       if (
       null != parent) {
      
     

     

      

     
     

      
            
       if (parent.left == node) {
      
     

     

      

     
     

      

                       parent.left = child;
      
     

     

      

     
     

      

                   } 
       else {
      
     

     

      

     
     

      

                       parent.right = child;
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      

               } 
       else {
      
     

     

      

     
     

      
            
       this.rootNode = child;
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
        
       if (color == COLOR_BLACK) {
      
     

     

      

     
     

      

                   removeFixUp(child, parent);
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      

               node = 
       null;
      
     

     

      

     
     

      

           }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
    
       /**
      
     

     

      

     
     

      

            * Function Description: delete repair
      
     

     

      

     
     

      

            *
      
     

     

      

     
     

      

            * @author yanfengzhang
      
     

     

      

     
     

      

            * @date 2020-05-27 15:11
      
     

     

      

     
     

      

            */
      
     

     

      

     
     

      
    
       private void removeFixUp(RBTreeNode<T> node, RBTreeNode<T> parent) {
      
     

     

      

     
     

      

               RBTreeNode<T> other;
      
     

     

      

     
     

      
        
       /*node It is not empty and black, and it is not the root node*/
      
     

     

      

     
     

      
        
       while ((
       null == node || isBlack(node)) && (node != 
       this.rootNode)) {
      
     

     

      

     
     

      
            
       /*node Is the left child of the parent node*/
      
     

     

      

     
     

      
            
       if (node == parent.left) {
      
     

     

      

     
     

      
                
       /*Get its right child*/
      
     

     

      

     
     

      

                       other = parent.right;
      
     

     

      

     
     

      
                
       /*node The sibling node of the node is red*/
      
     

     

      

     
     

      
                
       if (isRed(other)) {
      
     

     

      

     
     

      

                           setColorBlack(other);
      
     

     

      

     
     

      

                           setColorRed(parent);
      
     

     

      

     
     

      

                           leftRotate(parent);
      
     

     

      

     
     

      

                           other = parent.right;
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
                
       /*node The sibling node of the node is black, and the two child nodes of the sibling node are also black*/
      
     

     

      

     
     

      
                
       if ((other.left == 
       null || isBlack(other.left)) &&
      
     

     

      

     
     

      

                               (other.right == 
       null || isBlack(other.right))) {
      
     

     

      

     
     

      

                           setColorRed(other);
      
     

     

      

     
     

      

                           node = parent;
      
     

     

      

     
     

      

                           parent = getParent(node);
      
     

     

      

     
     

      

                       } 
       else {
      
     

     

      

     
     

      
                    
       /*node The sibling node of the node is black, and the right child of the sibling node is red*/
      
     

     

      

     
     

      
                    
       if (
       null == other.right || isBlack(other.right)) {
      
     

     

      

     
     

      

                               setColorBlack(other.left);
      
     

     

      

     
     

      

                               setColorRed(other);
      
     

     

      

     
     

      

                               rightRotate(other);
      
     

     

      

     
     

      

                               other = parent.right;
      
     

     

      

     
     

      

                           }
      
     

     

      

     
     

      
                    
       /*node The sibling node of the node is black, and the right child of the sibling node is red, and the left child is any color*/
      
     

     

      

     
     

      

                           setColor(other, getColor(parent));
      
     

     

      

     
     

      

                           setColorBlack(parent);
      
     

     

      

     
     

      

                           setColorBlack(other.right);
      
     

     

      

     
     

      

                           leftRotate(parent);
      
     

     

      

     
     

      

                           node = 
       this.rootNode;
      
     

     

      

     
     

      
                    
       break;
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      

                   } 
       else {
      
     

     

      

     
     

      

                       other = parent.left;
      
     

     

      

     
     

      
                
       if (isRed(other)) {
      
     

     

      

     
     

      

                           setColorBlack(other);
      
     

     

      

     
     

      

                           setColorRed(parent);
      
     

     

      

     
     

      

                           rightRotate(parent);
      
     

     

      

     
     

      

                           other = parent.left;
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
                
       if ((
       null == other.left || isBlack(other.left)) &&
      
     

     

      

     
     

      

                               (
       null == other.right || isBlack(other.right))) {
      
     

     

      

     
     

      

                           setColorRed(other);
      
     

     

      

     
     

      

                           node = parent;
      
     

     

      

     
     

      

                           parent = getParent(node);
      
     

     

      

     
     

      

                       } 
       else {
      
     

     

      

     
     

      
                    
       if (
       null == other.left || isBlack(other.left)) {
      
     

     

      

     
     

      

                               setColorBlack(other.right);
      
     

     

      

     
     

      

                               setColorRed(other);
      
     

     

      

     
     

      

                               leftRotate(other);
      
     

     

      

     
     

      

                               other = parent.left;
      
     

     

      

     
     

      

                           }
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

                           setColor(other, getColor(parent));
      
     

     

      

     
     

      

                           setColorBlack(parent);
      
     

     

      

     
     

      

                           setColorBlack(other.left);
      
     

     

      

     
     

      

                           rightRotate(parent);
      
     

     

      

     
     

      

                           node = 
       this.rootNode;
      
     

     

      

     
     

      
                    
       break;
      
     

     

      

     
     

      

                       }
      
     

     

      

     
     

      

                   }
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      
        
       if (node != 
       null) {
      
     

     

      

     
     

      

                   setColorBlack(node);
      
     

     

      

     
     

      

               }
      
     

     

      

     
     

      

           }
      
     
   

References and links:

1.https://tech.meituan.com/2016/12/02/redblack-tree.html

2. The beauty of data structure and algorithm, Wang Zheng (former Google Engineer), geek time, 2019

3.https://blog.csdn.net/tanrui519521/article/details/80980135

4.https://blog.csdn.net/jjc120074203/article/details/78780221

5.https://blog.csdn.net/aa1215018028/article/details/92660140