catalogue
A - furnace stone of Xiaosha
Original title link: https://ac.nowcoder.com/acm/contest/23477/A
Problem solving ideas: mathematical problems, conclusion problems. First of all, a very important point is that if the use of attack card is a fixed value, our attack range is any damage value in an interval. Set the attack card to be used a times and the reply card to be used b times (one of the implied conditions is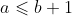 
), then the minimum damage is to use up the attack cards of a time on the basis of using the recovery card, and finally use up all the recovery cards. The damage caused is
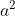； The maximum damage is to use up all the recovery cards of times b before using the attack card. The damage caused is
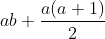. For different intervals with different numbers of attack cards, you can calculate under what conditions they can be merged, that is, make the right end point of the previous interval greater than or equal to the left end point of the current interval minus one, that is
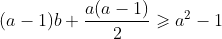, will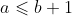Substitute in, you can solve it
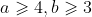When the interval can be merged, only special judgment is required
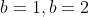When b = 1, the intervals are [1, 2], [4, 5]; When b = 2, the intervals are [1, 3], [4, 7], [9, 12], respectively. It can be found that only when b = 1 and x = 3 ， and b = 2 and x = 8 cannot be merged. In other cases, you can kill as long as X is less than or equal to the maximum damage, otherwise you can't kill.
AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
ll n, m, k;
cin >> n >> m >> k;
ll a = min(n, m + 1);
ll ans = a * m + a * (a + 1) / 2;
while(k--){
ll x;
cin >> x;
if(m == 1 && x == 3 || m == 2 && x == 8){
cout << "NO" << endl;
continue;
}
if(x <= ans) cout << "YES" << endl;
else cout << "NO" << endl;
}
return 0;
}B - little sand's magic
Original title link: https://ac.nowcoder.com/acm/contest/23477/B
Problem solving idea: give priority to the channels related to cities that need to rise more to form a pole Dalian sub graph (multiple pole Dalian sub graphs will be formed), so that each pole Dalian sub graph only needs to operate the times of the maximum rise height to complete the height that needs to rise, and the remaining cities can operate separately due to insufficient operands. During the specific operation, you can first accumulate the height that each city needs to rise, and record and sort the minimum height that two cities with channels need to rise. Operation 1 is carried out through the search and merging of the joint query set. When merging, subtract the minimum rising height of the two cities from the previously accumulated number (because only the number of times of operating the maximum rising height is required in a polar Dalian Tong subgraph).
AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 500005, M = 5000005;
int f[M]; // f[i] indicates the ancestor of node i (f[i] = i indicates that I is an isolated node)
ll h[N]; // h[i] indicates the height that the ith city needs to rise
struct node{
int x, y;
int height;
bool operator < (const node &u) const{
return height > u.height;
}
}e[M];
int find(int x){
if(f[x] != x) f[x] = find(f[x]);
return f[x];
}
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, m;
cin >> n >> m;
ll ans = 0;
for(int i = 1; i <= n; i++){
cin >> h[i];
ans += h[i];
f[i] = i;
}
for(int i = 1; i <= m; i++){
cin >> e[i].x >> e[i].y;
e[i].height = min(h[e[i].x], h[e[i].y]);
}
sort(e + 1, e + m + 1);
int x = min(5 * n, m);
for(int i = 1; i <= m; i++){
if(x == 0) break;
int a = find(e[i].x), b = find(e[i].y);
if(a != b){
ans -= e[i].height;
f[a] = b;
x--;
}
}
cout << ans << endl;
return 0;
}C-xiaosha's kill
Original title link: https://ac.nowcoder.com/acm/contest/23477/C
Problem solving ideas: check in the problem. Judge whether your physical strength is enough to kill the ball when you encounter 1. If not, choose not to kill and recover your physical strength; Recover your strength when you encounter 0.
AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
ll x, a, b;
cin >> x >> a >> b;
string s;
cin >> s;
int len = s.size();
int cnt = 0;
for(int i = 0; i < len; i++){
if(s[i] == '1' && x >= a){
x -= a;
cnt++;
}
else x += b;
}
cout << cnt << endl;
return 0;
}D-coloring of small sand
Original title link: https://ac.nowcoder.com/acm/contest/23477/D
Problem solving idea: large simulation construction problem. Construct according to the values of N% 3 when they are 0, 1 and 2 respectively (there are many construction methods, one of which is used in the following code). Note that the meaning of the question cannot be satisfied when n% 3 = 0. In addition, it is also necessary to judge the situation when n == 1.
AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 1005;
int n, idx;
int a[N][N];
void draw1(int x, int y){ // 1 1
for(int i = x; i <= n; i += 3){ // 1 2
for(int j = y; j <= n; j += 2){ // 2 2
a[i][j] = a[i][j + 1] = a[i + 1][j] = ++idx;
a[i + 1][j + 1] = a[i + 2][j] = a[i + 2][j + 1] = ++idx;
}
}
}
// 1
void draw2(int x){ // 1 1 2
for(int i = x; i <= n; i++){ // 2 2
if(i & 1) a[i - 1][1] = a[i][1] = a[i][2] = ++idx;
else a[i - 1][3] = a[i][2] = a[i][3] = ++idx;
}
}
void draw3(int x, int y){ // 1 1 2
for(int j = y; j <= n; j += 3){ // 1 2 2
a[x][j] = a[x][j + 1] = a[x + 1][j] = ++idx;
a[x][j + 2] = a[x + 1][j + 2] = a[x + 1][j + 1] = ++idx;
}
}
void pf(){
cout << "YES" << endl;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
cout << a[i][j] << ' ';
}
cout << endl;
}
}
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n;
if(n % 3 == 0) cout << "NO" << endl;
else if(n == 1) cout << "YES" << endl << 0 << endl;
else if(n % 3 == 1){
idx = 5;
a[1][1] = a[1][2] = a[2][1] = 1;
a[4][3] = a[4][4] = a[3][4] = 2;
a[3][1] = a[3][2] = a[4][2] = 3;
a[2][2] = a[2][3] = a[3][3] = 4;
a[1][3] = a[1][4] = a[2][4] = 5;
draw3(1, 5);
draw3(3, 5);
if(n & 1) draw2(5), draw1(5, 4);
else draw1(5, 1);
pf();
}
else if(n % 3 == 2){
a[1][1] = a[1][2] = a[2][2] = ++idx;
draw3(1, 3);
if(n & 1) draw2(3), draw1(3, 4);
else draw1(3, 1);
pf();
}
return 0;
}E-xiaosha's long road
Original title link: https://ac.nowcoder.com/acm/contest/23477/E
Solution idea: In conclusion, the minimum value is to construct a directed graph as acyclic as possible, so that it can experience each point at most once, and the path length is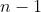
； The maximum value is to delete the shortest number of edges in the complete graph to construct an Euler trace (Euler path), that is, as long as only two node degrees are controlled to be odd and the degrees of other nodes are even, for the complete graph with odd nodes, the degrees of each edge are even, so the maximum value is the number of edges of the complete graph
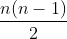； For a complete graph with even nodes, the degree of each edge is odd and must be deleted in order to control it into Euler trace
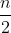One more step can be taken after the edge becomes an Euler trace, so the maximum value is
.
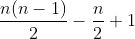AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
ll n;
cin >> n;
cout << n - 1 << ' ';
if(n & 1) cout << n * (n - 1) / 2 << endl;
else cout << n * (n - 1) / 2 - n / 2 + 1 << endl;
return 0;
}F-calculation of small sand
Original title link: https://ac.nowcoder.com/acm/contest/23477/F
Solution idea: because the multiplication sign has high priority, each plus sign can be used as a separator to separate into several intervals. The value of each interval is preprocessed separately, and then the value of the corresponding interval is modified in each query, and the formula result output is calculated. (due to the large value, the module needs to be taken, the division needs to be multiplied by its inverse element, and the module needs to be added for subtraction)
AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f;
const int mod = 1000000007;
const int N = 1000005;
char s[N];
ll a[N], pa[N], b[N];
ll qmi(ll a, ll b){
ll res = 1;
a %= mod;
while(b){
if(b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
ll inv(ll x){
return qmi(x, mod - 2) % mod;
}
int main(){
int n, q;
cin >> n >> q;
cin >> s + 1;
s[n] = '+';
for(int i = 1; i <= n; i++) cin >> a[i];
ll pos = 0, now = 1;
memset(pa, -1, sizeof pa);
for(int i = 1; i <= n; i++){
now = now * a[i] % mod;
if(s[i] == '+'){
pa[i] = pos;
b[pos++] = now;
now = 1;
}
else pa[i] = pos;
}
ll x, y, ans = 0;
for(int i = 0; i < pos; i++) ans = (ans + b[i]) % mod;
while(q--){
cin >> x >> y;
int pos = pa[x];
ll tmp = b[pos] * y % mod * inv(a[x]) % mod;
if(tmp >= b[pos]) ans = (ans + (tmp - b[pos] + mod) % mod) % mod;
else ans = (ans - (b[pos] - tmp + mod) % mod + mod) % mod;
a[x] = y;
b[pos] = tmp;
cout << ans << endl;
}
return 0;
}G-xiaosha's body method
Original title link: https://ac.nowcoder.com/acm/contest/23477/G
Solution idea: LCA algorithm, tree difference idea. Store the tree with adjacency table (bidirectional), and store the prefix sum of each node from top to bottom and from bottom to top through dfs (set from bottom to top)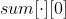
Storage, from top to bottom
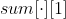Storage). Then the total physical consumption is the consumption of jumping from the ground to the starting point u, plus the consumption of u from the bottom to the minimum common ancestor node of u and v, plus the consumption of u from the minimum common ancestor node of u and v to node v, that is
.
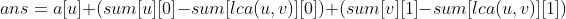AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 1000005, M = 2000005;
int a[N], h[N], e[M], ne[M], idx;
int fa[N][20], deep[N]; // fa[i][j] represents the 2nd ^ J ancestor of node I
ll sum[N][2]; // sum[i][0] refers to the prefix and sum of node i jumping (from bottom to top) to the ancestor node
// sum[i][1] represents the prefix and sum of the parent node of node i jumping (from top to bottom) to node I
void add(int a, int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u, int f){
fa[u][0] = f;
deep[u] = deep[f] + 1;
sum[u][0] = sum[f][0] + max(0, a[f] - a[u]);
sum[u][1] = sum[f][1] + max(0, a[u] - a[f]);
for(int i = 1; i < 20; i++){
fa[u][i] = fa[fa[u][i - 1]][i - 1];
}
for(int i = h[u]; i != -1; i = ne[i]){
int v = e[i];
if(v != f) dfs(v, u);
}
}
int lca(int x, int y){
if(deep[x] < deep[y]) swap(x, y);
for(int i = 19; i >= 0; i--){
if(deep[fa[x][i]] >= deep[y]){
x = fa[x][i];
}
}
if(x == y) return y;
for(int i = 19; i >= 0; i--){
if(fa[x][i] != fa[y][i]){
x = fa[x][i];
y = fa[y][i];
}
}
return fa[x][0];
}
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, m;
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i < n; i++){
int x, y;
cin >> x >> y;
add(x, y);
add(y, x);
}
dfs(1, 0);
while(m--){
int u, v;
cin >> u >> v;
cout << a[u] + sum[u][0] + sum[v][1] - sum[lca(u, v)][0] - sum[lca(u, v)][1] << endl;
}
return 0;
}H-number of small sand
Original title link: https://ac.nowcoder.com/acm/contest/23477/H
Problem solving idea: according to binary splitting, the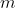
Split into 0 or 1 for each bit
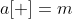And
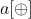Maximum, it is necessary to ensure that each number can only have one 1 in the same binary bit, that is, guarantee
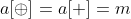. Then, since each bit does not interfere with each other, the possible situation is
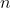Under binary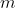Yes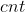
1, then the total number of schemes is
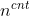Species.
AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1000000007;
ll quick_pow(ll a, ll b){
ll res = 1;
a %= mod;
while(b){
if(b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
ll n, m;
cin >> n >> m;
ll cnt = 0;
while(m){
if(m & 1) cnt++;
m >>= 1;
}
cout << quick_pow(n, cnt) << endl;
return 0;
}I-structure of Xiaosha
Original title link: https://ac.nowcoder.com/acm/contest/23477/I
Problem solving ideas: simulation problems with more details. Since the first 25 characters are individually symmetrical, only one is used when using two identical characters, and the last 10 characters are matched symmetrically. Two are used when using a pair of characters. Also noteThe writing method of odd and even numbers is different, and pay attention to the special judgment of conditions when they are not tenable.
AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
string s = "\"!'*+-.08:=^_WTYUIOAHXVM|", l = "<\\[{(", r = ">/]})", ans;
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, m;
cin >> n >> m;
if(n == m && n == 1) cout << s[24];
for(int i = 0; i < 5; m -= 2, i++){
if(m <= 2 && (n & 1 || m <= 1)) break;
ans = l[i] + ans + r[i];
}
for(int i = 0; i < 24; m--, i++){
if(m <= 1) break;
ans = s[i] + ans + s[i];
}
if(ans.size() >= n || m > 1) cout << -1;
else{
while(ans.size() + 2 <= n)
if(m == 1) ans = s[24] + ans + s[24];
else ans = l[0] + ans + r[0];
if(n & 1){
for(int i = 0; i < n - 1; i++){
if(i == n / 2) cout << s[24];
cout << ans[i];
}
}
else cout << ans;
}
return 0;
}J-Dota of Xiaosha
Original title link: https://ac.nowcoder.com/acm/contest/23477/J
Problem solving idea: for different skills, the three magic balls needed to cast are different and can be stored in a list. The two operations that need to be carried out are release skill (interval query) and modification method (fixed-point modification), and the amount of data is not small, which can be realized by maintaining DDP through line segment tree. Since the casting skill is only related to the attribute of the magic ball and has nothing to do with the order, the three magic balls of each skill can be arranged in up to 6 ways. You can use next_permutation(). Pre process the relationship between each skill before operation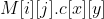
(indicates the relationship between the x-th arrangement of skill i and the y-th arrangement of skill j). For the meaning of values 0, 1, 2 and 3, refer to the following code.
AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 100005;
int a[N];
int skill[10][3] = { // 1 for fireball, 2 for thunder ball and 3 for ice hockey
{1, 1, 1}, {1, 1, 2}, {1, 1, 3},
{3, 3, 3}, {3, 3, 1}, {3, 3, 2},
{2, 2, 2}, {2, 2, 1}, {2, 2, 3}, {1, 2, 3}
};
struct Matrix{ // matrix
int c[6][6];
Matrix(){
for(int i = 0; i < 6; i++)
for(int j = 0; j < 6; j++)
c[i][j] = ((i == j) ? 0 : INF);
}
}M[10][10];
Matrix operator * (Matrix A, Matrix B){ // Matrix multiplication overload
Matrix C;
for(int i = 0; i < 6; i++){
for(int j = 0; j < 6; j++){
C.c[i][j] = INF;
for(int k = 0; k < 6; k++){
C.c[i][j] = min(C.c[i][j], A.c[i][k] + B.c[k][j]);
}
}
}
return C;
}
struct sgt_tree{ // Segment tree node
int lchild, rchild;
Matrix v;
}sgt[4 * N];
int root, topt;
void sgt_build(int &now, int l, int r){ // Segment tree establishment
if(!now) now = ++topt;
if(l == r){
sgt[now].v = M[a[l]][a[l + 1]];
return;
}
int mid = l + r >> 1;
sgt_build(sgt[now].lchild, l, mid);
sgt_build(sgt[now].rchild, mid + 1, r);
sgt[now].v = sgt[sgt[now].lchild].v * sgt[sgt[now].rchild].v;
}
void sgt_modify(int &now, int l, int r, int k){ // Segment tree modification
if(!now) now = ++topt;
int mid = l + r >> 1;
if(l == r){
sgt[now].v = M[a[l]][a[l + 1]];
return;
}
if(k <= mid) sgt_modify(sgt[now].lchild, l, mid, k);
else sgt_modify(sgt[now].rchild, mid + 1, r, k);
sgt[now].v = sgt[sgt[now].lchild].v * sgt[sgt[now].rchild].v;
}
Matrix res;
void sgt_query(int &now, int l, int r, int x, int y){ // Segment tree query
if(!now) now = ++topt;
int mid = l + r >> 1;
if(l >= x && r <= y){
res = res * sgt[now].v;
return;
}
if(x <= mid) sgt_query(sgt[now].lchild, l, mid, x, y);
if(y > mid) sgt_query(sgt[now].rchild, mid + 1, r, x, y);
}
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> a[i];
a[i]--;
}
// Preprocessing the relationship between different skills
int s1[3], s2[3];
for(int i = 0; i < 10; i++){
for(int j = 0; j < 10; j++){
for(int k = 0; k < 3; k++){
s1[k] = skill[i][k];
s2[k] = skill[j][k];
}
for(int x = 0; x < 6; x++){
for(int y = 0; y < 6; y++){
if(s1[0] == s2[0] && s1[1] == s2[1] && s1[2] == s2[2]) M[i][j].c[x][y] = 0;
else if(s1[1] == s2[0] && s1[2] == s2[1]) M[i][j].c[x][y] = 1;
else if(s1[2] == s2[0]) M[i][j].c[x][y] = 2;
else M[i][j].c[x][y] = 3;
next_permutation(s2, s2 + 3);
}
next_permutation(s1, s1 + 3);
}
}
}
sgt_build(root, 1, n - 1);
int op, l, r;
while(m--){
cin >> op >> l >> r;
if(op == 1){
if(l == r){
cout << 3 << endl;
continue;
}
Matrix zero;
res = zero; // Initialize res matrix
sgt_query(root, 1, n - 1, l, r - 1);
int ans = INF;
for(int i = 0; i < 6; i++){
for(int j = 0; j < 6; j++){
ans = min(ans, res.c[i][j]);
}
}
cout << ans + 3 << endl;
}
if(op == 2){
a[l] = r - 1;
if(l != 1) sgt_modify(root, 1, n - 1, l - 1);
if(l != n) sgt_modify(root, 1, n - 1, l);
}
}
return 0;
}K-little sand's pace
Original title link: https://ac.nowcoder.com/acm/contest/23477/K
Solution idea: check in the question. Each step will make that point and 5 point pass through once (both past and back). Note that when 5 appears, there is no need to move.
AC Code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <cctype>
#include <utility>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
int cnt[10];
int main(){
//freopen("input.txt", "r", stdin);
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
string s;
cin >> s;
int n = s.size();
for(int i = 0; i < n; i++){
if(s[i] != '5'){
cnt[s[i] - '0']++;
cnt[5]++;
}
}
for(int i = 1; i < 9; i++)
cout << cnt[i] << ' ';
cout << cnt[9] << endl;
return 0;
}50. remake of M-xiaosha
Link to the original title of ordinary version: https://ac.nowcoder.com/acm/contest/23477/L
Link to the original title of racing Edition: https://ac.nowcoder.com/acm/contest/23477/M
Problem solving idea: tree array maintains dynamic prefix and. First sort according to the air transportation value, then traverse the air transportation, and find the current point and the front of the current point each time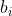 
The interval sum of bits, and the value is added to the tree array of the current bit subscript for update. Finally, query n, and the query result is the required number of schemes.
AC Code:
#include<bits/stdc++.h>
namespace GenHelper
{
int z1,z2,z3,z4,z5,u,res;
int get()
{
z5=((z1<<6)^z1)>>13;
z1=((int)(z1&4294967)<<18)^z5;
z5=((z2<<2)^z2)>>27;
z2=((z2&4294968)<<2)^z5;
z5=((z3<<13)^z3)>>21;
z3=((z3&4294967)<<7)^z5;
z5=((z4<<3)^z4)>>12;
z4=((z4&4294967)<<13)^z5;
return (z1^z2^z3^z4);
}
int read(int m) {
u=get();
u>>=1;
if(m==0)res=u;
else res=(u/2345+1000054321)%m;
return res;
}
void srand(int x)
{
z1=x;
z2=(~x)^(0x23333333);
z3=x^(0x12345798);
z4=(~x)+51;
u = 0;
}
}
using namespace GenHelper;
using namespace std;
typedef long long ll;
const int N=2e6+7,mod=1e9+7;
int a[N],b[N];
ll tree[N];
struct node{
int id, x;
bool operator < (const node &u) const{
return x == u.x ? id < u.id : x < u.x;
}
}s[N];
inline int lowbit(int x){
return x & -x;
}
void add(int x, ll c){
while(x < N){
tree[x] = (tree[x] + c) % mod;
x += lowbit(x);
}
}
ll ask(ll x){
ll res = 0;
while(x){
res = (res + tree[x]) % mod;
x -= lowbit(x);
}
return res;
}
int main(){
int n,seed;
scanf("%d %d",&n,&seed);
srand(seed);
for(int i=1;i<=n;i++){
a[i]=read(0),b[i]=read(i);
s[i].id = i, s[i].x = a[i];
}
sort(s + 1, s + n + 1);
for(int i = 1; i <= n; i++){
int id = s[i].id;
ll x = (ask(id - 1) - ask(id - b[id] - 1) + 1 + mod) % mod;
add(id, x);
}
printf("%lld\n", ask(n));
return 0;
}