🔒 Quick navigation and articles related to this article 🔒
| Basic use of set and map | Click through to the article |
|---|---|
| Red black tree | Click through to the article |
Red black tree code
We want to encapsulate the red black tree of KV model and simulate the implementation of set and map. The code used is as follows
#include<iostream>
using namespace std;
enum Color
{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;//Left child of node
RBTreeNode<K, V>* _right;//Right child of node
RBTreeNode<K, V>* _parent;//Parents of nodes
pair<K, V>_kv;
Color _color;//The color of the node
RBTreeNode(const pair<K,V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_color(RED)
{}
};
template<class K, class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public:
RBTree()
:_root(nullptr)
{}
pair<Node*, bool> insert(const pair<K, V>& kv)
{
//1. The tree is empty
if (_root == nullptr)
{
_root = new Node(kv);
_root->_color = BLACK;//The root node is black
return make_pair(_root, true);
}
//Tree is not empty
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//The key of the new node is larger than the current node and goes to the right
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
//The new node key is smaller than the current node to the left
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(cur, false);
}
}
cur = new Node(kv);
Node* newnode = cur;
newnode->_color = RED;
if (parent->_kv.first < kv.first)
{
parent->_right = newnode;
newnode->_parent = parent;
}
else
{
parent->_left = newnode;
newnode->_parent = parent;
}
//Start adjusting color
//The father exists and is red
while (parent && parent->_color == RED)
{
Node* grandParent = parent->_parent;
//parent is grandParent's left child
if (grandParent->_left == parent)
{
Node* uncle = grandParent->_right;
//Uncle exists and is red. Both father and uncle are black
//The ancestor is set to red. If not, the black node of each path will change
if (uncle && uncle->_color == RED)
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandParent->_color = RED;
//Continue to increase
cur = grandParent;
parent = cur->_parent;
}
else//Uncle does not exist or uncle exists and is black
{
if (parent->_left == cur)
{ //Right single rotation
RotateR(grandParent);
parent->_color = BLACK;
grandParent->_color = RED;
}
else //parent->_right == cur
{
RotateL(parent);
RotateR(grandParent);
grandParent->_color = RED;
cur->_color = BLACK;
}
break;
}
}
else //parent is grandParent's left child
{
Node* uncle = grandParent->_left;
if (uncle && uncle->_color == RED)
{
uncle->_color = BLACK;
parent->_color = BLACK;
grandParent->_color = RED;
cur = grandParent;
parent = cur->_parent;
}
else
{
if (parent->_right == cur)
{
RotateL(grandParent);
parent->_color = BLACK;
grandParent->_color = RED;
}
else
{
RotateR(parent);
RotateL(grandParent);
cur->_color = BLACK;
grandParent->_color = RED;
}
break;
}
}
}
_root->_color = BLACK;
return make_pair(newnode, true);
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* parentParent = parent->_parent;
//Rotate first
parent->_right = subRL;
subR->_left = parent;
parent->_parent = subR;
//Changing father node
if (subRL)
subRL->_parent = parent;
if (_root == parent)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
//After the subR is rotated, there may be two cases of left and right subtrees
if (parentParent->_left == parent)
parentParent->_left = subR;
else
parentParent->_right = subR;
subR->_parent = parentParent;
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* parentParent = parent->_parent;//Record the parent node of the parent
//subLR as parent - >_ left
parent->_left = subLR;
subL->_right = parent;
//Update the parent s of the two nodes at the same time
//Note that the subLR may also be an empty node
if (subLR)
subLR->_parent = parent;
parent->_parent = subL;
//The parent may be a separate tree or a subtree, depending on the situation
if (_root == parent)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
//It is also possible that the parent is a subtree or a left subtree
if (parentParent->_left == parent)
parentParent->_left = subL;
else
//It may also be a right subtree
parentParent->_right = subL;
//Adjust the parent node of subL
subL->_parent = parentParent;
}
}
void Destory(Node* root)
{
if (root == nullptr)
{
return;
}
Destory(root->_left);
Destory(root->_right);
delete root;
}
~RBTree()
{
Destory(_root);
_root = nullptr;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first > key)
{
cur = cur->_left;
}
else if (cur->_kv.first < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return nullptr;
}
private:
Node* _root;
};
Template parameters of red black tree
Through the use of set and map, we know that set is K model and map is KV model. How can we use a red black tree to realize set and map?
set container. The template parameters passed into the underlying red black tree are Key and Key:
template<class K>
class set
{
public:
//...
private:
RBTree<K, K> _t;
};
The map container passes in Key and Key value pairs:
template<class K, class V>
class set
{
public:
//...
private:
RBTree<K, pair<K,V> _t;
};
Therefore, the original template parameter of our red black tree is changed from V to T.
template<class K, class T>
class RBTree
{}
Can the red black tree not use the first template parameter? The answer is No.
There is no problem with the set container. Its two parameters are keys. However, map is OK. The find and erase interfaces of map only provide keys. There is a problem without the first template parameter.
Data storage of red black tree nodes
We can first look at how the source code is implemented:
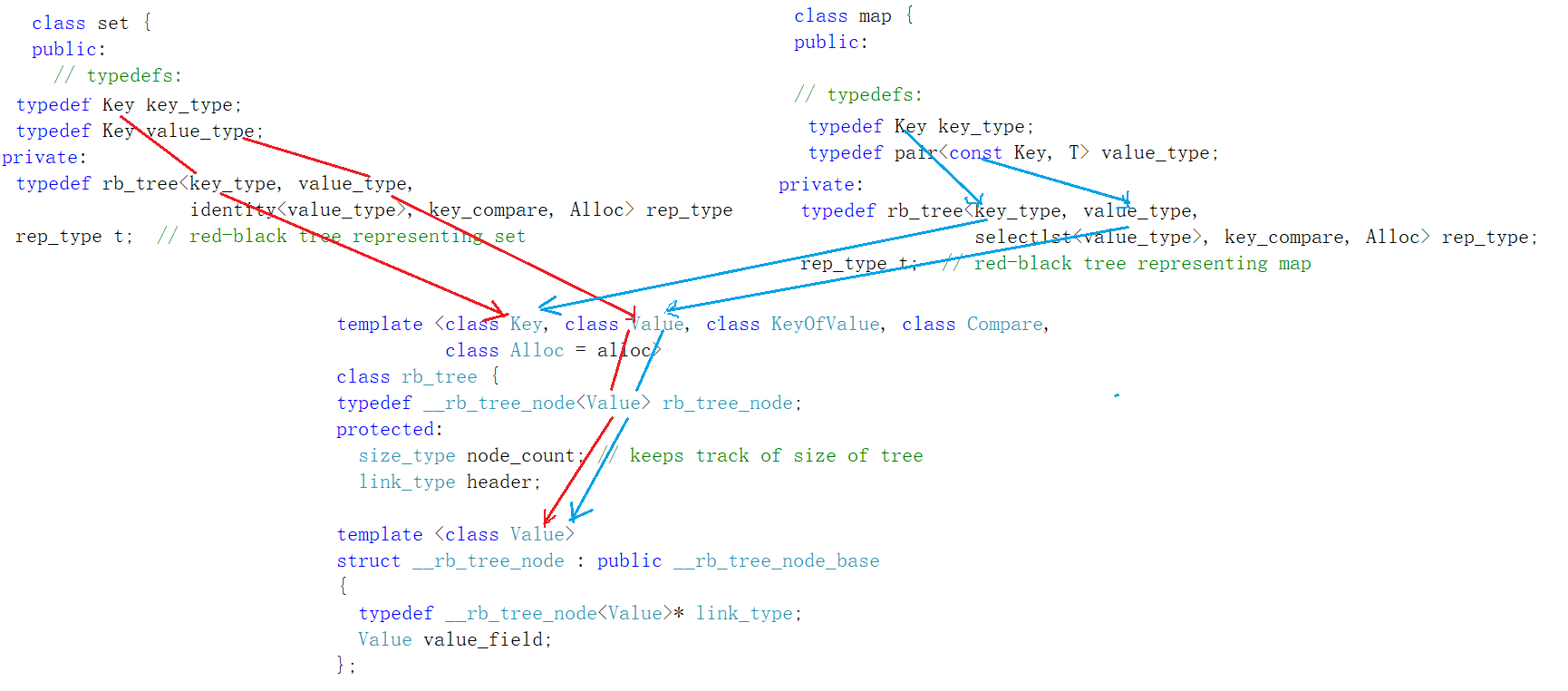
We can see that the Value is stored in the node in the source code. The Key of set is passed to Key and value_type, and the Key and pair < > of map are passed to value_type. If the Value is the Key, then the Key is stored in the node, and if the Value is the pair, then the pair is stored in the node.
Then we can use T to realize it ourselves.
Updated code:
enum Color
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;//Left child of node
RBTreeNode<T>* _right;//Right child of node
RBTreeNode<T>* _parent;//Parents of nodes
T _data;//Stored data
Color _color;//The color of the node
RBTreeNode(const T& x)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_data(x)
,_color(RED)
{}
};
In this way, it doesn't matter whether you are K or KV. I am what you are.
Increase of affine function
There are still problems to be solved. T in red and black trees may be K or pair < >. How do we compare the size of nodes when inserting? There is no problem with set. You can directly compare with T, but not map. We need to take out the first of pair < >. This is to implement an imitation function.
The imitation function overloads the operator(), and this class can be used like a function.
template<class K, class V>
class map
{
struct MapKeyOfT
{
const K& operator()(const pair<const K, V>& kv)
{
return kv.first;
}
};
private:
RBTree<K,pair<const K, V>, MapKeyOfT> _t;
};
}
However, the underlying red black tree does not know whether it is Key or pair < >, so the red black tree will obtain the Key value through the imitation function for comparison. Therefore, set also needs to add an imitation function. It seems superfluous for set, but the red black tree at the bottom doesn't know, so imitation function is essential.
template<class K>
class set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
private:
RBTree<K, K, SetKeyOfT> _t;
};
}
The input of set into the bottom layer is the imitation function of set, and the input of map into the bottom layer is the imitation function of map.
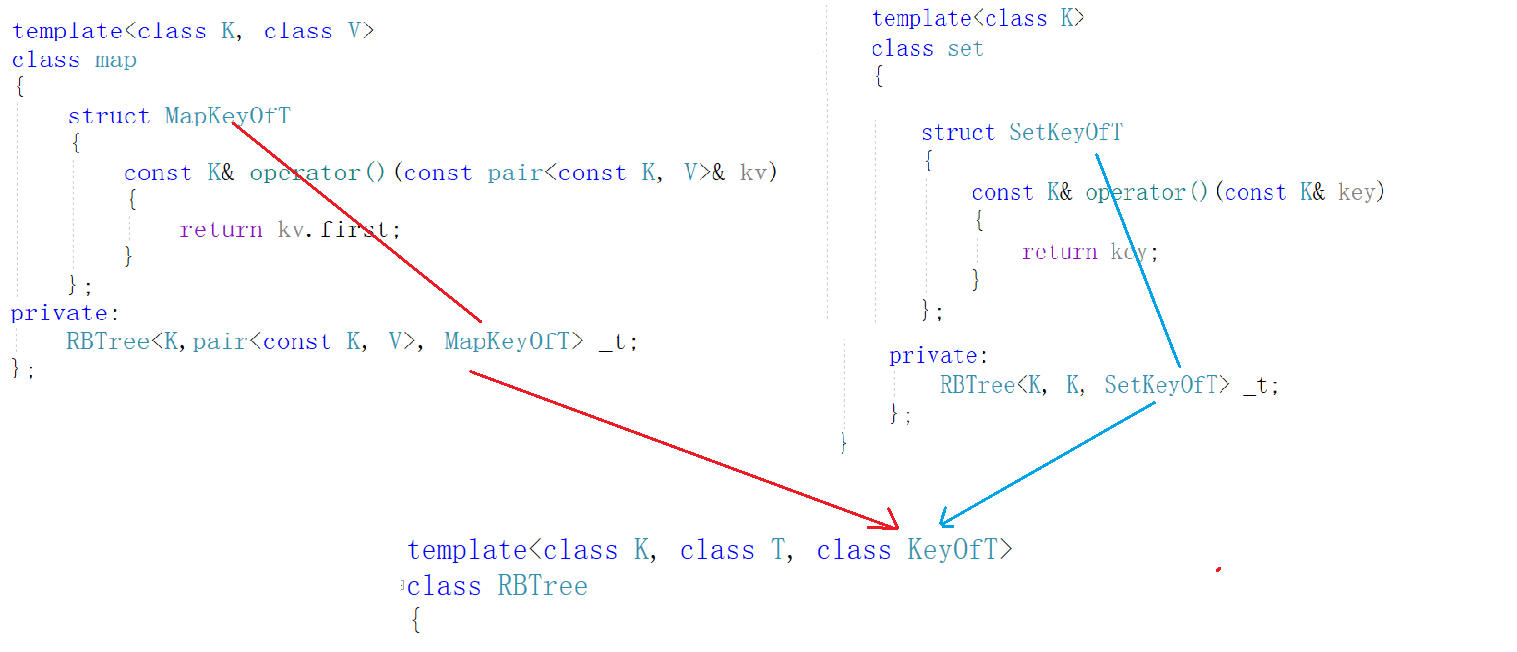
Implementation of forward iterator
The iterator encapsulates the pointer of a node, and there is only one member variable, that is, the pointer of the node.
template<class T,class Ref,class Ptr>
struct _TreeIterator
{
typedef RBTreeNode<T> Node;//Type of node
typedef _TreeIterator<T, Ref, Ptr> Self;//Type of forward iterator
Node* _node;//Encapsulated pointer
};
So we can construct an iterator through the pointer of a node
//Constructor
_TreeIterator(Node* node)
:_node(node)
{}
When the iterator dereferences, we return a reference to the node data
Ref operator*()
{
return _node->_data;
}
When the iterator performs the - > operation, we return the pointer of the node data
Ptr operator->()
{
return &_node->_data;
}
You also need to implement = = and= To determine whether the node is the same.
bool operator !=(const Self& s) const
{
return _node != s._node;
}
bool operator ==(const Self& s) const
{
return _node == s._node;
}
operator++
The main play is to implement + +.
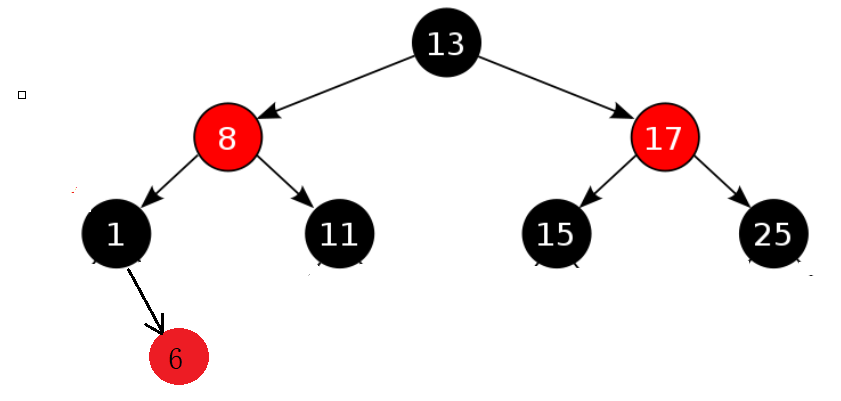
begin and end of iterators in red black tree:
- begin returns the iterator of the first node in the middle order, which is the leftmost node
- end returns the iterator at the next position of the last node in the middle order. Here, use a null pointer.
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
RBTree()
:_root(nullptr)
{}
typedef _TreeIterator<T, T&, T*> iterator;
iterator begin()
{
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);
}
iterator end()
{
return iterator(nullptr);
}
private:
Node* _root;
};
We use + + to find the next node in the middle order. The specific logic is as follows:
1. If the right subtree of the current node is not empty, + + must find the leftmost node of the right subtree
2. If the right subtree of the current node is empty, + + you need to find the ancestor whose child is not on the right of the father
Self& operator++()
{
if (_node->_right)
{
// The next access is the first node in the middle order in the right tree
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left;//++Then it becomes the node
}
else //The right subtree is empty
{
//Find an ancestor whose child is not on the father's right
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;//++Then it becomes the node
}
return *this;
}
operator–
After the forward iterator of a node is -- operated, it is the previous node of the node found by sequential traversal in the red black tree. That is, the opposite of + +.
The specific logic is as follows:
1. The left subtree of the current node is not empty, - find the rightmost node in the left subtree
2. The left subtree of the current node is empty, -- find the ancestor whose child is not on the left of the father
Self& operator--()
{
if (_node->_left)
{
// The next access is the first node in the middle order in the right tree
Node* left = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = right;
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Encapsulated set and map
Code for set
Next, you can directly call the insertion of the red black tree to find it. The blogger did not delete the red black tree.
namespace p
{
template<class K>
class set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K, K, SetKeyOfT> ::iterator iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
//insert
bool insert(const K& k)
{
_t.insert(k);
return true;
}
//lookup
iterator find(const K& k)
{
return _t.Find(key);
}
private:
RBTree<K, K, SetKeyOfT> _t;
};
}
map code
namespace g
{
template<class K, class V>
class map
{
struct MapKeyOfT
{
const K& operator()(const pair<const K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
//insert
pair<iterator,bool> insert(const pair<const K, V>& kv)
{
return _t.insert(kv);
}
//operator[]
V& operator[](const K& key)
{
pair<iterator, bool> ret = Insert(make_pair(key, V()));
iterator it = ret.first;
return it->second;
}
//lookup
iterator find(const K& k)
{
return _t.Find(key);
}
private:
RBTree<K,pair<const K, V>, MapKeyOfT> _t;
};
}
The encapsulated red black tree code can be clicked
Test iterators for set and map
Bloggers here only test iterators
void Test_set()
{
p::set<int> s;
s.insert(1);
s.insert(10);
s.insert(5);
s.insert(20);
s.insert(1);
p::set<int>::iterator it = s.begin();
while (it != s.end())
{
cout << *it << " ";
++it;
}
cout << endl;
}
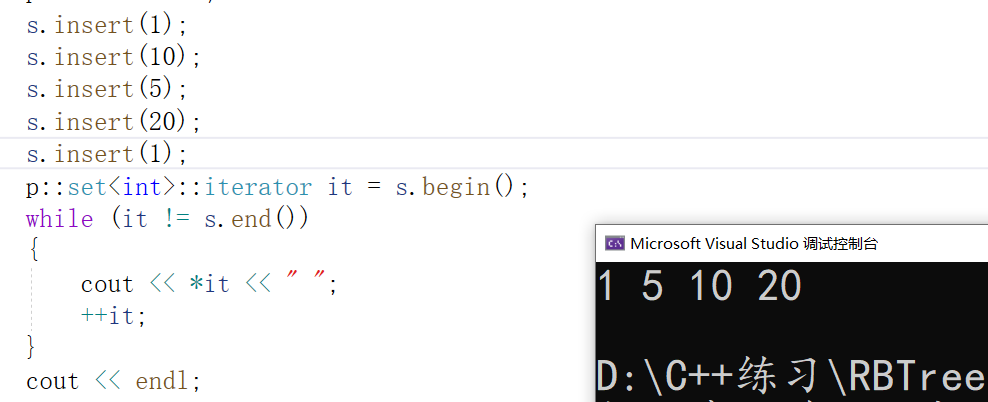
Iterator test for map:
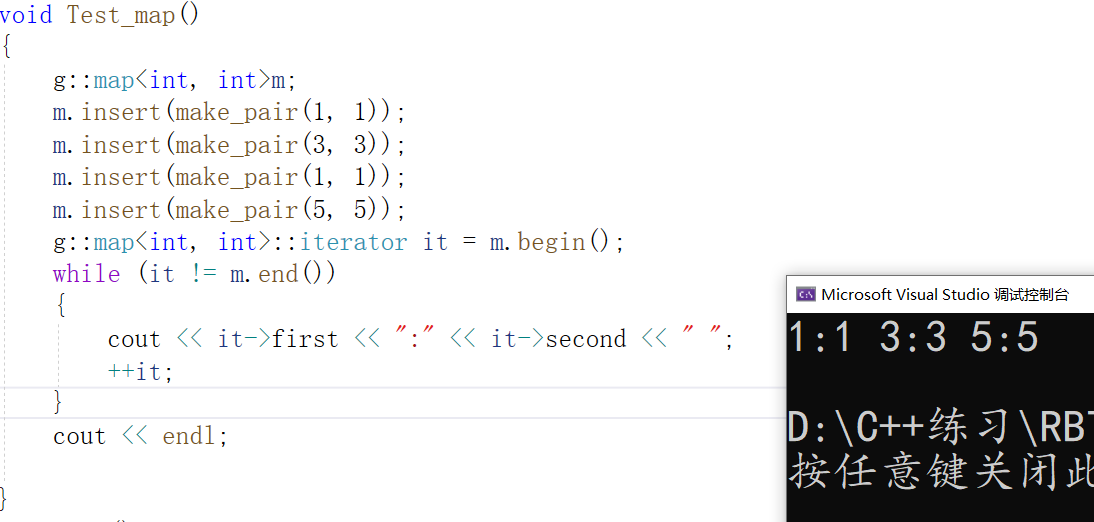
The simulation implementation does not need to make its own wheels. It can know the underlying structure better and be handy when using it in the future. This blog is over.