preface

This article uses three examples to explain the single adjustment stack

What is a monotone stack

The elements in the stack are strictly or non strictly monotonically increasing or decreasing
When implementing, maintain the order of elements in the stack

Example 1 Acwing1978 (simple)

Title Link https://www.acwing.com/problem/content/description/1980/

subject

Every day, farmer John's N cows cross the road in the middle of the farm. Consider the two-dimensional map of John's farm. The road extends horizontally. One side of the road is described by line y=0 and the other side by line y=1. Cow i crosses the road in a straight line from the position on one side of the road (ai,0) to the position on the other side (bi,1).
All ai are different from each other, and all bi are different from each other.
Despite the agility of his cows, he was worried that the two cows crossing the action path would collide when crossing the road.
John believes that a cow is safe if its path of action does not intersect with that of any other cow.
Please help John calculate the number of safe cows.

Input format
The first line contains the integer N.
Next, N lines, each containing two integers AI and Bi, are used to describe the action path of a cow.

Output format
Output the number of safe cows.

Data range
1 ≤ N ≤ 1 0 5 , − 1 0 6 ≤ a i , b i ≤ 1 0 6 1≤N≤10^5,−10^6≤a_i,b_i≤10^6 1≤N≤105,−106≤ai​,bi​≤106

sample input

4
-3 4
7 8
10 16
3 9

sample output

2

Example explanation

The routes of the first cow and the third cow do not intersect with the routes of other cows.
The course of action of the second cow and the fourth cow intersect.

Topic analysis

The algorithm of monotone stack (strictly monotone increasing stack) is used after sorting:

1. If the newly added element is larger than the maximum value, it can be added
2. If the newly added elements are smaller than the maximum value, there may be intersection, and the monotonic increment of the stack is maintained by deleting the elements in the stack

code

#include <bits/stdc++.h>

using namespace std;
struct Node
{
    int x;
    int y;
};

bool cmp(Node &p1, Node &p2)
{
    return p1.x < p2.x;
}

int main()
{
    int n; cin >> n;
    Node a[n];
    for (int i = 0; i < n; i ++ ) scanf("%d%d", &a[i].x, &a[i].y);
    sort(a, a + n, cmp); //Sort by x from small to large, and the stacked element is y
    
    stack<int> sta; //Monotone strictly increasing stack
    int maxn = -1e7;
    for(int i = 0; i < n; ++ i)
    {
        if(maxn < a[i].y) sta.push(a[i].y);  //The new one won't intersect with the original one
        else
            while(sta.size() && sta.top() > a[i].y) //Otherwise, there may be intersection, and all intersecting parts may be cleared
                sta.pop();
        maxn = max(maxn, a[i].y); //Maximum value per update
    }
    
    cout << sta.size();
    return 0;
}

Example 2 force buckle 402 (medium)

Title Link https://leetcode-cn.com/problems/remove-k-digits/

subject

Give you a non negative integer num represented by a string and an integer k. remove the k digits in this number to minimize the remaining numbers. Please return the smallest number as a string.

Example 1:

Input: num = "1432219", k = 3
Output: "1219"
Explanation: remove the three numbers 4, 3, and 2 to form a new minimum number 1219.

Example 2:

Input: num = "10200", k = 1
Output: "200"
Explanation: remove the first 1 and the remaining number is 200 Note that the output cannot have any leading zeros.

Example 3:

Input: num = "10", k = 2
Output: '0'
Explanation: remove all numbers from the original number. If the rest is empty, it is 0.

Tips:

1 <= k <= num.length <= 105
num Only a few digits (0) - 9)form
 In addition to 0 itself, num Without any leading zeros

Topic analysis

An intuitive idea is to delete the large numbers that appear in the front. Is a monotonous idea. The right side of the string is regarded as the opening of the stack, and the left side of the string is closed.

Improve the details around this core:

1. When adding a number in advance, delete the larger one in front of it, delete one, and reduce the total number of times
2. With leading zeros: clear
3. After the last traversal, the total number of possible times of the next task has not been reduced to 0, and it is deleted from the back to the front
4. Finally, if it is empty, return 0

code

class Solution {
public:
    string removeKdigits(string num, int k) {
        //Ascending order
        int n = num.size();
        string s;  //Abstract the string into a stack. The bottom of the stack is on the left and the top of the stack with an opening is on the right
        for(int i = 0; i < n; ++ i)
        {
            //The core idea is to delete the large numbers that appear in the front
            while(k && s.size() && s.back() > num[i]) s.pop_back(), k --; //Total times of each reduction
            if(s == "0") s = ""; //Remove prefix 0
            s.push_back(num[i]); //Add current to answer
        }
        while(k && s.size()) s.pop_back(), k--;  //At this time, the stack is non strictly monotonically increasing and deleting from back to front
        if(!s.size()) return "0"; //Special judgment
        return s;
    }
};

Example: three force deduction 84 (difficult)

Title Link https://leetcode-cn.com/problems/largest-rectangle-in-histogram/

subject

Give n non negative integers to represent the height of each column in the histogram. Each column is adjacent to each other and has a width of 1.

Find the maximum area of the rectangle that can be outlined in the histogram.

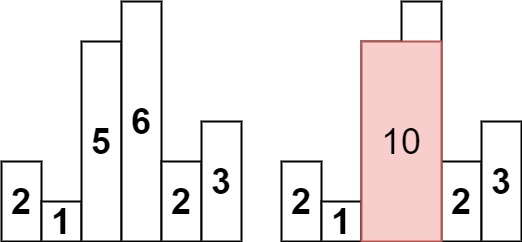
Input: heights = [2,1,5,6,2,3]
Output: 10
 Explanation: the largest rectangle is the red area in the figure, with an area of 10

Data range

• $ 1 <= heights.length <=10^5 $
• 0 < = h e i g h t s [ i ] < = 1 0 4 0 <= heights[i] <= 10^4 0<=heights[i]<=104

Topic analysis

The violent method is to enumerate each point, traverse the point to both sides of the double pointer, and terminate the double pointer traversal when encountering elements smaller than it. However, in extreme cases, the time complexity of this practice is as high as O ( n 2 ) O(n^2) O(n2) is an algorithm with worrying efficiency.

What are the characteristics of stack? First in, then out. In the process of traversing from left to right, each possible point looks for the answer to the left, which is in line with the characteristics of the stack.

The core idea is to maintain a non strictly monotonically increasing stack during right traversal. When the answer cannot be determined, the subscript will be put on the stack, and all unnecessary data will be out of the stack when the answer can be determined.

Some details:

1. Stack only saves Subscripts

2. Finally, a number smaller than all the numbers should be put into the stack to empty the stack

3. With a little greedy strategy: if the original stack is 134 134 134, to be put into the stack 2 2 2， 3 3 3 and 4 4 4 after that, the maximum height can only reach 2 2 2. Update the height of the original array

code

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        heights.push_back(-1);  //Make sure that the stack is empty at the end
        int n = heights.size();
        stack<int> sta;
        int ans = 0, tmp;
        for(int i = 0; i < n; ++ i)
        {
            if(sta.empty() || heights[i] >= heights[sta.top()]) sta.push(i); //Unable to determine the answer, put it on the stack first
            else // I can confirm the answer
            {
                int idx;
                while(sta.size() && heights[i] < heights[sta.top()]) //Non strictly monotonic increment of maintenance stack
                {
                    idx = sta.top();
                    sta.pop();
                    ans = max(ans, heights[idx] * (i - idx)); //Update answer
                }
                sta.push(idx); //Put the to be put into the stack
                heights[idx] = heights[i]; //Changing the data size of the original array can only be so high
            }
        }
        return ans;
    }
};

summary

The core of monotone stack is to maintain the order of data in the stack. Directly enter the stack on the premise of order; If you are not satisfied, you can achieve order by deleting the data in the stack.

The pseudo code is roughly:

for(int i = 0; i < n; ++ i)  //Go through it from left to right
{
    if(sta.empty() || f1) sta.push(i); //The direct stack f1 satisfies a certain condition   
    else //Otherwise, maintain the order of elements in the stack
    {
        while(sta.size() && f2) //Delete it as long as it can't be orderly
        {
            sta.pop(); //Satisfy the order in the stack by deleting
            x1; //Other statements executed
        }
    }
    x2; //Write according to the requirements of the topic
}