Using Pb in Prim algorithm_ DS heap optimization

Prim algorithm is used to find the Minimum Spanning Tree (MST). Its essence is a greedy addition method. For an undirected graph with interconnected points, the specific steps of prim algorithm are as follows:

Let \ (G=(V,E) \) represent the original drawing, \ (G'=(V',E ') \) represent the minimum spanning tree of \ (g \), and \ (dis_ \) represent the minimum distance from node \ (u \) to any \ (v \in V' \) (initialized as \ (\ infty \).

1. Take any node \ (s \in V \), and make \ (dis_s=0 \);
2. Find a node \ (U \ in \ completion_v '\) to minimize \ (dis_u u \);
3. Add \ (U \) to \ (V '\), and add \ (E' \) to the edge represented by \ (dis_u \);
4. For any edge \ ((u,v) \ in \ complexity_ E '\), let \ (dis_v=\min \{dis_v,w \} \), where \ (w \) is the weight of edge \ ((u,v) \);
5. Repeat procedure 2 through procedure 4 until \ (V'=V \).

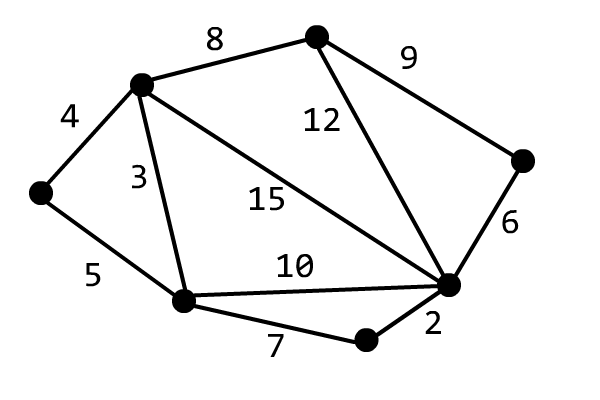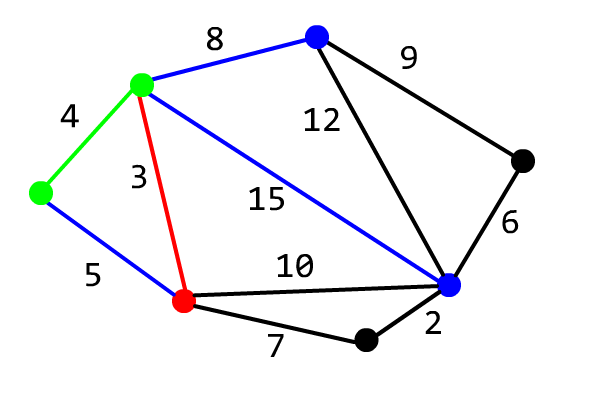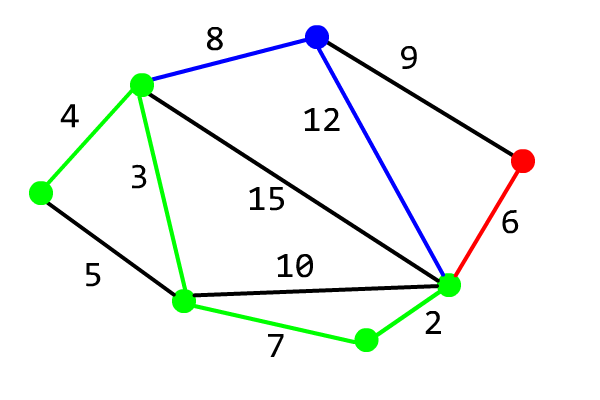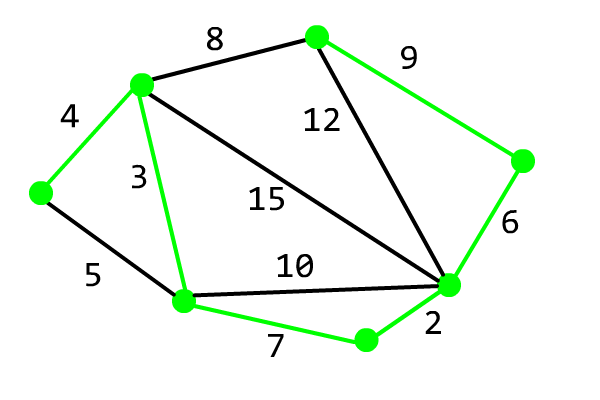
The correctness of the algorithm can be used for reference OI Wiki.

The time complexity of the simple Prim algorithm is \ (O(n^2+m) \), most of which is consumed in operation 2. It can be optimized by heap. The optimized time complexity of binary heap and other heaps that do not support \ (O (1) \) decrease key operation is \ (O((n+m)\log n) \), and the optimized time complexity of Fibonacci heap is \ (O(n \log n+m) \) (Reference) OI Wiki ). Compared with Kruskal algorithm, Prim algorithm is more efficient on dense graphs.

The decrease key operation is widely used in Prim algorithm. In OI competition, in order to save time, the encapsulated data structure in C + + standard library can be used to replace the handwriting heap. Due to std::priority_queue does not support decrease key operation and is often replaced by std::map. In fact, the internal implementation of std::set is a red black tree with a large constant. This usage will obviously affect the operation efficiency. In view of the fact that the GNU compiler is almost used in the current oi competition, and CCF has explicitly allowed the use of pb_ds , we can use__ gnu_pbds::priority_queue is used as the heap to optimize the Prim algorithm. Different types of heap can be selected as the internal implementation. The fastest and default is Pairing Heap. See code template for specific usage( P3366 [template] minimum spanning tree - Luogu):

#include <bits/extc++.h>

using namespace std;
const int maxn = 5005;
const int inf = 0x3f3f3f3f;
int n, m;
vector<pair<int, int>> g[maxn];
__gnu_pbds::priority_queue<pair<int, int>, greater<>> heap;
__gnu_pbds::priority_queue<pair<int, int>, greater<>>::point_iterator p[maxn];  // dis[i] and iterator for decrease-key

int prim() {
    int ans = 0;
    p[1] = heap.push(make_pair(0, 1));
    for (int i = 2; i <= n; ++i)
        p[i] = heap.push(make_pair(inf, i));
    while (!heap.empty()) {
        if (heap.top().first == inf)
            return -1;
        int u = heap.top().second;
        ans += heap.top().first;
        heap.pop();
        p[u] = heap.end();
        for (auto& i : g[u])
            if (p[i.first] != heap.end() && i.second < p[i.first]->first)
                heap.modify(p[i.first], make_pair(i.second, i.first));
    }
    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    for (int i = 1; i <= m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        g[u].emplace_back(v, w);
        g[v].emplace_back(u, w);
    }
    int ans = prim();
    if (ans != -1)
        cout << ans << endl;
    else
        cout << "orz" << endl;
    return 0;
}

Please indicate the source of reprint. Original address: https://www.cnblogs.com/na-sr/p/clang-format.html