n sprinklers are installed in a horizontal strip of grass l meters long and w meters wide. Each sprinkler is installed at the horizontal center line of the strip. For each sprinkler we are given its position as the distance from the left end of the center line and its radius of operation.
What is the minimum number of sprinklers to turn on in order to water the entire strip of grass?
Input
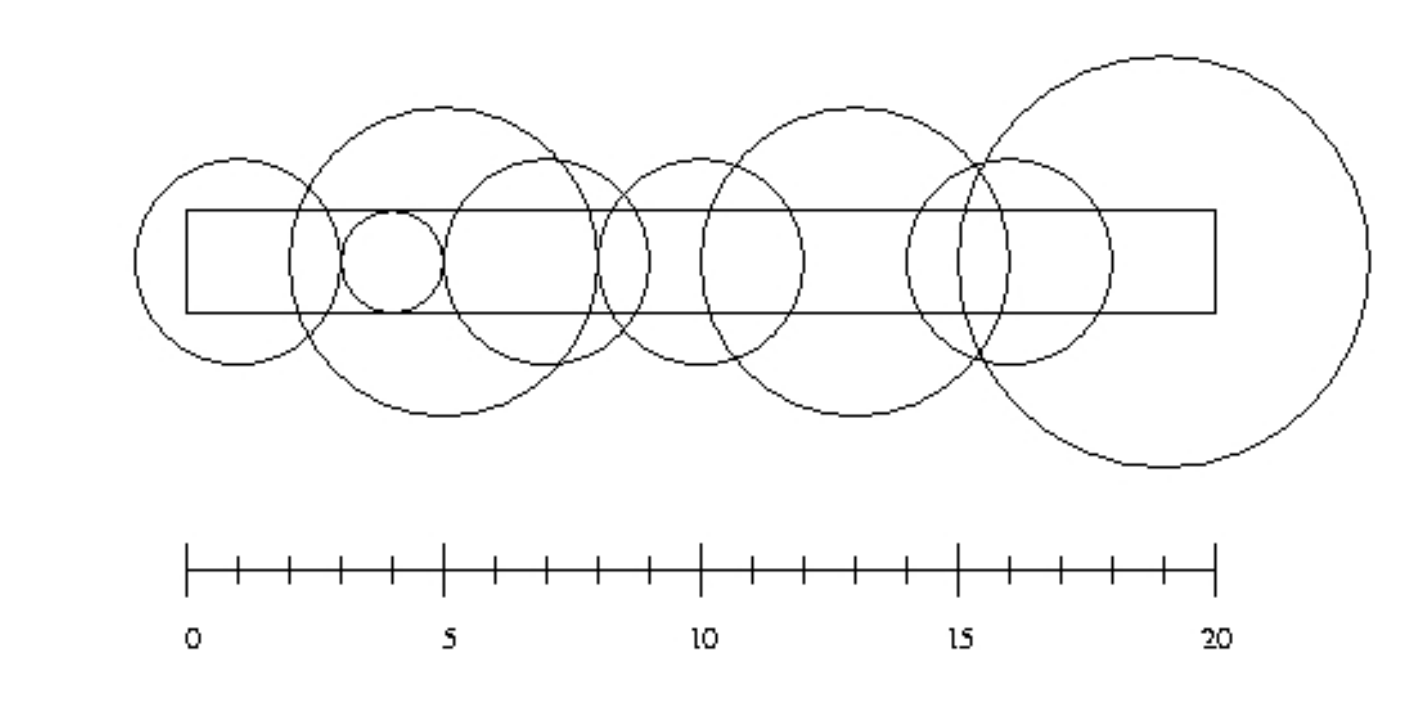
Input consists of a number of cases. The first line for each case contains integer numbers n, l and w with n ≤ 10000. The next n lines contain two integers giving the position of a sprinkler and its radius of operation. (The picture above illustrates the first case from the sample input.)
Output
For each test case output the minimum number of sprinklers needed to water the entire strip of grass. If it is impossible to water the entire strip output '-1'.

Topic: Give you n sprinklers their length and width, then give their center and radius, and ask how many sprinklers you need at least to cover the whole grass.
Ideas: Use the Pythagorean Theorem to find the end points of left and right intervals that each device can reach and exist in the structure, sort them (left interval from small to large, right interval from large to small), and finally convert them to the problem of interval coverage.
Special judgment:
- The left endpoint of the first interval after sorting needs to be less than or equal to 0, and the maximum right endpoint needs to be greater than or equal to the length of the sketch
- Consider that the left endpoint of the next interval is less than or equal to the right endpoint of the current interval, but its right endpoint is less than or equal to the right interval of the point.
- Marked with flag, if an intermediate break occurs during traversal, that is, the left end of the next interval is larger than the current maximum right interval
Given the 7-15, 13-17, 15-20 scenarios, it's easy to count the second one. Originally, variables were used to record the longest distance, and then to update the distance and coordinates of variables, which ended with a for loop. However, it was found that doing so could be overwhelming on the test data, and whi was needed to stop the loop anytime, anywhere.Le loop to write.
AC:
1 #include<iostream> 2 #include<math.h> 3 #include<stdio.h> 4 #include<algorithm> 5 #define inf 0x3f3f3f3f 6 using namespace std; 7 8 struct node 9 { 10 double l; 11 double r; 12 } a[10020]; 13 14 int cmp1(node x,node y) 15 { 16 if(x.l!=y.l) 17 return x.l<y.l; 18 else 19 return x.r>y.r; 20 21 } 22 //Sort left boundary coordinates from smallest to largest,//Why doesn't the right endpoint need to be sorted 23 24 25 int main() 26 { 27 std::ios::sync_with_stdio(false); 28 int n; 29 double len,w; 30 double c,rr; 31 while(cin>>n>>len>>w) 32 { 33 int num=0; 34 double maxxr=-1.0; 35 for(int i=0; i<n; i++) 36 { 37 cin>>c>>rr; 38 if(rr*2<=w) 39 { 40 continue; 41 } 42 else 43 { 44 double l=c-sqrt(rr*rr-w*w/4); 45 double r=c+sqrt(rr*rr-w*w/4); 46 // printf("%lf--%lf\n",l,r); 47 if(r>=maxxr) 48 { 49 maxxr=max(maxxr,r); 50 } 51 // if(l<=0) 52 // l=0; 53 a[num].l=l; 54 a[num++].r=r; 55 } 56 } 57 sort(a,a+num,cmp1); 58 int k=0; 59 if(a[0].l>0||maxxr<len) 60 { 61 cout<<-1<<endl; 62 continue; 63 } 64 double maxx=0; 65 int ans=0; 66 int flag=0; 67 int ww=0; 68 while(maxx<len) 69 { 70 double uu=maxx; 71 for(int i=0; i<num; i++) 72 { 73 if(a[i].l<=uu&&a[i].r>maxx) 74 { 75 // minn=a[i].l; 76 maxx=a[i].r; 77 // zz=i; 78 } 79 } 80 // printf("%lf----%d\n",maxx,zz); 81 if(uu==maxx&&uu<len) 82 { 83 ww=1;break; 84 } 85 //minn=a[zz].l; 86 ans++; 87 /*for(int i=0; i<num; i++) 88 { 89 //printf("%lf*****%lf\n",a[i].l,a[i].r); 90 if(a[i].l<=maxx) 91 { 92 if(a[i].r>maxx) 93 { 94 maxx=a[i].r; 95 ans++; 96 printf("%lf----%lf\n",a[i].l,a[i].r); 97 } 98 else 99 { 100 continue; 101 } 102 } 103 if(a[i].l>maxx) 104 { 105 flag=0; 106 break; 107 } 108 if(a[i].r>=len) 109 { 110 flag=1; 111 break; 112 }*/ 113 //}//If the middle part cannot be connected, process: flag sign 114 } 115 // printf("%d\n",ans); 116 if(ww==0) 117 cout<<ans<<endl; 118 else 119 cout<<-1<<endl; 120 } 121 return 0; 122 }
With the for loop code, the code is wrong, but with this idea
1 #include<iostream> 2 #include<math.h> 3 #include<stdio.h> 4 #include<algorithm> 5 #define inf 0x3f3f3f3f 6 using namespace std; 7 8 struct node 9 { 10 double l; 11 double r; 12 } a[10020]; 13 14 int cmp1(node x,node y) 15 { 16 if(x.l!=y.l) 17 return x.l<y.l; 18 else 19 return x.r>y.r; 20 21 } 22 //Sort left boundary coordinates from smallest to largest 23 24 25 int main() 26 { 27 //std::ios::sync_with_stdio(false); 28 int n; 29 double len,w; 30 double c,rr; 31 while(cin>>n>>len>>w) 32 { 33 int num=0; 34 double maxxr=-1.0; 35 for(int i=0; i<n; i++) 36 { 37 cin>>c>>rr; 38 if(rr*2<=w) 39 { 40 continue; 41 } 42 else 43 { 44 double l=c-sqrt(rr*rr-w*w/4); 45 double r=c+sqrt(rr*rr-w*w/4); 46 // printf("%lf--%lf\n",l,r); 47 if(r>=maxxr) 48 { 49 maxxr=max(maxxr,r); 50 } 51 // if(l<=0) 52 // l=0; 53 a[num].l=l; 54 a[num++].r=r; 55 } 56 } 57 sort(a,a+num,cmp1); 58 int k=0; 59 int pp=0; 60 if(a[0].l>0||maxxr<len) 61 { 62 cout<<-1<<endl; 63 continue; 64 } 65 double maxx=0; 66 double minn=0; 67 int ans=0; 68 int flag=0; 69 int w=0; 70 int ww=0; 71 int d=0; 72 int z=0; 73 int qq=0; 74 for(int i=0; i<num; i=qq) 75 { 76 //printf("%lf*****%lf\n",a[i].l,a[i].r); 77 if(a[i].l<=maxx) 78 { 79 if(a[i].r>maxx) 80 { 81 if(maxx>=len) 82 { 83 printf("%d\n",ans); 84 pp=1; 85 } 86 w=i; 87 ww=a[i].r-a[i].l; 88 // maxx=a[i].r; 89 // ans++; 90 // printf("%lf----%lf\n",a[i].l,a[i].r); 91 for(int j=i+1;j<num;j++) 92 { 93 z=a[j].r-a[j].l; 94 if(a[j].l<=maxx&&a[j].r>maxx) 95 { 96 if(z>ww) 97 { 98 w=z; 99 } 100 } 101 if(a[j].l>maxx) 102 break; 103 } 104 // printf("%lf----%lf\n",a[i].l,a[i].r); 105 maxx=a[w].r; 106 qq=w; 107 printf("%lf\n",maxx); 108 w=0; 109 ans++; 110 if(maxx>=len) 111 { 112 printf("%d\n",ans); 113 pp=1; 114 } 115 printf("%d\n",ans); 116 if(pp==1) 117 break; 118 } 119 else 120 { 121 continue; 122 } 123 if(pp==1) 124 break; 125 } 126 127 // if(a[i].l>maxx) 128 // { 129 // flag=0; 130 // break; 131 // } 132 // if(a[i].r>=len) 133 // { 134 // flag=1; 135 // break; 136 // } 137 } 138 // printf("%d\n",ans); 139 140 141 // if(flag) 142 /*if(maxx>=len) 143 cout<<ans<<endl; 144 */ 145 if(pp==0) 146 cout<<-1<<endl; 147 } 148 return 0; 149 }