link

0x00 train of thought

Look at the questions first.
Given a system composed of dominoes, calculate when and where the last dominoes fall. When a key domino falls, all dominoes connected to the key domino begin to fall (except those that have fallen). When the fallen dominoes reach other key dominoes that have not yet fallen, these key dominoes will also fall and cause the dominoes connected to them to begin to fall. Dominoes may fall from either end. It is even possible for the same domino row to fall from both ends, in which case the last domino of the row to fall is located between the key dominoes at both ends of the row. You can assume that the dominoes in the row fall at a uniform speed (i.e. 1s).

Still can't understand? Try this:
About the domino game, there are n key dominoes, and there is a line of ordinary dominoes between the key dominoes. Tell you how long it takes for a row of dominoes to fall between key dominoes. At the beginning, push down the key dominoes numbered 1 and ask you when and where the last dominoes fell. (if two adjacent key dominoes can fall at the same time, the middle dominoes fall after the two key dominoes).

At first, I saw that there was actually no idea about the problem. Let's analyze the sample:

3 3
1 2 5
1 3 5
2 3 5

Hiss... This input... Is a bit like a picture. Let's try to understand it as a picture?

n/*point*/ m/*Number of sides*/
u/*starting point*/ v/*End*/ w/*Weight */
//Undirected edge

Very smooth.
Our problem is to find the point / edge with the largest weight.

Then, since the starting point is fixed (1), you only need to make a single source shortest circuit, and the point will be processed.

Next look.
It is known that there can be an ordinary dominoes between these two key dominoes.
Because we can arbitrarily place ordinary dominoes between two key dominoes, we can roughly understand that there are countless ordinary dominoes between two key dominoes, and the time when these ordinary dominoes fall is the time when the last ordinary dominoes between the two key dominoes fall.
The last dominoes we can find between these two key dominoes must be $\ dfrac{u+v+w}{2} $(put the proof at the end). Just find it violently.

After knowing this, we can write a mature code.

But before that

0x01 attention

Please take a closer look at the output format and sample output!!!!!!

First, multiple groups of input and output.

Second, don't forget to output a blank line after each group of data.

Third, pay attention to:

System #1

The last domino falls after 27.0 seconds, at key domino 2.

System #2

The last domino falls after 7.5 seconds, between key dominoes 2 and 3.

Fourth, the key dominoes on both sides of ordinary dominoes are output in ascending order.


Lessons of blood and tears QAQ

code

#include<bits/stdc++.h>
using namespace std;
int n,m,eat,times,d[100005];
bool b[100005];
typedef struct _dianquan
{
    int to,times;
}E;
bool operator<(const _dianquan& a,const _dianquan& b)
{
    return a.times>b.times;
}
E t1,t2;
int G[505][505];
void bl(int first)//Single source shortest circuit
{
    //Empty array+initialization
    memset(d,0x3f,sizeof(d));
    memset(b,0,sizeof(b));
    d[first]=0;
    priority_queue<E>q;
    b[first]=1;
    t1.to=first;
    t1.times=0;
    q.push(t1);
    
    //Start slack operation
    int i;
    while(!q.empty())
    {
        int now=q.top().to;
        q.pop();
        b[now]=0;
        for(i=1;i<=n;i++)
        {
            if(G[now][i]<G[0][0]&&d[i]>d[now]+G[now][i])
            {
                d[i]=d[now]+G[now][i];
                if(!b[i])
                {
                    b[i]=1;
                    t1.to=i;
                    t1.times=G[now][i];
                    q.push(t1);
                }
            }
        }
    }
}
int main()
{
    int i,j,first,t=0,u,v,w;
    while(scanf("%d %d",&n,&m)!=EOF&&n)//Multiple input and output groups
    {
        t++;
        memset(G,0x3f,sizeof(G));
        for(i=1;i<=n;i++)
            G[i][i]=0;
        for(i=0;i<m;i++)
        {
            scanf("%d %d %d",&u,&v,&w);
            G[u][v]=G[v][u]=w;
        }
        bl(1);
        double keymax=0;
        int keywhere=1;
        for(i=1;i<=n;i++)//The last key dominoes to fall
        {
            if(d[i]>keymax)
            {
                keymax=d[i];
                keywhere=i;
            }
        }
        double unkeymax=0;
        int unkey_little=0,unkey_bigger=0;
        for(i=1;i<=n;i++)//The last ordinary dominoes to fall
        {
            for(j=i+1;j<=n;j++)
            {
                if((d[i]+d[j]+G[i][j])/2.0>unkeymax&&G[i][j]<G[0][0])
                {
                    unkeymax=(d[i]+d[j]+G[i][j])/2.0;
                    unkey_little=i;
                    unkey_bigger=j;
                }
            }
        }
        printf("System #%d\n",t);
        if(keymax>=unkeymax)//As for why>=，See case 2 below for details
            printf("The last domino falls after %.1lf seconds, at key domino %d.\n\n",keymax,keywhere);
        else
            printf("The last domino falls after %.1lf seconds, between key dominoes %d and %d.\n\n",unkeymax,unkey_little,unkey_bigger);
    }
    return 0;
}

0x02 certificate

There are only two cases for either edge.

1. This side cannot make any key dominoes on the left and right sides fall (that is, the key dominoes on the left and right sides make the dominoes on this side fall).

Let's look at the pattern diagram: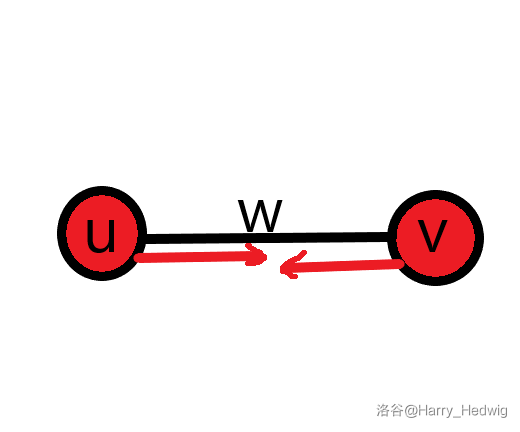


As we all know, dominoes fall when touched, which is why the works of art made with them are very short-lived. Therefore, on the line segment with length w, the point where the left endpoint meets the right endpoint finally falls. (let u ≤ v) and the falling time of this point is

$$v+[w-(v-u)\times 1]\div 2=v+\dfrac{w-v+u}{2}=\dfrac{u+v+w}{2}$$

Get a certificate.
2. When the key dominoes on one side fall, the other key dominoes will fall faster due to the existence of this side.
Let's also take a look (assuming u falls first):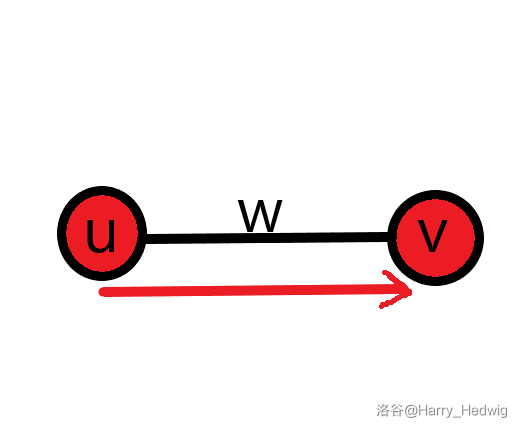



Then we can get v=u+w, and in this case $\ dfrac{u+v+w}{2}=\dfrac{2(u+w)}{2}=u+w=v $, that is, the ordinary dominoes are at the key dominoes. Therefore, in order to prevent such errors, we can give priority to the key dominoes (i.e. in the code)

if(keymax>=unkeymax)

)Then ordinary dominoes.

So far, the situation has been considered, and then the problem solution should be over. I'll see you next time!