preface
We have introduced the logical volume manager LVM before. Its main function is to scale the file system, so that people can use disk space more flexibly. However, the emergence of LVM can not solve the problem of data optimization. There are often some duplicate data or empty blocks on our devices, which will greatly waste our disk space. How to solve these problems? This is about to use the virtual data optimizer VDO, our protagonist today
1. What is VDO?
VDO is Virtual Data Optimize, which is called virtual data optimizer in Chinese. It can optimize storage space by compressing or deleting data on the device.
VDO is generally placed on the top of existing block storage devices (such as local disks) and works in three stages, so as to reduce the occupied space on the storage devices.
- Exclusion of zero blocks
- Delete duplicate data
- compressed data
2. Establish VDO equipment
Key points of installing VDO: VDO devices must be installed on a new disk. Of course, if your disk is not a new disk, you can also obtain a new disk through initialization.
The commands used in this part are as follows:
dd if=/dev/zero of=/dev/vdb bs=1M count=1 Function: initialize disk dnf install vdo -y install vdo vdo create --name=mars_vdo1 --device=/dev/vdb Will equipment/dev/vdb Create a file named mars_vdo1 of vdo vdo status --name=mars_vdo1 |less use less Turn the page to read the name mars_vdo1 of vdo functional status
The specific operations are as follows:

Create a vdo and use less to turn pages to read the status of related functions. You can mainly check the two functions of the vdo: delete duplicate data and whether data compression is on. The details are as follows:
 When the functions of duplication and Compression are enabled, the function is turned on.
When the functions of duplication and Compression are enabled, the function is turned on.
3. Mounting and use of VDO equipment
After creating vdo, it will not start working automatically. We also need to initialize the vdo device and mount it in an empty directory to enable vdo to start its data optimization.
The commands used in this section are as follows:
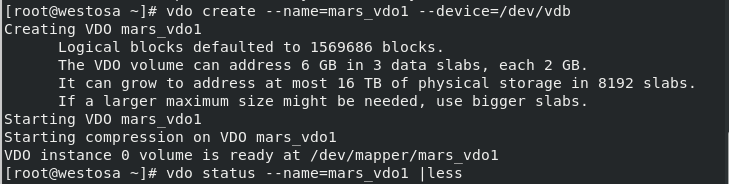
mkfs.xfs -K /dev/mapper/mars_vdo1 initialization vdo mkdir /mars_vdo Create one that can be used for mounting vdo Empty directory for mount /dev/mapper/mars_vdo1 /mars_vdo/ mount vdo
The specific operations are as follows:
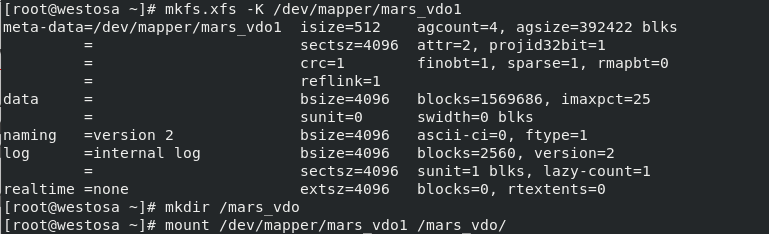 After initialization and mounting, we can use vdo. Here, we also have several commands about vdo devices as follows:
After initialization and mounting, we can use vdo. Here, we also have several commands about vdo devices as follows:
vdo stop --name Equipment name close VDO equipment vdo start --name Equipment name open VDO equipment vdo remove --name Equipment name delete VDO equipment
4. Test vdo
We can use vdo above. Next, let's see the charm of vdo.
The basic idea is: after mounting vdo, we create a duplicate file or a blank file with the same content as a file in vdo, and then detect the utilization of our device storage before and after the file is created. In order to make the test effect more obvious, we need a large file as the experimental material. If it is difficult to find a large file in your host, you can use the following operations:
Commands used to create material:
touch big Create an empty file dd if=/dev/zero of=big bs=1M count=1024 Use 1 G The blank area overwrites the file to get 1 G Empty file ls -l big history >> big take history Append content to file ls -l big
The specific operations are as follows:


With this big file material, we can finally start our test.
The commands used in the test are as follows:
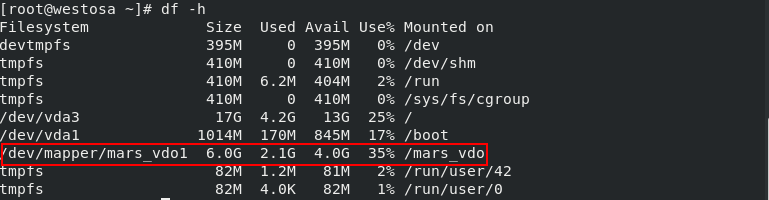
df -h /mars_vdo/ View mount status vdostats --human-readable read vdo Storage condition cp big /mars_vdo/big1 Copy large files vdostats --human-readable Read again vdo Storage condition
The operation process is as follows:


We can find that even if the big file is stored in Mars_ In vdo, the storage occupancy of the vdo does not change greatly, mainly because the vdo device excludes zero blocks.
If your host has large non empty files, you can do this test again to detect the following vdo deduplication functions. It should be noted that to detect duplicate data, it is necessary to ensure that there are at least two files with the same content in vdo, and observe the storage occupancy before and after duplicate files.
5. Permanent mounting of VDO
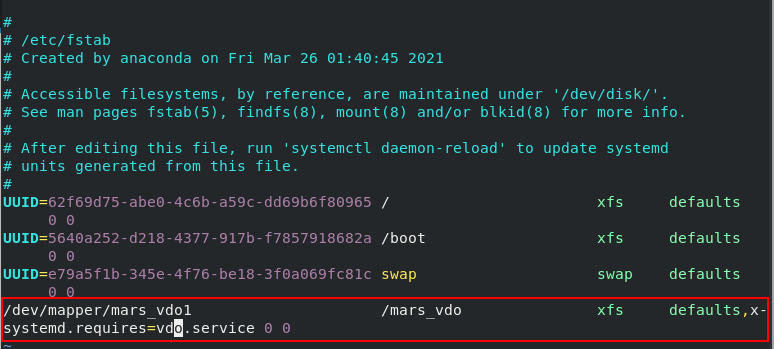
When it comes to permanent mount, we must first think of our device mount policy file / etc/fstab. If we want permanent mount, that is, our vdo devices can be automatically mounted to the specified directory when the system is powered on, we need to write the files we just mentioned. The contents of the files are as follows:
/dev/mapper/mars_vdo /mars_vdo xfs defaults,x-systemd.requires=vdo.service 0 0
Note: x-systemd.requires=vdo.service means that the vdo service needs to be started before the directory is mounted. It must be available. Otherwise, the vdo service may fail to mount and cannot be started when the directory is started.
The relevant commands are as follows:
vim /etc/fstab Write device mount policy document/etc/fstab reboot Restart the system df -h View mounted devices
The specific operations are as follows:

 The device mounting policy file is as follows:
The device mounting policy file is as follows:
After restarting the device, df queries the mounted device and finds that the vdo device has been automatically mounted.
6. Delete VDO
Finally, let's take a look at the last part of VDO. How does VDO deletion operate?
The command to delete VDO device flow is as follows:
umount /mars_vdo Uninstall before deleting the device vim /etc/fstab Delete auto mount VDO Content of vdo stop --name mars_vdo1 close VDO equipment vdo remove --name mars_vdo1 delete VDO equipment ls -l /dev/mapper Check whether the deletion is successful
The specific operations are as follows:
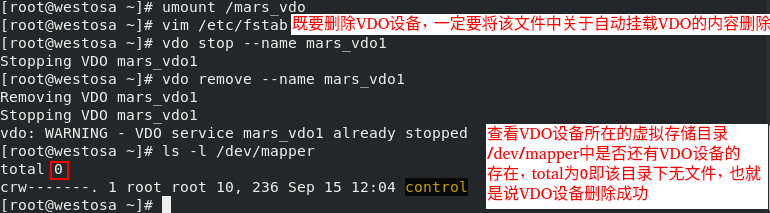
That's all about VDO~~~~~~~
See you in the next article