preface
The first week mainly describes the basic grammar of C language, and the content is relatively simple; However, there are several challenging homework questions. This paper mainly records the class content and challenging homework of this week for self summary after class.
1, 2021 / 12 / 28 - Day1
Day1 describes various preparations before writing code, such as environment installation.
2, 2021 / 12 / 29 - Day2
Day2 describes data types, binary conversion and standard input.
1. Find the common elements in n ascending arrays
Analysis: just find the common elements of the two arrays and save them in the array result; Then find the common elements of result array and other arrays; Until the result is empty or compared with other arrays. The problem can be decomposed into the problem of finding the common elements of two ascending arrays.
Find out the common elements of two ascending arrays a and B: point to the first element of a and B with two pointers pointA and pointB respectively. If a[pointA] < B [pointB], pointA+1; If a[pointA] = b[pointB], store a[pointA] in the result array; If a[pointA] > b [pointB], pointB+1. Until the array a or B is traversed, the result array stores the common elements of a and B.
Find the common element codes of two ascending arrays a and B as follows:
//count is the length of the result array
int count = 0;
//The return value is an array of common elements
int* FindPublic(int a[], int b[], int NumA, int NumB) {
int pointA = 0, pointB = 0;
int* result = (int*)malloc(sizeof(int) * NumA);
count = 0;
while (pointA < NumA && pointB < NumB) {
if (a[pointA] < b[pointB])
pointA++;
else if (a[pointA] > b[pointB])
pointB++;
else {
result[count] = a[pointA];
pointA++;
pointB++;
count++;
}
}
return result;
}
Find the common element code of n ascending arrays as follows:
result = FindPublic(a , b , numA , numB);
for(int i = 0; i < n - 2;i++){
numA = count;
if(numA == 0){
break;
}
printf("Please Input the arrLen:");
scanf("%d", &numB);
printf("Please Input the %dth array:", i);
for(int j = 0; j < numB; j++){
scanf("%d", &b[j]);
}
result = FindPublic(result, b, count, numB);
}
2. Given an array a of n integer elements, where one element occurs more than n/2, find this element
analysis:
Idea 1: sort first and then find. But the sorting efficiency is very low;
Idea 2: save the occurrence times of different elements through hash table. You only need to traverse array a once and the hash table once. Time complexity O(n); The space complexity is related to the number of different elements in array a;
Idea 3: make use of the idea of selecting people during the election; If there is a candidate with more than n/2 votes, the candidate has more votes than the sum of the votes of other candidates.
Candidate stores the currently dominant candidate, and priority represents the advantage of the current candidate; Set the initial value of candidate to a[0], and the initial value of prior to 0; Traverse the entire array from a[0].
The conditions for the end of traversal are: (1) traversal of a complete array or (2) the value of prior is greater than n/2.
If the current array element a [k]= Candidate, the advantage of the original candidate becomes smaller, priority-1; Otherwise, priority + 1. When priority = - 1, it indicates that the current candidate has lost the vote advantage, update candidate candidate=a[k], and set priority = 1.
This method only needs to traverse one side array a, and only needs constant level additional space. The time complexity is O(n) and the space complexity is O(1).
The code is as follows:
void Find_candidate() {
int* A, NumA;
int candidate, prior;
printf("Please Input the arrlen:");
scanf("%d", &NumA);
A = (int*)malloc(sizeof(int) * NumA);
printf("Please Input the arry elem:");
for (int i = 0; i < NumA; i++)
scanf("%d", &A[i]);
int i = 0;
prior = 0;
candidate = A[0];
while (i < NumA && prior <= NumA / 2) {
if (A[i] == candidate) {
prior++;
}
else {
prior--;
if (prior == -1) {
candidate = A[i];
prior = 1;
}
}
i++;
}
if (prior >= 1) {
printf("The Element is %d\n", candidate);
}
else {
printf("No such Element\n");
}
}
3, 2021 / 12 / 30 - Day3
Day3 describes various input and output functions (scanf, getchar, printf, putchar); Describe the operation mode and priority of various operators; Describes the syntax for selecting loops.
1. Input characters from the keyboard and count the number of letters, numbers and other characters; Print the number of letters, numbers and other characters in the form of histogram.
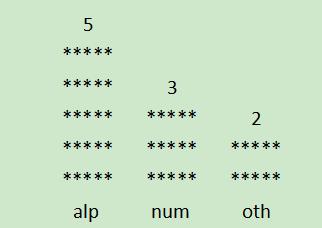
This question is not for the time being. It only counts the number of various characters. How to print has not been mentioned. Waiting for update~
2. There are 101 integers, of which 50 numbers appear twice and 1 number appears once. Find the number that appears once.
Analysis: use XOR operation: the XOR result of two identical numbers is 0; The result of the exclusive or of any number a and 0 is itself. XOR the numbers in the array in turn, and the result is the number that appears only once.
The code is as follows:
void AppearOnce() {
int a[101];
int num = 0;
printf("Please Enter 101 Numbers:");
for (int i = 0; i < 101; i++) {
scanf("%d", &a[i]);
num = num ^ a[i];
}
printf("Number %d is the Only Appear Once\n", num);
}
3. There are 102 integers, of which 50 numbers appear twice and 2 numbers appear once. Find out the two numbers that appear once.
Analysis: divide 102 numbers into two piles, and divide two numbers a and b that only appear once into two piles.
What kind of two piles are divided into: divide x and y into two different heapA and heapB, and make the same number in the same pile. The problem can be divided into two problems 2 1.
How to stack:
- XOR array a in turn to get the number M. The number m is essentially obtained from the XOR of x and y, and m= 0
- According to the law of XOR, the corresponding values of X and y are different for the bit of "1" in the binary representation of m. For example, x = (1001 0010)B, y = (1010 1010)B, m = x ^ y = (0011 1000)B. in binary, the 4th, 5th and 6th bits of m are 1, that is, it is proved that the 4th, 5th and 6th bits of X and y are different from each other;
- Therefore, you only need to find the lowest bit "1" of m and sort it according to the value of each number in array a. It can be realized: (1) divide all the same numbers into the same pile; (2) Divide x and y into different piles
The code is as follows:
void AppearOnce() {
int a[102];
int num = 0;
printf("Please Enter 102 Numbers:");
for (int i = 0; i < 102; i++) {
scanf("%d", &a[i]);
num = num ^ a[i];
}
//Find the lowest 1 in num
int cmp = 1;
while ( !(cmp & num)) {
cmp = cmp << 1;
}
int num1 = 0, num2 = 0;
for (int i = 0; i < 102; i++) {
if (a[i] & cmp) {
num1 = num1 ^ a[i];
}
else {
num2 = num2 ^ a[i];
}
}
printf("Number %d and %d are the Only Appear Once\n", num1, num2);
}
4. There are 103 integers, of which 50 numbers appear twice and three numbers appear once. Find out the three numbers that appear once.
Analysis: divide 103 numbers into two piles
What kind of two piles are divided into: divide x, y and z into two different heapA and heapB, and make the same number in the same pile. Where there are two numbers in X, y and z in one heap and one number in X, y and z in the other heap. The problem can be decomposed into a problem 2 1 , one question 3 2.
How to stack (violent stacking, up to 32 times):
- Starting from count = 1, the number with a & count result of true in array A is divided into heapA and the number with a & count result of false is divided into heapB. Then move the count one bit to the left.
- Since the odd number is divided into two piles, there must be an even number in one pile and an odd number in the other. Next, you need to judge whether to divide X and Y into this heap in the even heap. The judgment method is: XOR all the numbers in the even heap in turn. If the result is 0, it means that x, y and z are in the odd heap. It is necessary to move the count to the left and divide the heap again.
The code is as follows (only the code of heap splitting is included):
void Divide_Heap() {
int a[103], Heapa[103], Heapb[103];
int HeapaLen = 0;
int HeapbLen = 0;
printf("Please Enter 103 Numbers:");
for (int i = 0; i < 103; i++) {
scanf("%d", &a[i]);
}
int count = 1;
//divide
for (int i = 0; i < 32; i++) {
for (int j = 0; j < 103; j++) {
if (a[j] & count) {
Heapa[HeapaLen] = a[j];
HeapaLen++;
}
else {
Heapb[HeapbLen] = a[j];
HeapbLen++;
}
}
int numa = 0;
int numb = 0;
for (int j = 0; j < HeapaLen - 1; j++) {
numa = numa ^ Heapa[j];
}
for (int j = 0; j < HeapbLen - 1; j++) {
numb = numb ^ Heapb[j];
}
if (numa != 0 && numb != 0) {
break;
}
i++;
count = count << 1;
}
}
4, December 31, 2021 - Day4
Day4 describes the properties of one-dimensional array, two-dimensional array and character array. The new year's Eve question is relatively simple and very gingko oriented.
5, 2022 / 1 / 1 - Day5
Day5 tells about the pointer, the transmission and nature of the pointer; Formal and arguments in functions.
1. Large integer addition. Realize the addition of two integers in any range (the range of integers cannot be represented by int variables, 50 bits)
Analysis: use the string to store the large integers a and b, then add them from low to high, and store them in the empty string c (note that the content stored in C is opposite to the result, and C should be turned over to get the correct answer)
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
//Flip a[left] to a[right] content
void Flip(char a[], int left, int right) {
char c;
while (left < right) {
c = a[left];
a[left] = a[right];
a[right] = c;
left++;
right--;
}
}
int main() {
while (1) {
char a[51], b[51],sum[52];
printf("Please enter a large integer a((no more than 50 digits):");
gets(a);
printf("Please enter a large integer b((no more than 50 digits):");
gets(b);
int lenA = strlen(a);
int lenB = strlen(b);
int i = lenA - 1;
int j = lenB - 1;
int add = 0;
int numA, numB;
//c=0 means no low carry, and c=1 means there is low carry
int c = 0;
while (i >= 0 && j >= 0) {
numA = a[i] - '0';
numB = b[j] - '0';
int k = numA + numB + c;
if (k >= 10) {
c = 1;
sum[add] = k - 10 + '0';
}
else {
sum[add] = k + '0';
c = 0;
}
i--;
j--;
add++;
}
while (i >= 0) {
numA = a[i] - '0';
int k = numA + c;
if (k >= 10) {
c = 1;
sum[add] = k - 10 + '0';
}
else {
c = 0;
sum[add] = k + '0';
}
i--;
add++;
}
while (j >= 0) {
numB = b[j] - '0';
int k = numB + c;
if (k >= 10) {
c = 1;
sum[add] = k - 10 + '0';
}
else {
c = 0;
sum[add] = k + '0';
}
j--;
add++;
}
sum[add] = 0;
Flip(sum, 0, add - 1);
printf("a+b=");
puts(sum);
}
return 0;
}
Thinking: can we refer to the CLA four bit adder in the composition principle to generate four bit carry at one time instead of one bit from low to high?