/*  

*Copyright (c)2017, School of computer and control engineering, Yantai University

*All rights reservrd.           

*Author: Li Xinhao

*Completion time: November 26, 2017

*Version number: v1.0

*Problem Description: topological sorting algorithm verification

The following figure is an example:

1, Based on graph.h, the header file of graph database

Add the function void TopSort(ALGraph *G); declare

The code is as follows:

#ifndef GRAPH_H_INCLUDED
#define GRAPH_H_INCLUDED

#define MAXV 100 / / maximum number of vertices
#Define inf 32767 / / inf means ∞
typedef int InfoType;

//The following defines the type of adjacency matrix
typedef struct
{
    int no;                     //Vertex number
    InfoType info;              //Other information of vertex, where the weight of weighted graph is stored
} VertexType;                   //Vertex Type

typedef struct                  //Definition of Graphs
{
    int edges[MAXV][MAXV];      //adjacency matrix
    int n,e;                    //Number of vertices, arcs
    VertexType vexs[MAXV];      //Store vertex information
} MGraph;                       //Adjacency matrix types of Graphs

//The following defines the adjacency table type
typedef struct ANode            //Node structure type of arc
{
    int adjvex;                 //End position of the arc
    struct ANode *nextarc;      //Pointer to the next arc
    InfoType info;              //The relevant information of the arc is used to store the weight
} ArcNode;

typedef int Vertex;

typedef struct Vnode            //Types of adjacent header nodes
{
    Vertex data;                //Vertex information
    int count;                  //Store vertex access, only used in topological sorting
    ArcNode *firstarc;          //Point to the first arc
} VNode;

typedef VNode AdjList[MAXV];    //AdjList is an adjacency table type

typedef struct
{
    AdjList adjlist;            //Adjacency list
    int n,e;                    //Vertex number n and edge number e in the graph
} ALGraph;                      //Adjacency table types of Graphs

//Function: construct a graph stored by adjacency matrix from a 2D array reflecting the adjacency relationship of vertices in the graph
//Parameter: Arr - array name. Since the formal parameter is a two-dimensional array, the number of elements in each row must be given. Here, the parameter Arr is declared as a one-dimensional array name (pointer to int)
//      The order of n - matrix
//      g - adjacency matrix data structure to be constructed
void ArrayToMat(int *Arr, int n, MGraph &g); //Constructing adjacency matrix of graph with common array
void ArrayToList(int *Arr, int n, ALGraph *&); //Constructing adjacency table of graph with common array
void MatToList(MGraph g,ALGraph *&G);//Transforming adjacency matrix G into adjacency table G
void ListToMat(ALGraph *G,MGraph &g);//Transforming adjacency table g into adjacency matrix G
void DispMat(MGraph g);//Output adjacency matrix g
void DispAdj(ALGraph *G);//Output adjacency table G





void TopSort(ALGraph *G);

#endif // GRAPH_H_INCLUDED

2, Define these functions in the source file graph.cpp file:

#include <stdio.h>
#include <malloc.h>
#include "graph.h"

//Function: construct a graph stored by adjacency matrix from a 2D array reflecting the adjacency relationship of vertices in the graph
//Parameter: Arr - array name. Since the formal parameter is a two-dimensional array, the number of elements in each row must be given. Here, the parameter Arr is declared as a one-dimensional array name (pointer to int)
//      The order of n - matrix
//      g - adjacency matrix data structure to be constructed
void ArrayToMat(int *Arr, int n, MGraph &g)
{
    int i,j,count=0;  //Count is used to count the number of sides, that is, the number of non-zero elements in the matrix
    g.n=n;
    for (i=0; i<g.n; i++)
        for (j=0; j<g.n; j++)
        {
            g.edges[i][j]=Arr[i*n+j]; //The Arr is regarded as a two-dimensional array of n × n, and the Arr[i*n+j] is the Arr[i][j]
            if(g.edges[i][j]!=0 && g.edges[i][j]!=INF)
                count++;
        }
    g.e=count;
}

void ArrayToList(int *Arr, int n, ALGraph *&G)
{
    int i,j,count=0;  //Count is used to count the number of sides, that is, the number of non-zero elements in the matrix
    ArcNode *p;
    G=(ALGraph *)malloc(sizeof(ALGraph));
    G->n=n;
    for (i=0; i<n; i++)                 //Set the initial value of the pointer field of all header nodes in the adjacency table
        G->adjlist[i].firstarc=NULL;
    for (i=0; i<n; i++)                 //Check every element in adjacency matrix
        for (j=n-1; j>=0; j--)
            if (Arr[i*n+j]!=0)      //There is an edge. Consider Arr as a two-dimensional array of n × n. Arr[i*n+j] is Arr[i][j]
            {
                p=(ArcNode *)malloc(sizeof(ArcNode));   //Create a node * p
                p->adjvex=j;
                p->info=Arr[i*n+j];
                p->nextarc=G->adjlist[i].firstarc;      //Insert * p by head insertion
                G->adjlist[i].firstarc=p;
            }

    G->e=count;
}

void MatToList(MGraph g, ALGraph *&G)
//Transforming adjacency matrix G into adjacency table G
{
    int i,j;
    ArcNode *p;
    G=(ALGraph *)malloc(sizeof(ALGraph));
    for (i=0; i<g.n; i++)                   //Set the initial value of the pointer field of all header nodes in the adjacency table
        G->adjlist[i].firstarc=NULL;
    for (i=0; i<g.n; i++)                   //Check every element in adjacency matrix
        for (j=g.n-1; j>=0; j--)
            if (g.edges[i][j]!=0)       //There is an edge
            {
                p=(ArcNode *)malloc(sizeof(ArcNode));   //Create a node * p
                p->adjvex=j;
                p->info=g.edges[i][j];
                p->nextarc=G->adjlist[i].firstarc;      //Insert * p by head insertion
                G->adjlist[i].firstarc=p;
            }
    G->n=g.n;
    G->e=g.e;
}

void ListToMat(ALGraph *G,MGraph &g)
//Transforming adjacency table g into adjacency matrix G
{
    int i,j;
    ArcNode *p;
    g.n=G->n;   //According to the first floor students "report" change. g.n is not assigned, the following initialization does not work
    g.e=G->e;
    for (i=0; i<g.n; i++)   //Initialize adjacency matrix first
        for (j=0; j<g.n; j++)
            g.edges[i][j]=0;
    for (i=0; i<G->n; i++)  //Assign values to adjacency matrix according to adjacency table
    {
        p=G->adjlist[i].firstarc;
        while (p!=NULL)
        {
            g.edges[i][p->adjvex]=p->info;
            p=p->nextarc;
        }
    }
}

void DispMat(MGraph g)
//Output adjacency matrix g
{
    int i,j;
    for (i=0; i<g.n; i++)
    {
        for (j=0; j<g.n; j++)
            if (g.edges[i][j]==INF)
                printf("%3s","∞");
            else
                printf("%3d",g.edges[i][j]);
        printf("\n");
    }
}

void DispAdj(ALGraph *G)
//Output adjacency table G
{
    int i;
    ArcNode *p;
    for (i=0; i<G->n; i++)
    {
        p=G->adjlist[i].firstarc;
        printf("%3d: ",i);
        while (p!=NULL)
        {
            printf("-->%d/%d ",p->adjvex,p->info);
            p=p->nextarc;
        }
        printf("\n");
    }
}





void TopSort(ALGraph *G)
{
    int i,j;
    int St[MAXV],top=-1;            //The pointer of stack St is top
    ArcNode *p;
    for (i=0; i<G->n; i++)          //Entry setting initial value 0
        G->adjlist[i].count=0;
    for (i=0; i<G->n; i++)          //Find the degree of entry of all vertices
    {
        p=G->adjlist[i].firstarc;
        while (p!=NULL)
        {
            G->adjlist[p->adjvex].count++;
            p=p->nextarc;
        }
    }
    for (i=0; i<G->n; i++)
        if (G->adjlist[i].count==0)  //Enter the vertex stack of 0
        {
            top++;
            St[top]=i;
        }
    while (top>-1)                  //Stack is not a space-time loop
    {
        i=St[top];
        top--;              //Stack out
        printf("%d ",i);            //Output vertex
        p=G->adjlist[i].firstarc;   //Find the first adjacent vertex
        while (p!=NULL)
        {
            j=p->adjvex;
            G->adjlist[j].count--;
            if (G->adjlist[j].count==0)//Stack adjacent vertices with degree 0
            {
                top++;
                St[top]=j;
            }
            p=p->nextarc;       //Find next adjacent vertex
        }
    }
}

3, Complete the test in the source file main.cpp

The code is as follows:

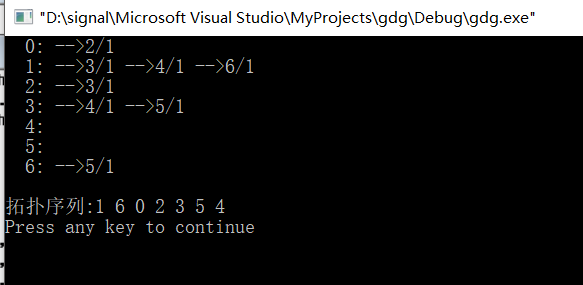
#include <stdio.h>
#include <malloc.h>
#include "graph.h"
int main()
{
    ALGraph *G;
    int A[7][7]=
    {
        {0,0,1,0,0,0,0},
        {0,0,0,1,1,0,1},
        {0,0,0,1,0,0,0},
        {0,0,0,0,1,1,0},
        {0,0,0,0,0,0,0},
        {0,0,0,0,0,0,0},
        {0,0,0,0,0,1,0}
    };
    ArrayToList(A[0], 7, G);
    DispAdj(G);
    printf("\n");
    printf("Topological sequence:");
    TopSort(G);
    printf("\n");
    return 0;
}

4, The screenshot of the test results is as follows: