5, Dichotomy, sort
source
Geek time 2021 algorithm training camp
Author: Li Yudong
1 dichotomy
1.1 basic idea
Binary search, also known as half search, is an efficient search method.
Binary search requirements
- The objective function is monotonic (monotonically increasing or decreasing)
- There is an upper and lower bound
- It can be accessed by index
1.2 direct finding method
Direct search method: if an element is found in the loop body, the result will be returned directly -- if the num [mid] value is greater than or less than the target value, take the interval [left, mid - 1] or [mid + 1, right] > > > > > > > > respectively, which is applicable to simple and non repetitive element search value problems
- python implementation
- with 704. Binary search As an example;
class Solution:
def search(self, nums: List[int], target: int) -> int:
left,right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
right = mid - 1
else:
left = mid + 1
return -1
Two details
- mid value problem
Common mid values are mid = (left + right) // 2 or mid = left + (right - left) // 2. The former is the most common way to write, and the latter is to prevent integer overflow. In the formula / / 2 means that the middle number is rounded down ------ left.
mid = (left + right + 1) // 2, or mid = left + (right - left + 1) // 2 can take the right, but generally speaking, taking the middle position element has the best effect in the average sense. At the same time, it's easiest to write like this. For the mid value to be rounded down or up, most of the time, you choose not to add 1 - Boundary condition problems ------------- left < = right and left < right
- Left < = right, and the searched element does not exist, the condition for the while judgment statement to be out of bounds is left == right + 1, which is written in the form of interval [right + 1, right]. At this time, the interval to be searched is empty, and there are no elements in the interval to be searched, so it is correct to terminate the loop and return -1 directly.
- If the judgment statement is left < right and the searched element does not exist, the out of bounds condition of the while judgment statement is left == right, which is written in interval form as [right, right]. At this time, the interval is not empty. There is another element in the interval to be found. It is not certain that the element to be found is not in this interval. At this time, it is wrong to terminate the loop return -1. > > > > Change to return left if num [left] = = target else - 1, and don't judge whether to return left or right
Namely:
class Solution:
def search(self, nums: List[int], target: int) -> int:
left,right = 0, len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
right = mid - 1
else:
left = mid + 1
return left if nums[left] == target else -1
1.3 lower_bound and upper_bound
- Find lower_bound (first > = number of targets)
The interval is divided into [mid + 1, right] and [left, mid]; And mid = left + (right - left) // 2:
class Solution:
def search(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1
# Find the target in the interval [left, right]
while left < right:
# Take the intermediate node of the interval
mid = left + (right - left) // 2
# Num s [mid] is less than the target value. Exclude the impossible interval [left, mid], and continue searching in [mid + 1, right]
if nums[mid] < target:
left = mid + 1
# nums[mid] is greater than or equal to the target value. The target element may be in [left, mid]. Continue searching in [left, mid]
else:
right = mid # nums[mid] >= target
# Judge whether the remaining elements in the interval are target elements. If not, return - 1
return right if nums[right] == target else -1
- Find upper_bound the number of the last < = target
The interval is divided into [left, mid - 1] and [mid, right]; And mid = left + (right - left + 1) // 2:
class Solution:
def search(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1
# Find the target in the interval [left, right]
while left < right:
# Take the intermediate node of the interval
mid = left + (right - left + 1) // 2
# Num s [mid] is greater than the target value. Exclude the impossible interval [mid, right], and continue searching in [left, mid - 1]
if nums[mid] > target:
right = mid - 1
# Num [mid] is less than or equal to the target value. The target element may be in [mid, right]. Continue searching in [mid, right]
else: # nums[mid] <= target
left = mid
# Judge whether the remaining elements in the interval are target elements. If not, return - 1
return right if nums[right] == target else -1
- When the distinction is divided into two parts: [left, mid - 1] and [mid, right], the mid value should be rounded up. That is, mid = left + (right - left + 1) // 2. Because if there are only two elements left in the interval (right = left + 1 at this time), once the left = mid branch is entered, the interval will not be narrowed. The search interval of the next cycle is still [left, right], and it will fall into an endless cycle.
1.4 related topics
1 153 . Find the smallest value in the rotation sort array
- Idea: after rotation, the array is divided into two sections and set to 0 and 1 in order, > > > which is equivalent to finding the lower_bound
class Solution:
def findMin(self, nums: List[int]) -> int:
left, right = 0, len(nums) - 1
while left < right:
mid = left + (right - left)//2
if nums[mid] < nums[right]:
right = mid
else:
left = mid + 1
return nums[right]
- Idea: the start position is the first greater than target, and the end position is the last < = target
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
ans = []
left, right = 0, len(nums)
while left < right:
mid = (left + right) // 2
if nums[mid] >= target:
right = mid
else:
left = mid + 1
ans.append(right)
left, right = -1, len(nums) - 1
while left < right:
mid = (left + right + 1) // 2
if nums[mid] <= target:
left = mid
else:
right = mid - 1
ans.append(right)
if ans[0] > ans[1]:
return [-1, -1]
else:
return ans
- upper_bound type
class Solution:
def mySqrt(self, x: int) -> int:
left, right = 0, x
while left < right:
mid = (left + right + 1) // 2
if mid * mid <= x:
left = mid
else:
right = mid - 1
return right
-
The trisection method is used to find the maximum value of single peak function (or the minimum value of single valley function)
The trisection method can also be used to find the local maximum / minimum of the function
Requirement: the function is piecewise strictly monotonically increasing / decreasing (a period of leveling is not allowed) -
Taking the maximum value of unimodal function f as an example, any two points IMID and rmid can be taken on the definition domain [L, r]
• if f (lmid) < = f (rmid), the function must monotonically increase at Imid, and the extreme value is on [Imid, r]
• if f (lmid) > F (rmid), the function must monotonically decrease at rmid, and the extreme value is on [L rmid] -
IMID and rmid can be taken as trisection points
Alternatively, Imid is the bisection point, and rmid is Lmid with a slight offset
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
left, right = 0, len(nums) - 1
while left < right:
lmid = (left + right) // 2
rmid = lmid + 1
if nums[lmid] < nums[rmid]:left = lmid + 1
else:right = rmid - 1
return right
- Idea: turn it into a decision problem > > > > give a value T, "is the maximum value of the respective sum of M sub arrays < = t" legal
class Solution:
def splitArray(self, nums: List[int], m: int) -> int:
def validate(nums, m, size):
box, count = 0, 1
for num in nums:
if num + box <= size:
box += num
else:
box = num
count += 1
return count <= m
left, right = 0, 0
for num in nums:
left = max(left, num)
right += num
while left <right:
mid = (right + left) // 2
if validate(nums, m, mid):
right = mid
else:
left = mid + 1
return right
class Solution:
def minDays(self, bloomDay: List[int], m: int, k: int) -> int:
def validate(bloomDay, m, k, now):
count, consecutive = 0, 0
for bloom in bloomDay:
if bloom <= now:
consecutive += 1
if consecutive == k:
consecutive = 0
count += 1
else:
consecutive = 0
return count >= m
latestbloom = 0
for bloom in bloomDay:
latestbloom = max(bloom, latestbloom)
left, right = 0, latestbloom + 1
while left < right:
mid = (left + right) // 2
if validate(bloomDay, m, k, mid):
right = mid
else:
left = mid + 1
return -1 if right == latestbloom + 1 else right
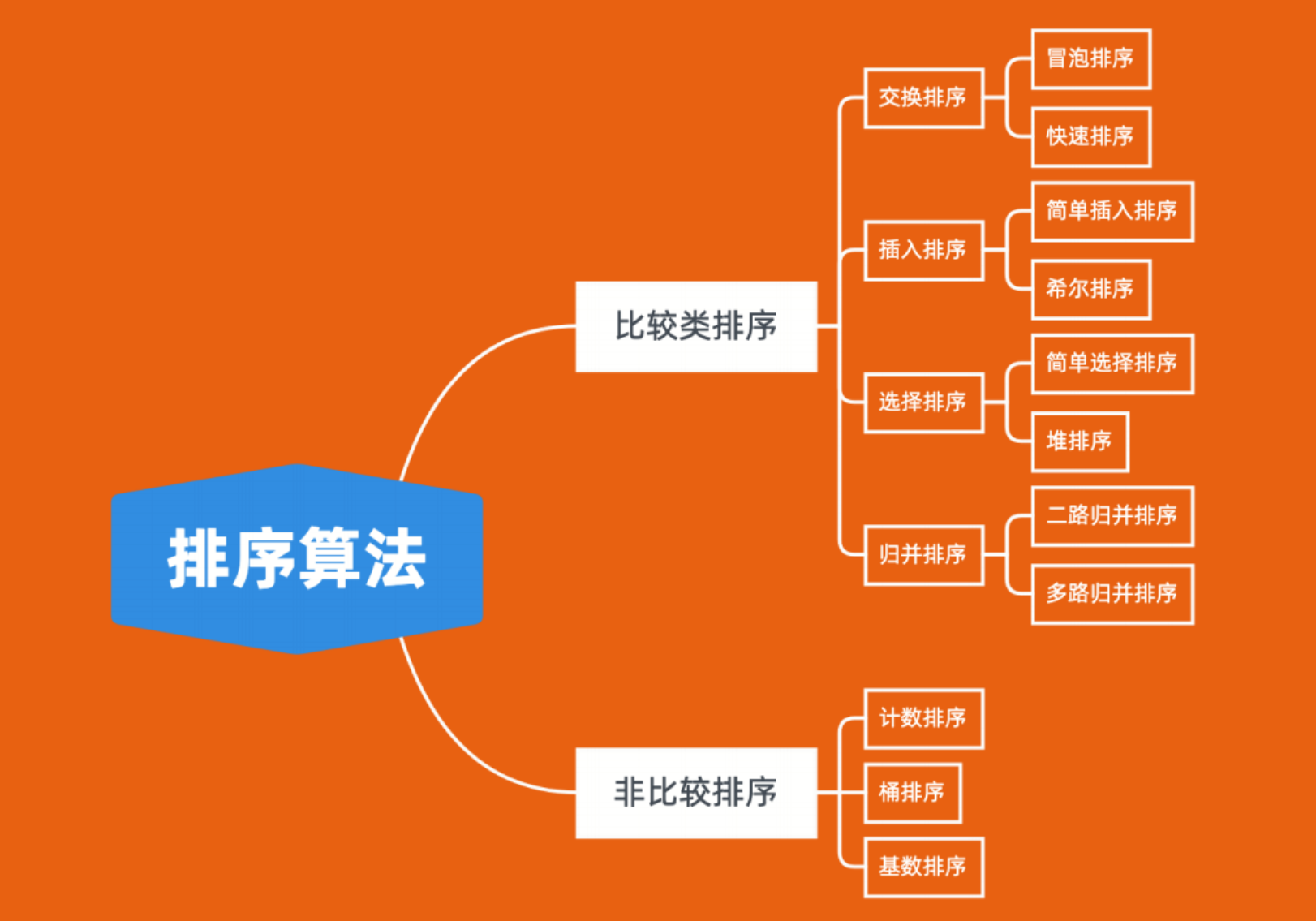
2 sorting
-
Comparison based sorting
The relative order between elements is determined by comparing the sizes
It can be proved that the lower bound of time complexity is O(logN) - it is impossible to break through this complexity to achieve faster speed -
Non comparison sort
The relative order between elements is not determined by comparing the sizes
The time complexity is affected by many factors such as the range and distribution of elements, and does not simply depend on the number of elements N
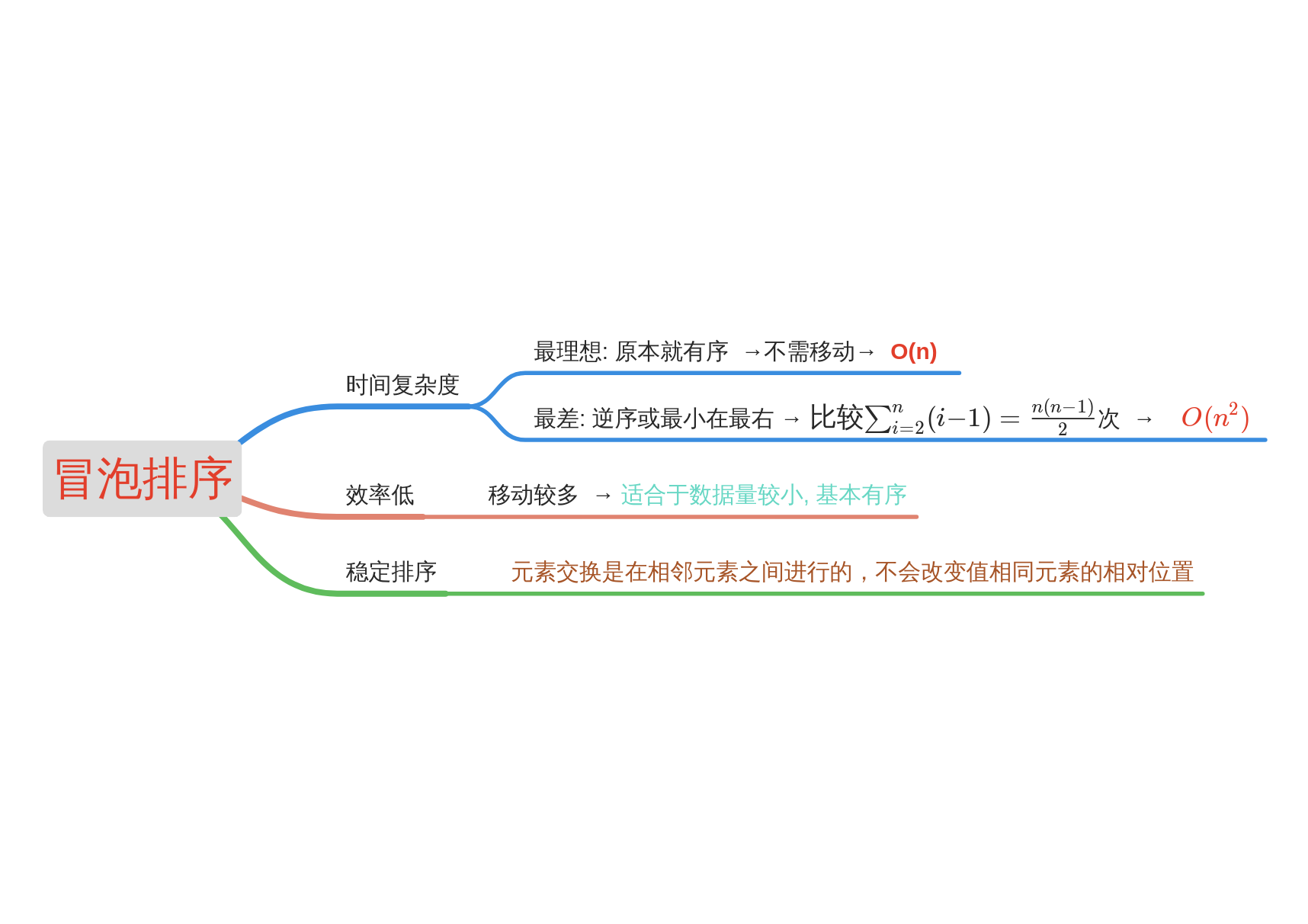
2.1 bubble sorting
Basic idea of Bubble Sort:
When sorting the i (i = 1, 2,...) pass, start from the first element of the first n - i + 1 element in the sequence, and compare the two adjacent elements. If the former is greater than the latter, the two exchange positions, otherwise they will not exchange.
- Algorithm steps:
-
Compare adjacent elements. If the first one is bigger than the second, exchange them.
-
Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end (n and n-1). After this step, the last element will be the maximum number.
-
Repeat the above steps for all elements except the last one.
-
Continue to repeat the above steps for fewer and fewer elements at a time until no pair of numbers need to be compared.
-
- Code implementation:
def bubbleSort(arr):
for i in range(len(arr)):
for j in range(len(arr) - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
- Algorithm analysis:
2.2 select sort
Basic idea of Selection Sort:
The i-th sorting selects an element with the smallest value from the last n − i + 1 (i = 1, 2,..., n − 1) elements of the sequence, and exchanges the position with the front element of the n - i + 1 element, that is, with the element at the i-th position of the whole sequence. This continues until i == n − 1 and the sorting ends.
step
-
First, find the smallest (large) element in the unordered sequence and store it at the beginning of the sorted sequence.
-
Then continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence.
-
Repeat step 2 until all elements are sorted.
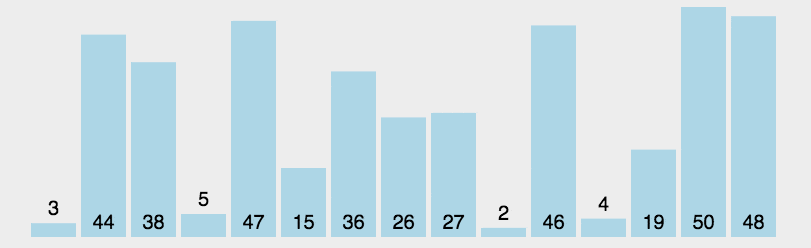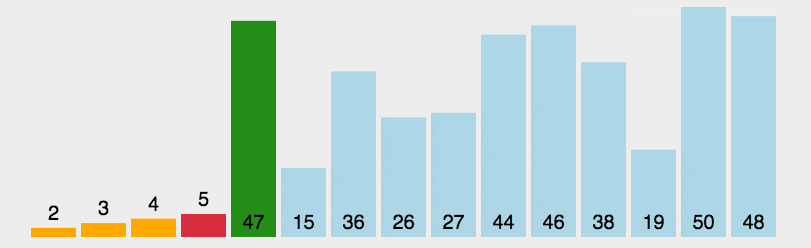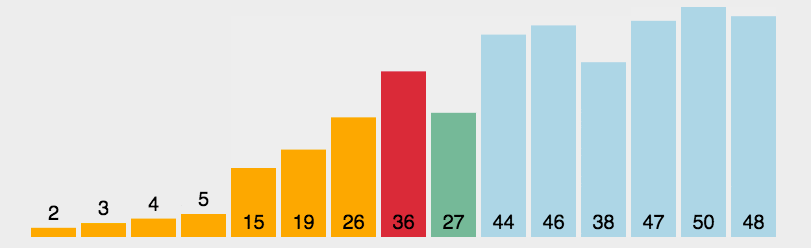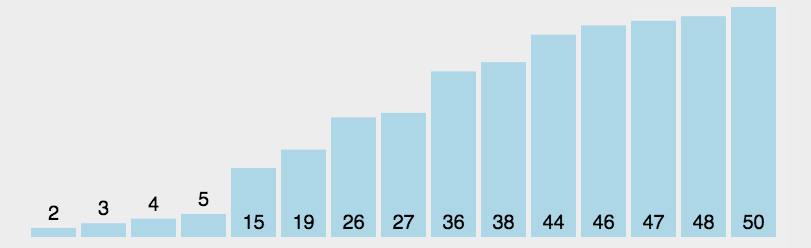python implementation:
def selectionSort(arr):
for i in range(len(arr) - 1):
# Records the index of the smallest decimal in an unordered sequence
min_i = i
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_i]:
min_i = j
# If the minimum number is found, the element at the i position is exchanged with the element at the minimum number
if i != min_i:
arr[i], arr[min_i] = arr[min_i], arr[i]
return arr
algorithm analysis
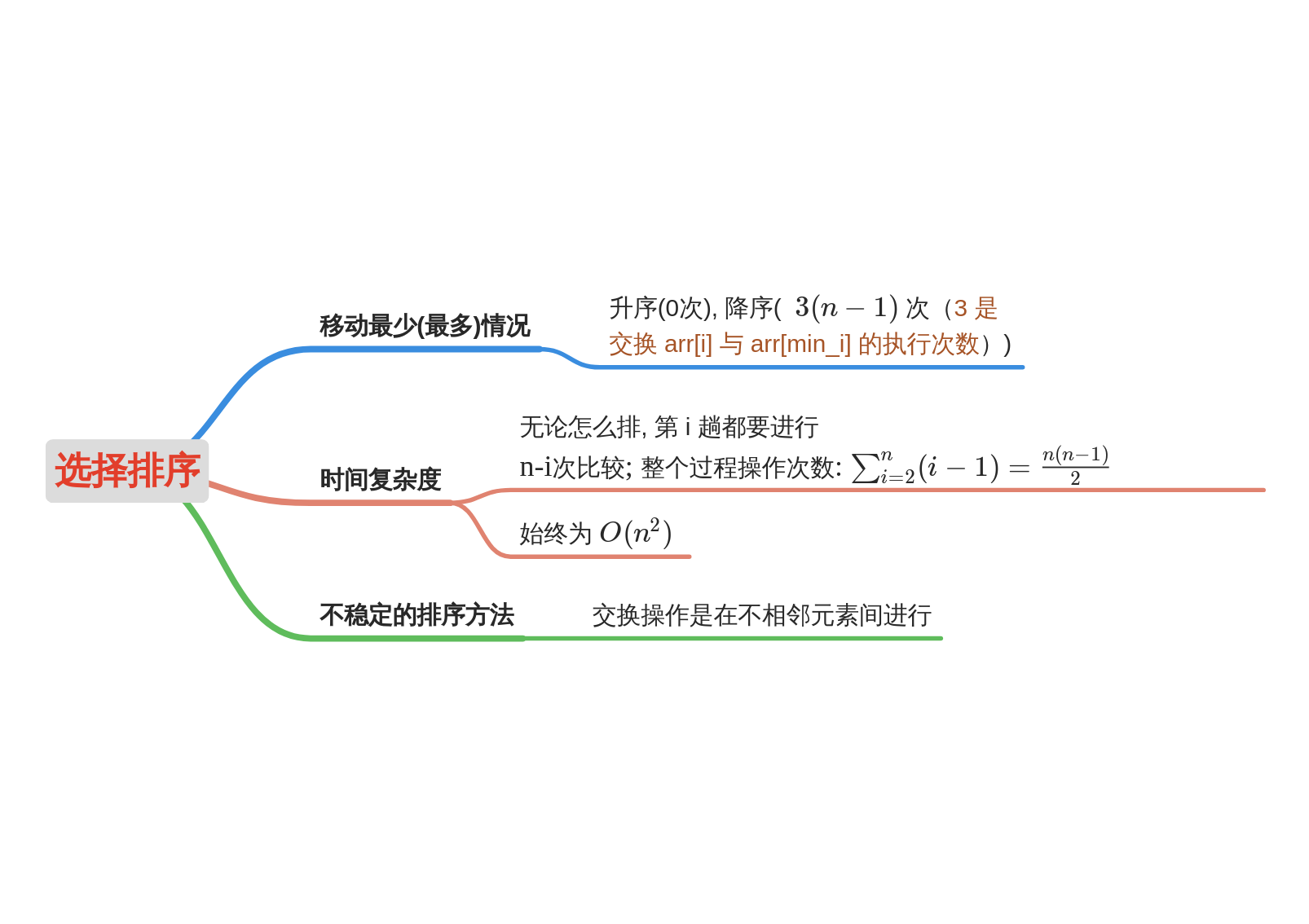
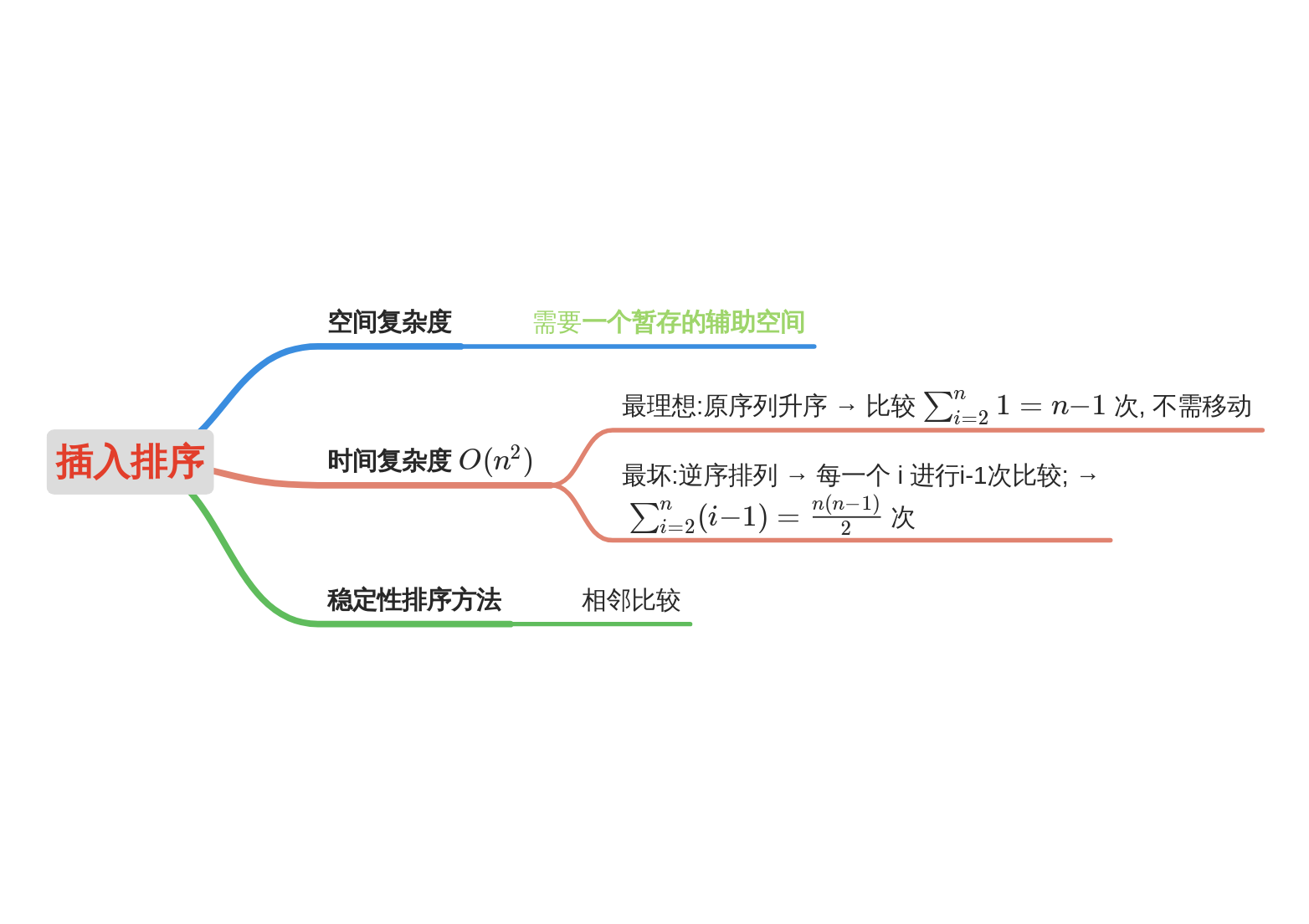
2.3 insert sort
Basic idea of Insertion Sort:
The whole sequence is divided into two parts: the first i - 1 element is an ordered sequence, and the last n - i + 1 element is an unordered sequence. In each sorting, the first element of the unordered sequence is found in the ordered sequence and inserted.
step
-
The first element of the first sequence to be sorted is regarded as an ordered sequence, and the second element to the last element is regarded as an unordered sequence.
-
Scan the unordered sequence from beginning to end, and insert each scanned element into the appropriate position of the ordered sequence. (if the element to be inserted is equal to an element in the ordered sequence, the element to be inserted is inserted after the equal element.)
python implementation
def insertionSort(a) for i in range(1, range(len(a)): # j start with 1 j = i temp = a[i] # Value corresponding to temporary storage i while j > 0 and a[j-1] > temp: #When the previous value is greater than the temporary value, change a[j], and j moves to the right a[j] = a[j-1] j -= 1 a[j] = temp # After the comparison, assign temp at the beginning of the compared element to insert return a
algorithm analysis
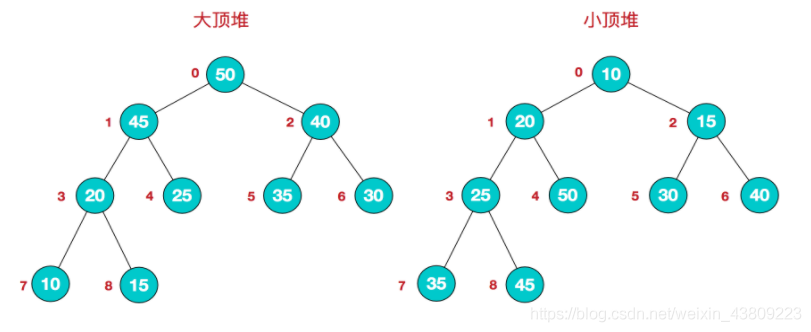
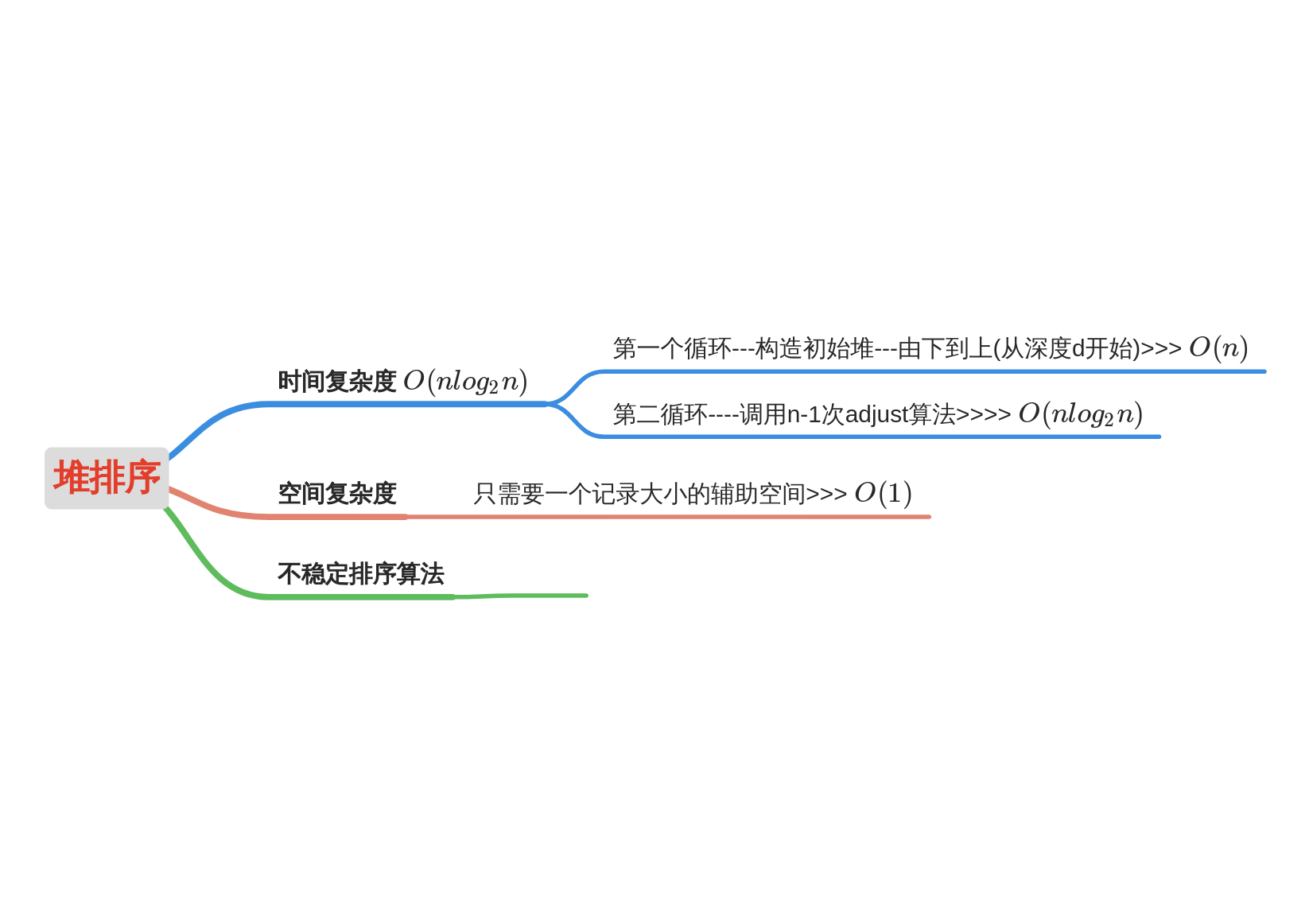
2.4 heap sorting
Heap sort is an optimization of selection sort
Basic idea of Heap sort:
Using the sorting algorithm designed by "heap structure". Convert the array into a large top heap, repeatedly take the node with the largest value from the large top heap, and let the remaining heap maintain the nature of a large top heap.
-
Heap: a complete binary tree that meets one of the following two conditions:
- Large top heap: root node value ≥ child node value.
- Small top heap: root node value ≤ child node value.
-
Steps:
-
a. Build the unnecessary sequence into a heap, and select the large top heap or small top heap according to the ascending and descending requirements;
-
b. Exchange the top element with the end element, and "sink" the largest element to the end of the array;
-
c. Readjust the structure to meet the heap definition, then continue to exchange the heap top elements with the current tail elements, and repeat the adjustment + exchange steps until the whole sequence is in order.
-
-
Source of specific steps: https://www.cnblogs.com/chengxiao/p/6129630.html
-
Step 1: construct the initial heap. The given disordered sequence is constructed into a large top heap (generally, the large top heap is used in ascending order and the small top heap is used in descending order).
(a). Assume that the given unordered sequence structure is as follows:
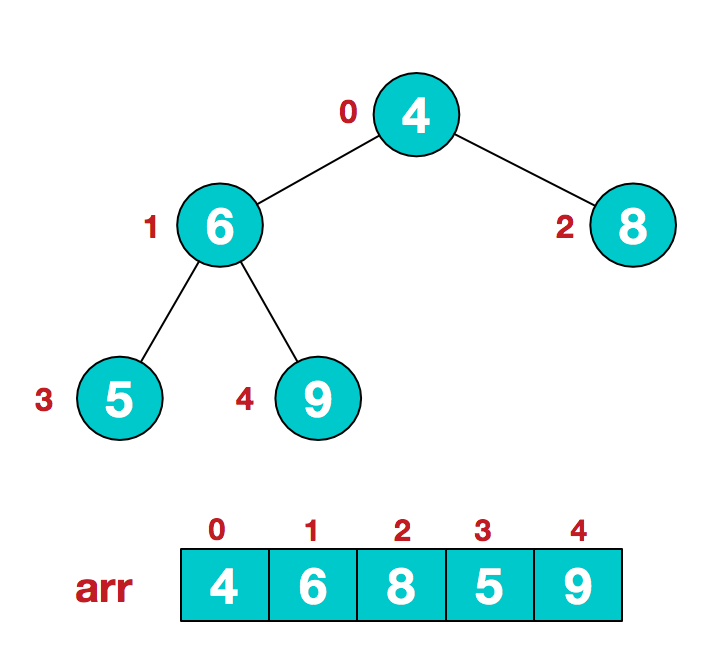
(b) At this time, we start from the last non leaf node (the leaf node does not need to be adjusted naturally. The first non leaf node arr.length/2-1=5/2-1=1, that is, the following 6 nodes), and adjust from left to right and from bottom to top.
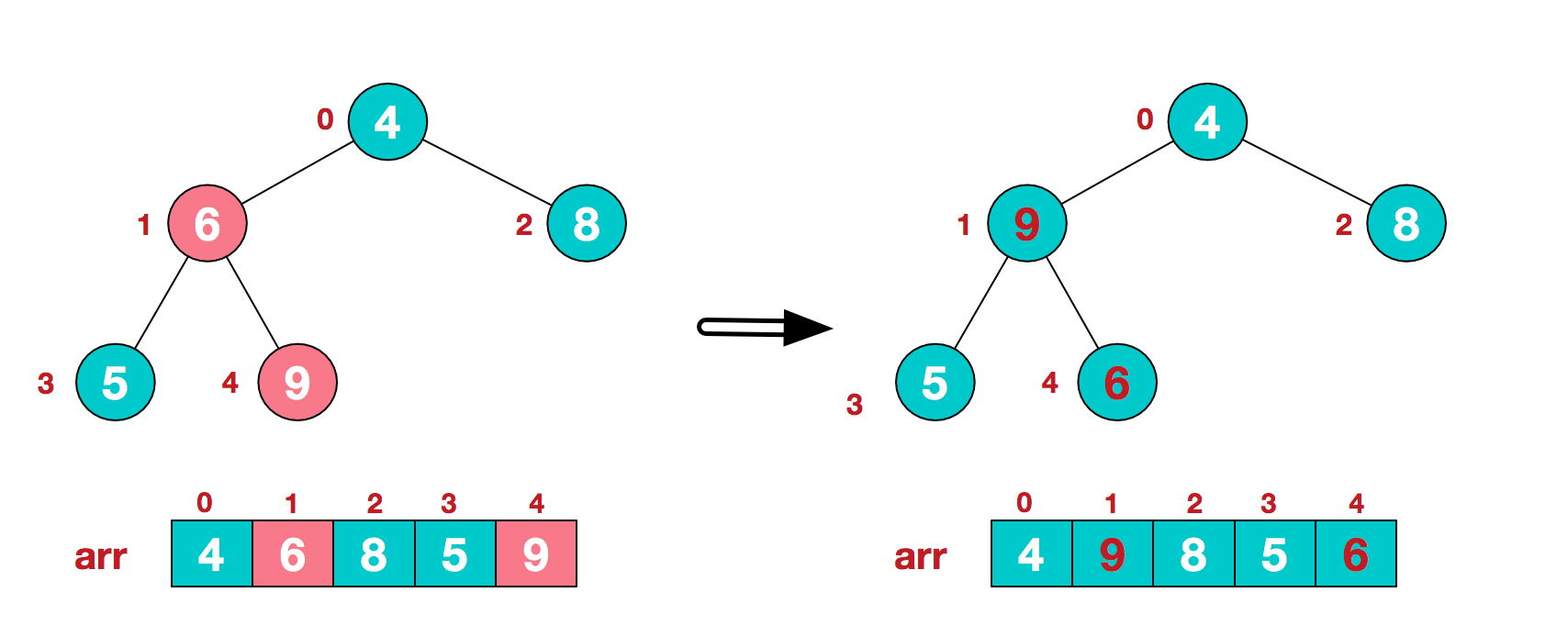
(c ). Find the second non leaf node 4. Since the 9 element in [4,9,8] is the largest, 4 and 9 exchange.
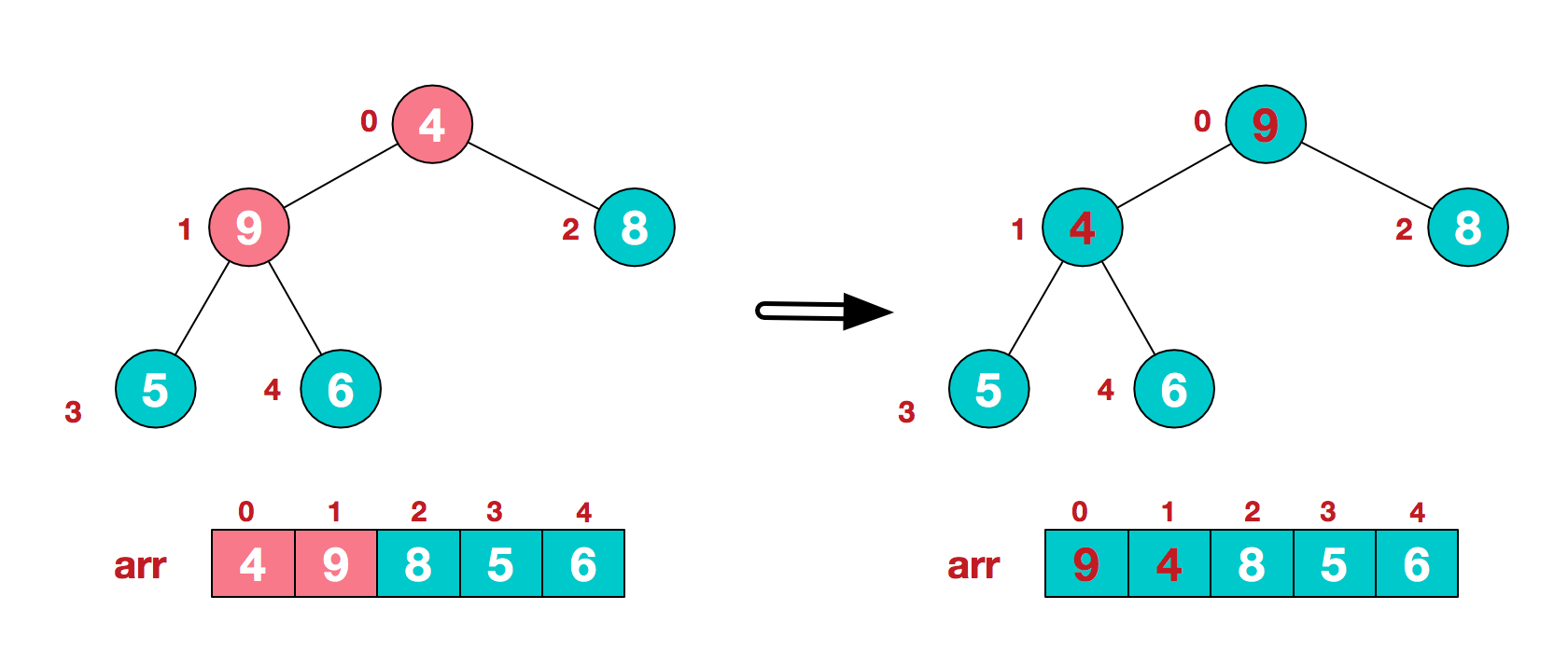
(d) The exchange leads to the confusion of the structure of the sub root [4,5,6]. Continue to adjust. 6 is the largest in [4,5,6], and exchange 4 and 6.
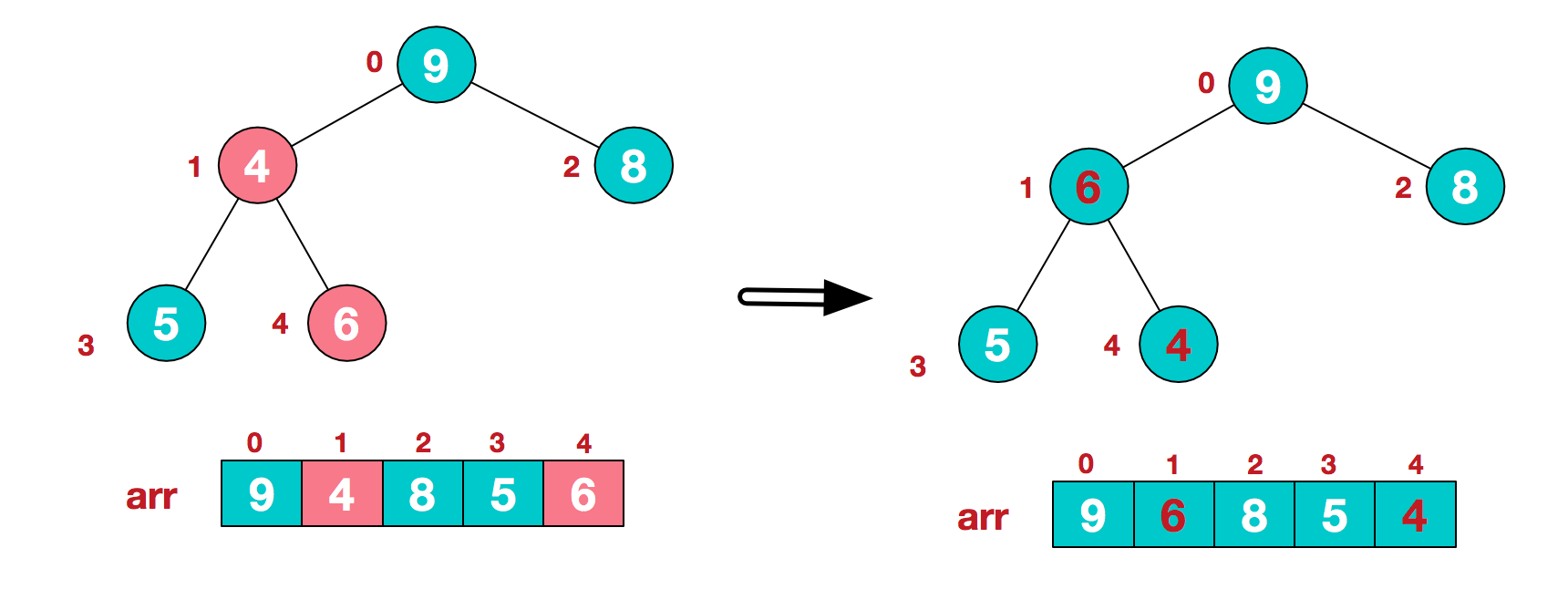
At this point, an unnecessary sequence is constructed into a large top heap.
-
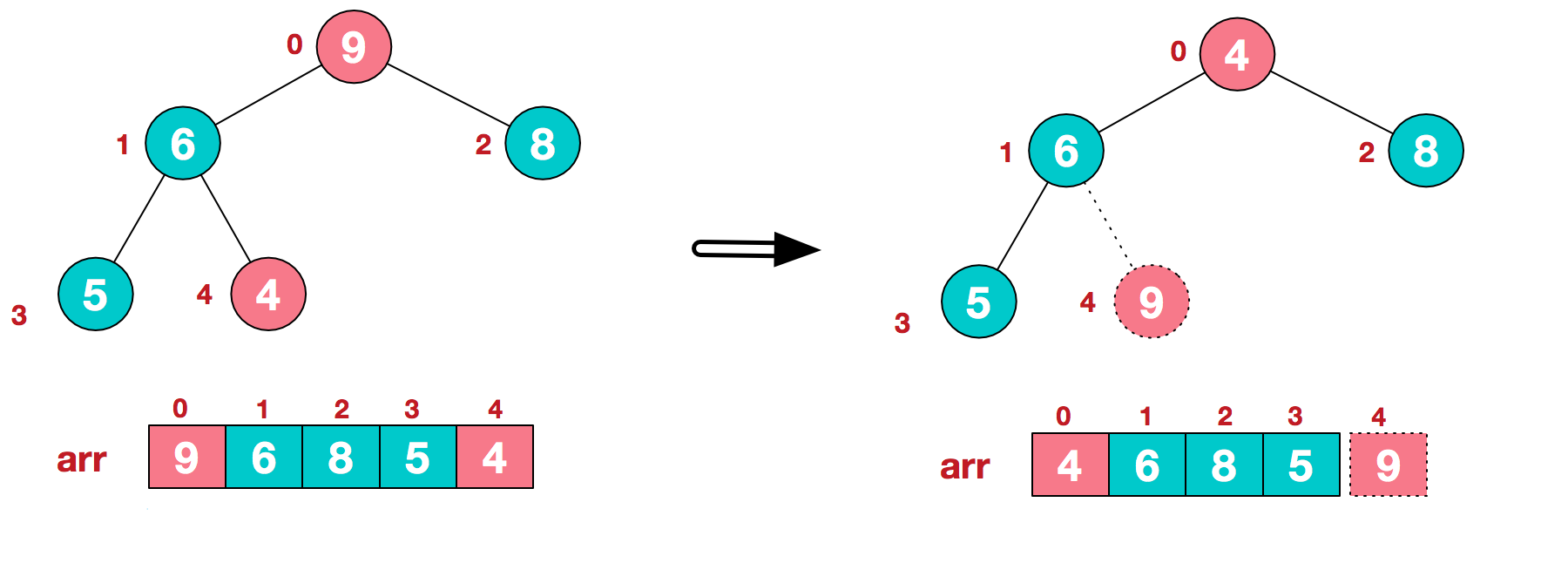
In step 2, the top element of the heap is exchanged with the last element to maximize the last element. Then continue to adjust the heap, and then exchange the top element with the end element to get the second largest element. Such repeated exchange, reconstruction and exchange.
(a) swap top element 9 and end element 4
(b) restructure to continue to meet the heap definition:
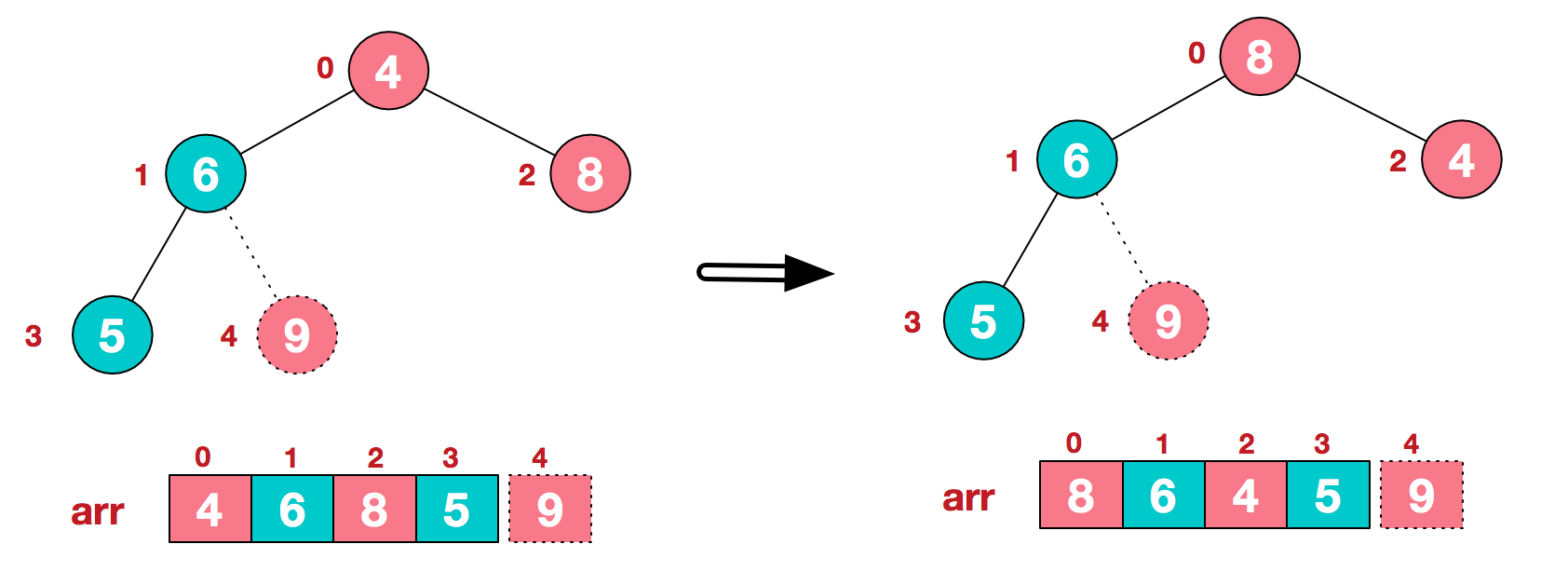
(c) exchange the top element 8 with the end element 5 to obtain the second largest element 8
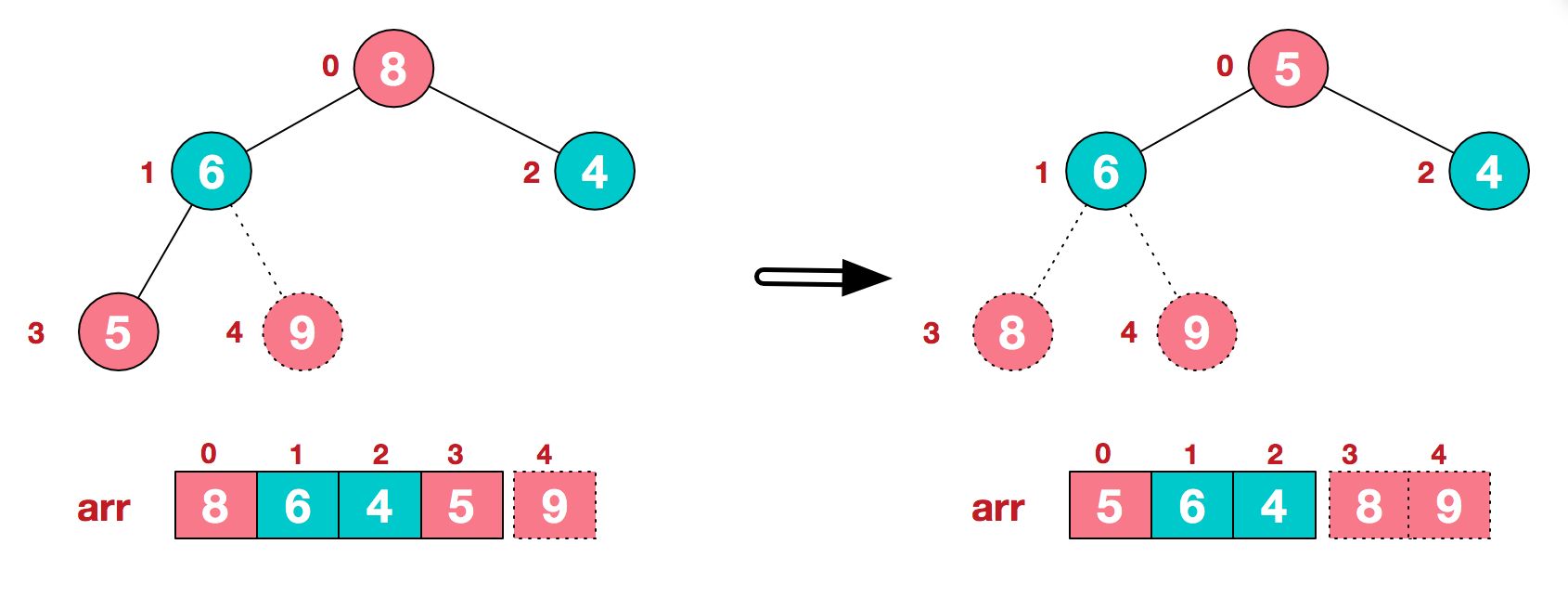
(d) in the subsequent process, continue to adjust and exchange, so as to make the whole sequence orderly:
-
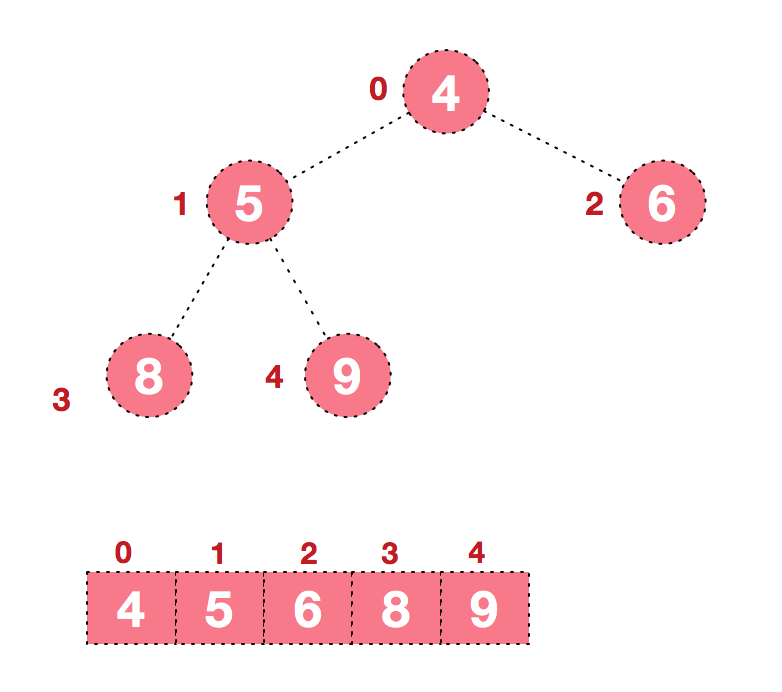
Dynamic diagram:
- code implementation
# Adjust full binary tree > > > > large top heap
def heapify(arr: [int], index: int, end: int ):
left = index * 2 + 1 #Left and right child nodes of index
right = left + 1
while left <= end: #When index is a non child node
max_index = index
if arr[left] > arr[max_index]:
max_index = left
if right <= end and arr[right] > arr[max_index]:
max_index = right
if index == max_index: #If the exchange is not needed, it indicates that the exchange has ended
break
arr[index],arr[max_index] = arr[max_index],arr[index]
index = max_index #Continue to adjust the next node
left = index * 2 + 1
right = left + 1
# Initialize large top heap
def buildMaxHeap(arr: [int]):
size = len(arr)
for i in range((size - 2)//2, - 1, - 1): # (size-2) / / 2 is the last non leaf node. Leaf nodes need not be adjusted
heapify(arr, i, size - 1)
return arr
def MaxHeapSort(arr: [int]):
buildMaxHeap(arr)
size = len(arr)
for i in range(size):
arr[0],arr[size - i - 1] = arr[size - i - 1],arr[0]
heapify(arr, 0, size - i - 2)
return arr
- algorithm analysis
2.5 Hill sort ----------- insert sort Pro
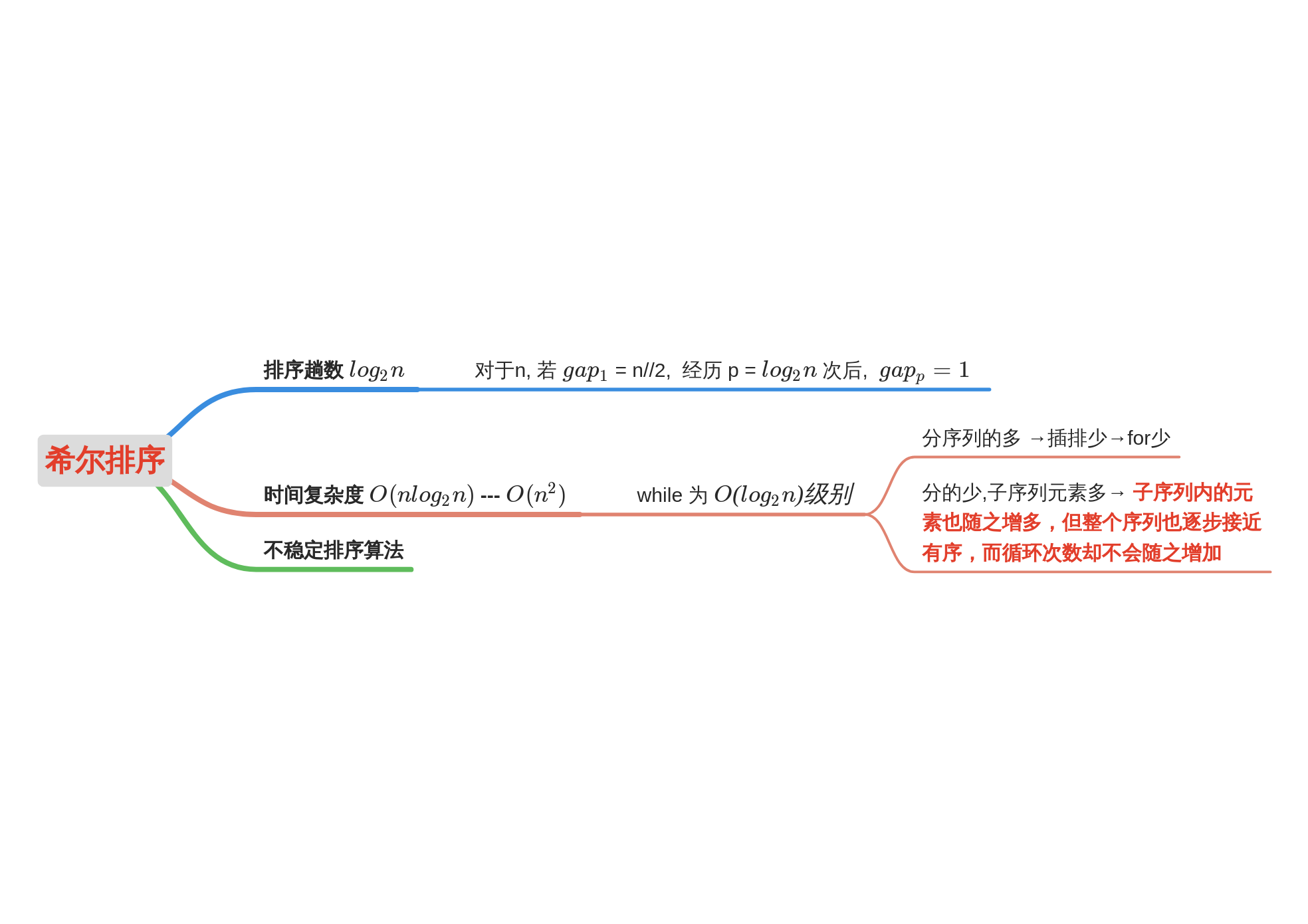
Shellsort is an optimization of insertion sort - incremental grouping insertion sort
Basic idea of Shell Sort:
The whole sequence is divided into several subsequences according to a certain interval, and each subsequence is inserted and sorted respectively. Then gradually narrow the interval for the next round of molecular sequence and insertion sequencing. Insert sort the entire sequence until the last round of sorting interval is 1.
-
First, the whole record sequence to be sorted is divided into several subsequences for direct insertion sorting. When the records in the whole sequence are "basically orderly", all records are directly inserted and sorted in turn.
-
Steps:
- Firstly, an element interval number gap is determined, and then the sequence participating in sorting is divided into several subsequences from the first element according to this interval number, that is, all elements separated by gap are regarded as a subsequence, and some sort method is used for insertion sorting in each subsequence.
- Then reduce the number of intervals, and divide the whole sequence into several subsequences according to the new number of intervals, and then sort each subsequence respectively, and so on until the number of intervals gap = 1.
- code implementation
def shellSort(arr):
size = len(arr)
gap = size // 2 # initial gap
while gap > 0: # Until gap== one
for i in range(gap, size): #Insert sort
temp = arr[i]
j = i
while j >= gap and arr[j - gap] > temp:
arr[j] = arr[j - gap]
j -= gap
arr[j] = temp
gap = gap // 2
return arr
- algorithm analysis
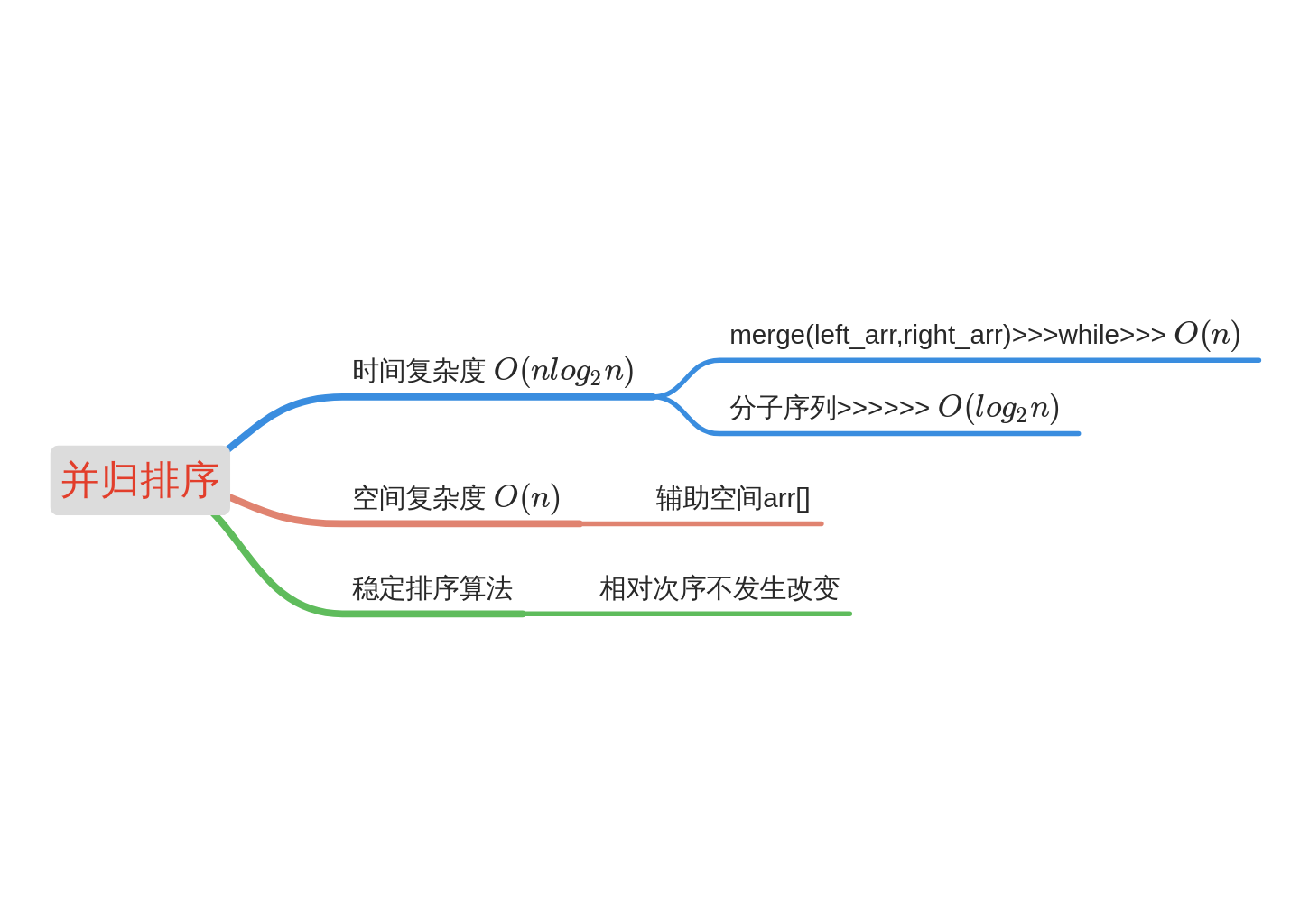
2.6 merge sort
Basic idea of Merge Sort:
Using the classical divide and conquer strategy, the current sequence is recursively divided into two halves. Then the ordered sequences are merged in pairs, and finally merged into an ordered sequence.
- Steps:
- Initially, the n records in the sequence to be sorted are regarded as n ordered subsequences (each subsequence is always ordered), and the length of each subsequence is 1.
- Merge the ordered subsequences in the current sequence group. After completion, the number of sorting sequences in the sequence group is halved and the length of each subsequence is doubled.
- Repeat the above operation for the ordered subsequence with double length, and finally get an ordered sequence with length n.
- code implementation
# Top down recursion
def merge(left_arr, right_arr): #Merge left and right subsequences
arr = []
while left_arr and right_arr:
if left_arr[0] <= right_arr[0]: # Regard the left and right sequences as the stack with the top of arr[0]
arr.append(left_arr.pop(0)) #Which one is smaller on the left and right enters the arr[] stack
else:
arr.append(right_arr.pop(0))
if left_arr: #Handling redundant elements
arr.append(left_arr.pop(0))
if right_arr:
arr.append(right_arr.pop(0))
return arr
def mergeSort(arr):
n = len(arr)
if n < 2:
return arr
mid = n // 2
left_arr = arr[:mid]
right_arr = arr[mid:]
return merge(mergeSort(left_arr),mergeSort(right_arr)) #recursion
- algorithm analysis
2.7 quick sort
Basic idea of Quick Sort:
The unordered sequence is divided into two independent sequences by one-time sorting. The value of the first sequence is smaller than that of the second sequence. Then the two subsequences are arranged recursively to achieve the order of the whole sequence
- step
-
Pick out an element from the sequence, which is called "pivot";
-
Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition exits, the benchmark is in the middle of the sequence. This is called partition operation;
-
Recursively sorts subsequences that are smaller than the reference value element and subsequences that are larger than the reference value element
-
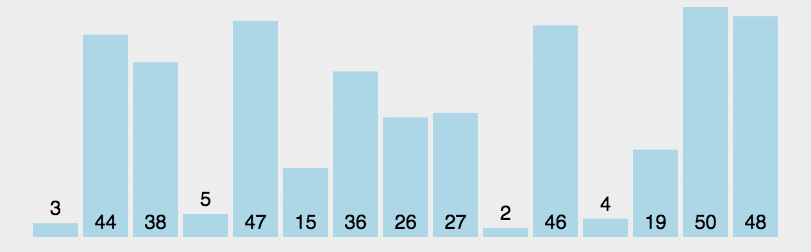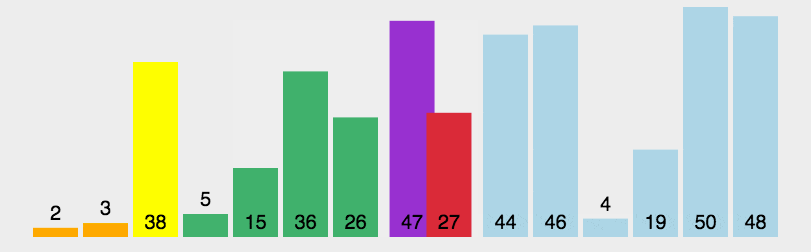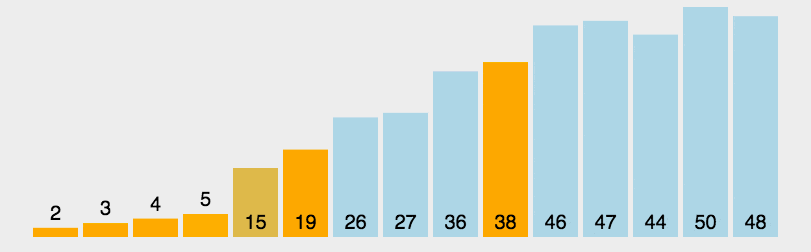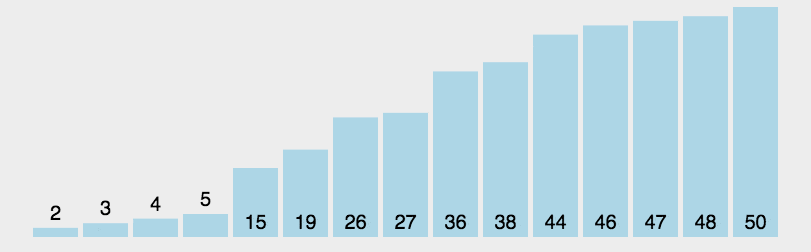
- code implementation
import random
def partition(arr: [int], low: int, high: int):
i = random.randint(low, high)
arr[i], arr[high] = arr[high], arr[i]
x = arr[high]
i = low - 1
for j in range(low, high):
if arr[j] <= x:
i += 1
arr[i], arr[j] = arr[j], arr[i]
arr[i + 1], arr[high] = arr[high], arr[i + 1]
return i + 1
def quickSort(arr, low, high):
if low < high:
pi = partition(arr, low, high)
quickSort(arr, low, pi - 1)
quickSort(arr, pi + 1, high)
return arr
A good article on fast scheduling: https://www.jianshu.com/p/2b2f1f79984e
- algorithm analysis
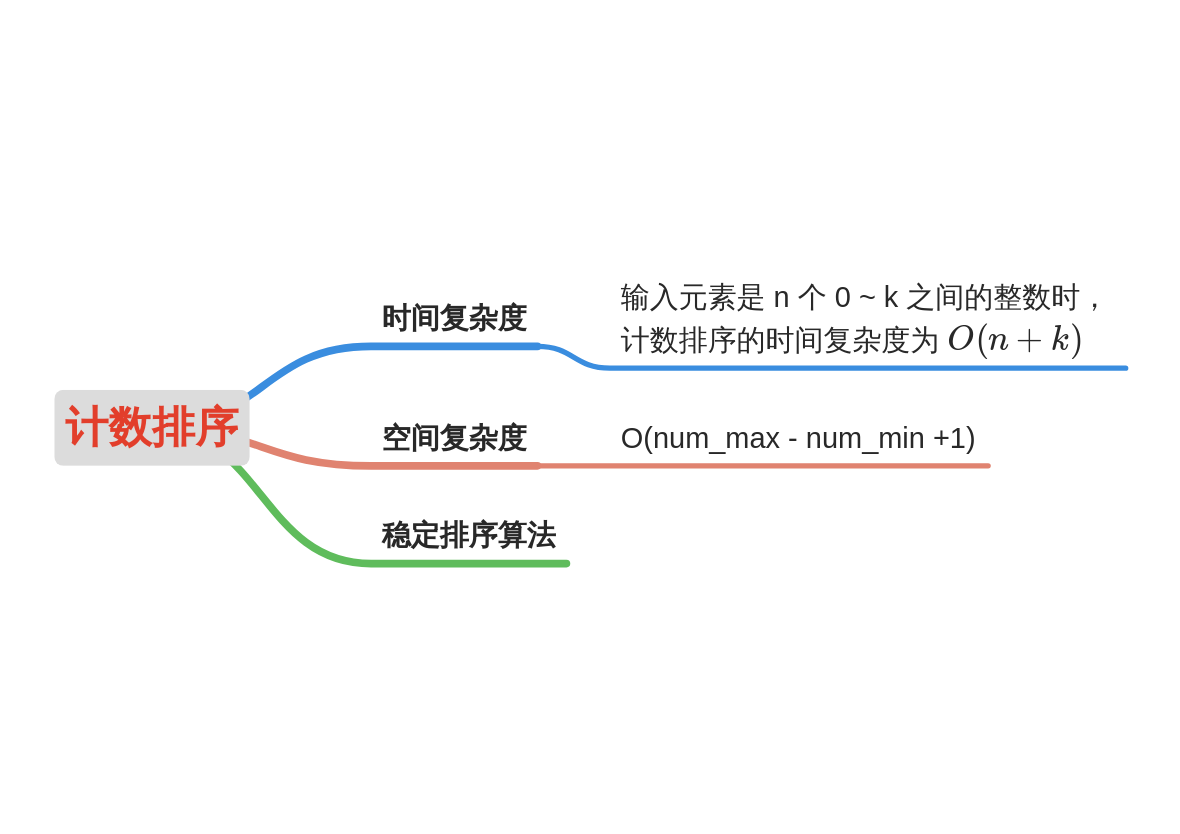
2.8 counting and sorting
Basic idea of Counting Sort:
Use an additional array counts, where the i-th element counts[i] is the number of elements whose value in the array arr to be sorted is equal to I. Then arrange the elements in the ARR in the correct position according to the array counts.
-
step
- Find the maximum and minimum elements in the array to be sorted.
- Count the number of occurrences of each element with value i in the array and store it in item i of the array.
- All counts are accumulated (starting from the first element in counts, each item is accumulated with the previous item).
- Reverse fill the target array: put each element I in the count [i] item of the new array, and count [i] - = 1 for each element.
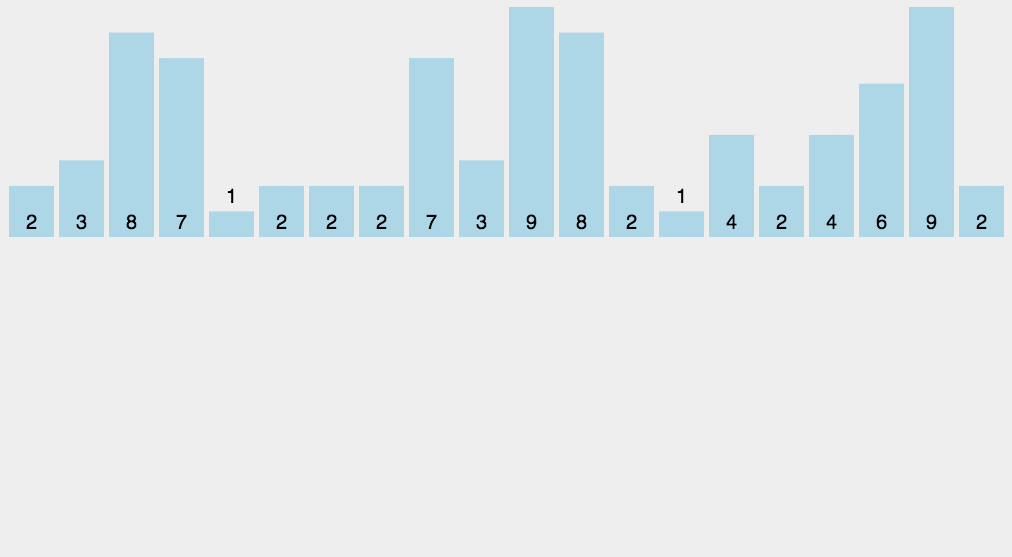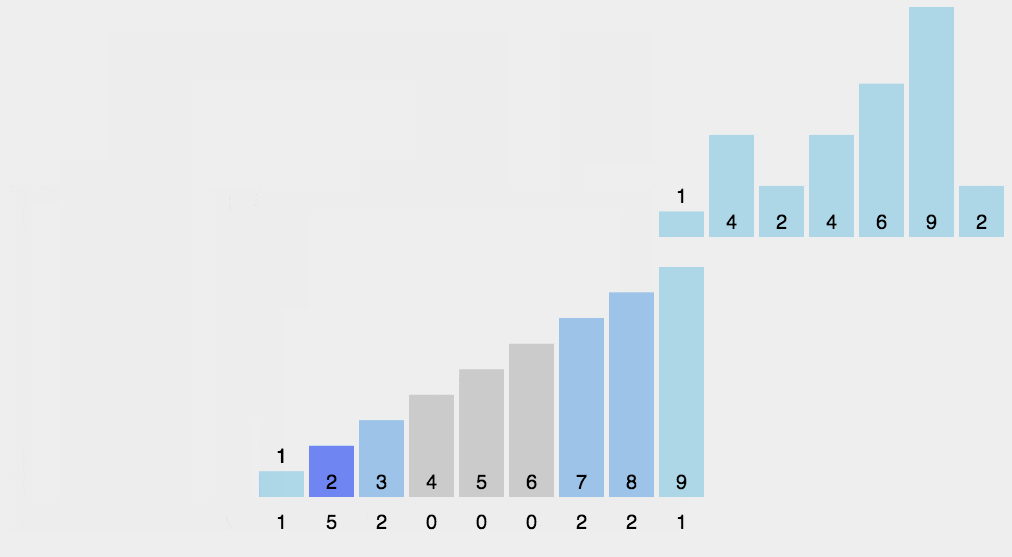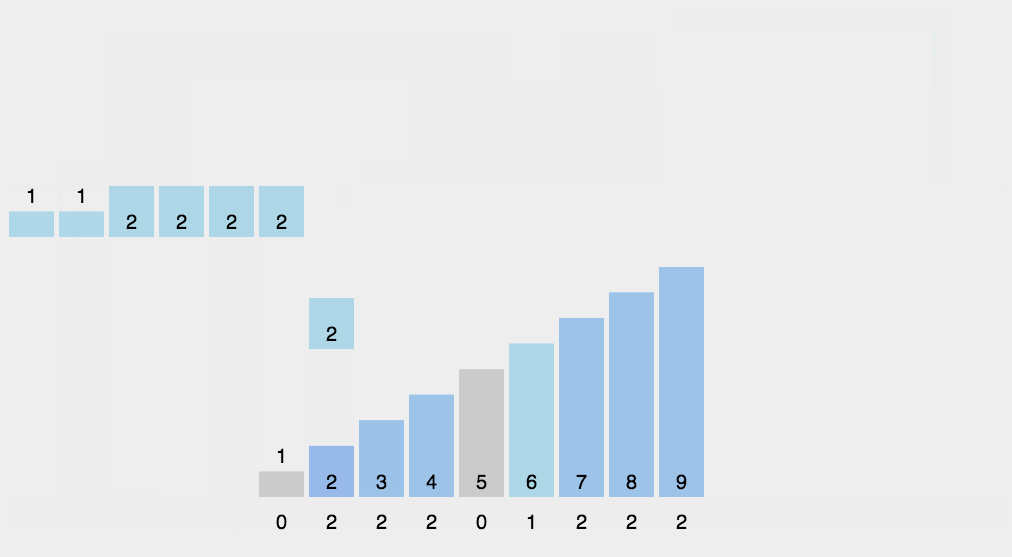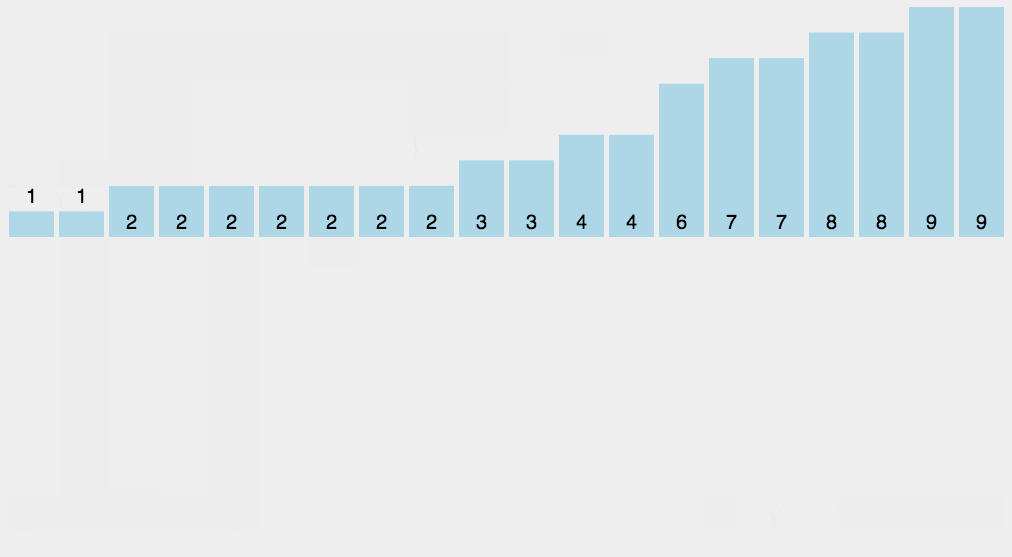
- python implementation
def countingSort(arr):
arr_min, arr_max = min(arr), max(arr) #Calculate the maximum and minimum elements of an integer and find the number of all elements in its period
gap = arr_max - arr_min + 1
size = len(arr)
counts = [0 for _ in range(gap)]
for num in arr: #Count each element in each interval
counts[num - arr_min] += 1
for j in range(1,gap): #After counting, replace count [] each element with class plus quantity
counts[j] += counts[j - 1]
res = [0 for _ in range(size)] #Use extra space to store sorting results
for i in range(size - 1, -1, -1):
res[counts[arr[i] - arr_min] - 1] = arr[i]
counts[arr[i] - arr_min] -= 1
return res
arr = [1,2,3,9,6,5,4,8,6,9,2,55]
countingSort(arr)
- algorithm analysis
2.9 bucket sorting
Basic idea of Bucket Sort:
The unordered array is divided into several "buckets", and the elements of each bucket are sorted separately.
-
step
The interval is divided into n sub intervals of the same size, and each interval is called a bucket.
Traverse the array and load each element into the corresponding bucket.
The elements in each bucket are sorted separately (using algorithms such as insertion, merging, fast sorting, etc.).
Finally, merge the elements in the bucket in order.
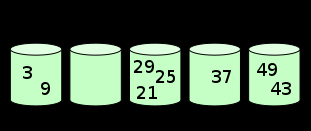
- python implementation
def insertionSort(arr):
for i in range(1, len(arr)):
temp = arr[i]
j = i
while j > 0 and arr[j - 1] > temp:
arr[j] = arr[j - 1]
j -= 1
arr[j] = temp
return arr
def bucketSort(arr, bucket_size = 5):
arr_min, arr_max = min(arr), max(arr)
bucket_count = (arr_max - arr_min) // bucket_size + 1
buckets = [[] for _ in range(bucket_count)]
for num in arr:
buckets[(num - arr_min) // bucket_size].append(num)
res = []
for bucket in buckets:
insertionSort(bucket)
res.extend(bucket)
return res
- algorithm analysis
2.10 cardinality sorting
Basic idea of Radix Sort:
Cut integers into different numbers according to the number of bits, and then compare and sort them according to each number of bits.
-
step
-
The radix sorting algorithm can adopt "least significant digital first" or "most significant digital first". The most commonly used is "least significant digital first".
Let's take the lowest priority method as an example:.- Traverse the array elements, get the maximum element of the array, and get the number of bits.
- Sort the array elements with bit elements as indexes.
- Merge arrays.
- After that, take the ten bits, hundred bits,..., up to the highest value of the maximum value element as the index, sort, merge the array, and finally complete the sorting.
-
-
python
def radixSort(arr):
size = len(str(max(arr))) #Find the number of bits of the largest element
for i in range(size): #Sort bit size
buckets = [[] for _ in range(10)]
for num in arr:
buckets[num // (10**i) % 10].append(num)
arr.clear()
for bucket in buckets:
for num in bucket:
arr.append(num)
return arr
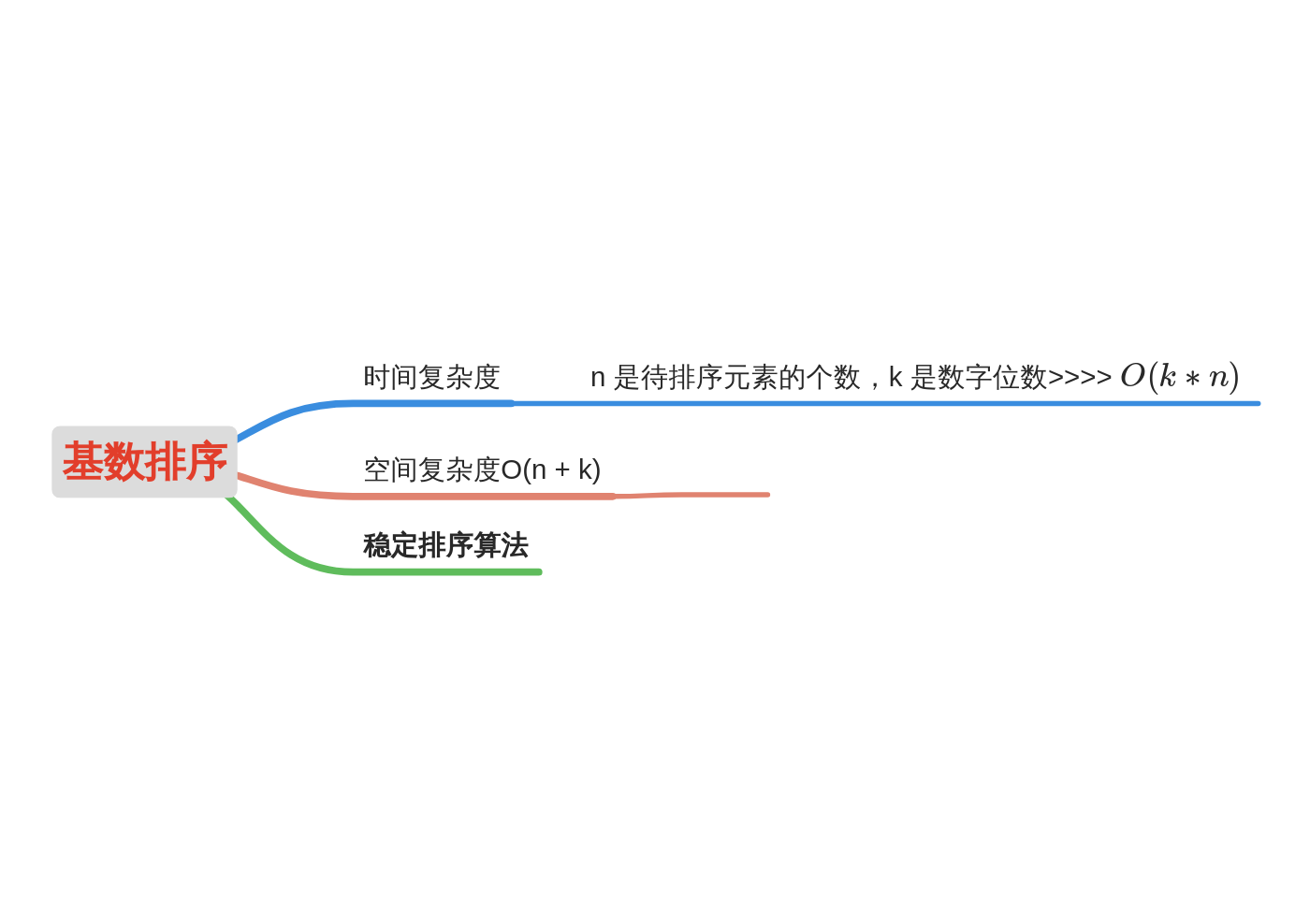
Insertion, bubbling, merging, counting, cardinality, and bucket sorting are stable
Select \ hill \ fast, heap sort is unstable
2.11 related topics
- Idea: first establish the mapping of arr2 value to subscript > > > user defined sorting
class Solution {
public:
vector<int> relativeSortArray(vector<int>& arr1, vector<int>& arr2) {
unordered_map<int, int> rank;
for (int i = 0; i < arr2.size(); ++i) {
rank[arr2[i]] = i;
}
sort(arr1.begin(), arr1.end(), [&](int x, int y) {
if (rank.count(x)) {
return rank.count(y) ? rank[x] < rank[y] : true;
}
else {
return rank.count(y) ? false : x < y;
}
});
return arr1;
}
}
Custom function --------------------- O(nlogn)
Consider the key solution of sort in python:
return sorted(arr1, key = lambda x:(0, arr2.index(x)) if x in arr2 else (1, x))
- Idea 2: count ------------ O(n)
class Solution:
def relativeSortArray(self, arr1: List[int], arr2: List[int]) -> List[int]:
ans, count = [], [0]*1001
for arr in arr1:
count[arr] += 1
for arr in arr2:
while count[arr] > 0:
ans.append(arr)
count[arr] -= 1
for arr in range(1001):
while count[arr] > 0:
ans.append(arr)
count[arr] -= 1
return ans
- Method 1: user defined sorting + interval trade-off
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort(key = lambda x:x[0])
ans, start, farthest = [], -1, -1
for interval in intervals:
left, right = interval[0], interval[1]
if left <= farthest: #If the next interval overlaps with
farthest = max(farthest, right)
else:
if farthest != -1:
ans.append([start, farthest])
start = left
farthest = right
ans.append([start, farthest])
return ans
- Idea 2: difference
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
ans, events = [], []
for interval in intervals:
events.append([interval[0], 1])
events.append([interval[1] + 1, -1])
events.sort(key = lambda x:(x[0],x[1]))
covering = 0
for event in events:
if covering == 0:
start = event[0]
covering += event[1]
if covering == 0:
ans.append([start, event[0] - 1])
return ans
Idea: fast queue > > > > number of left and right sides of partition
class Solution:
import random
def findKthLargest(self, nums: List[int], k: int) -> int:
return self.quickSort(nums, 0, len(nums) - 1, len(nums) - k)
def quickSort(self, arr, l, r, index):
if l >= r:
return arr[l]
pivot = self.partition(arr, l, r)
if index <= pivot:
return self.quickSort(arr, l, pivot, index)
else:
return self.quickSort(arr,pivot + 1, r, index)
def partition(self, a, l, r):
pivot = random.randint(l, r)
pivotVal = a[pivot]
while l <= r:
while a[l] < pivotVal:
l += 1
while a[r] > pivotVal:
r -= 1
if l == r:break
if l < r:
a[l], a[r] = a[r], a[l]
l += 1
r -= 1
return r
task
- Idea: the minimum carrying capacity of the ship should at least be equal to or greater than the heaviest package, namely max(weights). At most, all packages can be transported at one time, that is, sum(weights). The carrying capacity of the ship is between [max(weights), sum(weights)]. > > > At the same time, first calculate the transportation days with carrying capacity mid = (high + low) // 2, and then compare it with D to narrow the interval:
class Solution:
def shipWithinDays(self, weights: List[int], days: int) -> int:
low, high = max(weights), sum(weights)
while low < high:
mid = low + (high - low) // 2
# How many days does it take to calculate the load as mid
cur = 0 # Weight of current days
day_mid = 1 # Current days
for weight in weights:
if weight + cur > mid:
day_mid += 1
cur = 0
cur += weight
if day_mid > days: #If the number of days exceeds, increase the load
low = mid + 1
else:
high = mid
return low
class Solution:
def findMin(self, nums: List[int]) -> int:
left, right = 0, len(nums) - 1
while left < right:
mid = left + (right - left)//2
if nums[mid] < nums[right]:
right = mid
elif nums[mid] == nums[right]:
right -= 1
else:
left = mid + 1
return nums[right]
reference material
1.https://algo.itcharge.cn Algorithm clearance manual (LeetCode)