1. KMP
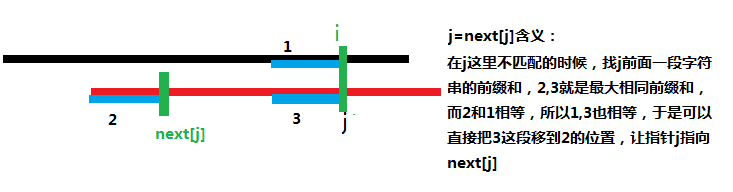
Next array: what is the length of the longest common prefix for each location of the storage pattern string, and then when moving the pattern string pointer, when p[j]!=When s[i] (p mode string, s main string), pointer J can move quickly, that I s, j=next[j].
Why?
Title: Activities - AcWing
#include<iostream>
#include<string>
using namespace std;
const int N=1e5+10,M=1e6+10;
int ne[N];
int main()
{
int n,m;
char p[N],s[M];
cin>>n>>p+1>>m>>s+1;
//next array for pattern string p
for(int i=2,j=0;i<=n;i++)
{
while(j&&p[i]!=p[j+1])
j=ne[j];
if(p[i]==p[j+1])
j++;
ne[i]=j;
}
//Match, match from subscript 1
for(int i=1,j=0;i<=m;i++)
{
while(j&&s[i]!=p[j+1])
j=ne[j];
if(s[i]==p[j+1])//The current two characters are equal, moving forward
j++;
if(j==n)//Match Successful
{
cout<<i-n<<' ';//Title requires subscripts to start at 0
j=ne[j];//Next time you continue looking backwards, where the pattern string will move to
}
}
return 0;
}2. Single Chain List
Each node has a pointer to the next node adjacent to it.
The idea is to open two arrays, val[],ne[] to store the value corresponding to each subscript IDX and the location of the next node it points to, IDX to store the subscript corresponding to each node, IDX to each adjacent node is not continuous, each node to access its next node is to get its next node pointing to that through the idx of the current node, that is, ne[idx].
Template:
#include<iostream>
using namespace std;
const int M=100;
int head,idx;
int val[M],ne[M];
void init()
{
head=-1;//head node
idx=0;//Next Node to which Head Node Points
}
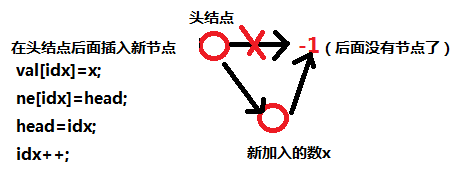
//Insert a new node after the head node
void insert_head(int x)
{
val[idx]=x;
ne[idx]=head;//At this point, the newly inserted node points to the next node that the header node was originally pointing to. Now the header node points to it
head=idx;//Head Node Points to Current Node
idx++;
}
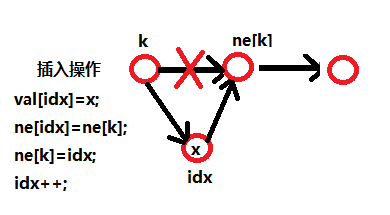
//Insert x after subscript k
void insert_x(int k,int x)
{
//The current insertion of the node's variation, idx is only used to represent the current point's location, not the subscript representation, we visit each
//Nodes are accessed through the ne array, where the address IDX of the next node is stored (each node has a different idx)
//And values,
val[idx]=x;
ne[idx]=ne[k];
//The k-th node points to a node that changes
ne[k]=idx;
idx++;
}
//Delete the node after the k-point
void dele(int k)
{
ne[k]=ne[ne[k]];
}
int main()
{
int m,x,k;
char ch;
cin>>m;
while(m--)
{
cin>>ch;
init();//Don't forget to initialize
if(ch=='H')
{
cin>>x;
insert_head(x);
}
else if(ch=='D')
{
cin>>k;
if(k==0)//Delete the header node, that is, make it the node that the header node points to
head=ne[head];
dele(k-1);//k-1 Subscripts start with 1, we start with 0
}
else
{
cin>>k>>x;
insert_x(k-1,x);
}
}
for(int i=head;i!=-1;i=ne[i])//Traversal starts at the first node, which is the next node to which the header node points
{
cout<<val[i]<<' ';
}
return 0;
}3. Double Chain List
#include<iostream>
#include<string>
using namespace std;
const int M=1e5+10;
int val[M],l[M],r[M],idx;
void inti()
{
l[1]=0;//head node
r[0]=1;//End Point
idx=2;//Subscript starts at 2 because 0 and 1 are used as left and right endpoints
}
//Insert number x to the right of the k-th node. If a new node is required to be inserted to the left of K, the value passed in is l[k], not k-1, because subscripts are not continuous
void insert(int k,int x)
{
val[idx]=x;
r[idx]=r[k];//Right Node Pointing to Newly Joined Node
l[idx]=k;//Left node pointed to by newly joined node
l[r[k]]=idx;//!!!Order cannot be reversed
r[k]=idx;//The right node that section k points to becomes a newly added node
idx++;
}
//Delete the k th point
void remove(int k)
{
r[l[k]]=r[k];//Let K's left and right nodes point to each other
l[r[k]]=l[k];
}
int main()
{
int m,x;
string s;
cin>>m;
inti();
while(m--)
{
cin>>s;
if(s=="L")
{
cin>>x;
insert(0,x);//Insert number x at the leftmost end
}
else if(s=="R")
{
cin>>x;
insert(l[1],x);//Insert at the far right, after the end
}
else if(s=="D")//Delete the number of KTH inserts
{
int k;
cin>>k;
remove(k+1);
}
else if(s=="IL")
{
int k;
cin>>k>>x;
insert(l[k+1],x);//Insert a number to the left of the k-th inserted number, passing in l[k]!!!!
}
else
{
int k;
cin>>k>>x;
insert(k+1,x);
}
}
for(int i=r[0];i!=1;i=r[i])
{
cout<<val[i]<<' ';
}
cout<<endl;
return 0;
}4. Stack
Basic features: FIFO
Several operations: //insert int x; stk[++tt]=x; //Eject from top of stack tt--; //Determine whether it is empty if(tt>0) not empty; else empty; //Gettop stk[tt];
Analog stack:
#include<iostream>
#include<string>
using namespace std;
const int N=1e5+10;
int stk[N],tt=-1;//Subscript starts at 0
int main()
{
int m,x;
string str;
cin>>m;
while(m--)
{
cin>>str;
if(str=="push")
{
cin>>x;
//Insert elements to the top of the stack
stk[++tt]=x;
}
else if(str=="pop")
tt--;//Pop an element from the top of the stack
else if(str=="empty")
{
if(tt<0)
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
else
{
//Query top element
cout<<stk[tt]<<endl;
}
}
return 0;
}3302.Expression Evaluation - AcWing Test Gallery
The idea is to simulate two stacks, one to store numbers and one to store operators. When encountering operators, first determine the priority of the current operator and the top operator. If less than or equal, first operate the top operator on the stack, and then put the current operator on the stack.Otherwise, go directly to the stack. For brackets, we set the priority of brackets to the lowest. When the top of the stack is'(', the priority of the next operator must be greater than'('), so let this operator go directly to the stack, and then calculate the values in brackets as above until')', and let'('go out of the stack.
#include<iostream>
#include<string>
#include<map>
using namespace std;
const int N=1e5;
int num[N],t_num=-1,t_op=-1;;
char op[N];
map<char,int> h={{'+',1},{'-',1},{'*',2},{'/',2}};//Priority of easy comparison operator, default value not set is 0
void eval()
{
int a=num[t_num--];
int b=num[t_num--];
char ch=op[t_op--];
int res=0;
//Notice here the order in which a and B work. Elements go upside down into the stack, but we do this from the front to the back.
if(ch=='+')
res=b+a;
else if(ch=='-')
res=b-a;//Can't be a-b!!!
else if(ch=='*')
res=b*a;
else
res=b/a;
num[++t_num]=res;//Stack results
}
int main()
{
string str;
cin>>str;
int len=str.length();
for(int i=0;i<len;i++)
{
if(isdigit(str[i]))
{
int temp=0,j=i;
while(j<len&&isdigit(str[j]))
{
temp=temp*10+str[j]-'0';
j++;
}
num[++t_num]=temp;//Number stacking
i=j-1;
}
else if(str[i]=='(')
{
op[++t_op]='(';
}
else if(str[i]==')')//Encounter right parenthesis, calculate the values inside first
{
while(op[t_op]!='(')
eval();
t_op--;//Put the left parenthesis on the stack
}
else
{
while(t_op>=0&&h[op[t_op]]>=h[str[i]])
eval();
op[++t_op]=str[i];//High priority direct stacking
}
}
while(t_op>=0)
eval();//Calculate the last remaining number
cout<<num[t_num]<<endl;
return 0;
}5. Queues
Analog Queue
#include<iostream>
#include<string>
using namespace std;
const int N=1e5+10;
int q[N],hh,tt=-1;
int main()
{
int m,x;
string s;
cin>>m;
while(m--)
{
cin>>s;
if(s=="push")
{
cin>>x;
q[++tt]=x;//Insert an element at the end of the queue
}
else if(s=="pop")//Pop a number from the opposite end
hh++;
else if(s=="empty")
{
if(hh>tt)
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
else
{
cout<<q[hh]<<endl;//Query Header Elements
}
}
return 0;
}Monotonic stack: Elements enter and exit from the end of the queue. Elements in the stack are monotonic.
Application: Find the first number smaller than x to the left of X.
The idea: Every time before adding an element, keep looking for the number on the left that is larger or equal to it to pop up (because we are looking for the first number on the left that is smaller than it, so there is no need to compare all the numbers that are larger than the new added element with the next one). Finally, if there is a number smaller than it, output the number, and then put it on the stack yourself.
#include<iostream>
using namespace std;
const int N=1e5+10;
int stk[N],tt,n;
int main()
{
cin>>n;
int x;
for(int i=0;i<n;i++)
{
cin>>x;
//Determines if a smaller number exists before the current number of inputs, if the number is output, otherwise the number of inputs is stacked
while(tt&&stk[tt]>=x)//Pop a number larger than x out of the stack
tt--;
if(tt&&stk[tt]<x)
cout<<stk[tt]<<' ';
else
cout<<-1<<' ';
stk[++tt]=x;
}
return 0;
}Monotonic Queue: A queue whose head and tail can be queued, but only the tail can be queued. All the numbers in the queue are monotonically arranged, increasing or decreasing.
Application: Slide the window, each time outputting the minimum and maximum of all the numbers in the current window range.
Idea: First decide if the number of counterparts should leave the queue first (it may not be in the window range), before adding the number of new frames to the queue, eject the number larger than that from the end of the queue, and then output the corresponding value of the counterpart. Start with the tail and eject the number larger than x (the minimum value of the next window will only occur between X and the newly added value).Finally, no matter how x is added from behind, because for the window in which X is selected by a box, we don't know if x will be the minimum value in that window.
#include<iostream>
using namespace std;
const int N=1e6+10;
int n,k,a[N],q[N];//q contains the subscript for the corresponding value
int main()
{
int tt=-1,hh=0;
scanf("%d%d",&n,&k);
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
for(int i=0;i<n;i++)
{
//First decide if the leader wants to leave the team
if(hh<=tt&&i-k+1>q[hh])
hh++;//The team leader came out
while(hh<=tt&&a[q[tt]]>=a[i])
tt--;
q[++tt]=i;//The subscript for the current value should be queued first because it is possible that it will be the minimum value and the previous queue will be emptied
if(i-k+1>=0)//To make a special judgement, start outputting the minimum value when the number of boxes is k
printf("%d ",a[q[hh]]);
}
printf("\n");
//Maximum
tt=-1,hh=0;
for(int i=0;i<n;i++)
{
if(hh<=tt&&i-k+1>q[hh])//i-k+1 is the subscript for the first number in the sliding window
hh++;
while(hh<=tt&&a[q[tt]]<=a[i])
tt--;
q[++tt]=i;
if(i-k+1>=0)
printf("%d ",a[q[hh]]);
}
printf("\n");
return 0;
}Think questions:
1,Problem - B - Codeforces (Unofficial mirror site, accelerated for Chinese users)
Title: Delete as many numbers as possible so that nonemprinsic numbers remain. (Title guarantees existence)
Think: For numbers with 1, 4, 6, 8, 9, we can always leave only one of them; otherwise we can only leave 3, 5, 7
These three numbers, if 3, 5, 7 all exist at the same time for those with a length greater than 3, then they must be able to form
Two-digit nonprime numbers;If only one or two of the three numbers exist, there must be duplicate two digits, which are also non-prime numbers.
So just decide if any two numbers they make up are non-prime numbers.
#include<iostream>
const int M=55;
using namespace std;
int Isprime(int x)
{
for(int i=2;i*i<=x;i++)
{
if(x%i==0)
return 0;
}
return 1;
}
int main()
{
int t,k,a[M],ans,sum;
scanf("%d",&t);
while(t--)
{
int flag=0;
scanf("%d",&k);
for(int i=0;i<k;i++)
{
scanf("%1d",&a[i]);
//If there is one of the numbers 1, 4, 6, 8, 9, you can definitely end up with just this number
if(!flag)
{
if(a[i]==1||a[i]==4||a[i]==6||a[i]==8||a[i]==9)
{
sum=1;
ans=a[i];
flag=1;
}
}
}
if(!flag)
{
for(int i=0;i<k;i++)
{
//Otherwise, find any two numbers from the remaining numbers that make up a nonprime number
for(int j=i+1;j<k;j++)
{
int num=a[i]*10+a[j];
if(!Isprime(num))
{
sum=2;
ans=num;
flag=1;
break;
}
}
if(flag)
break;
}
}
printf("%d\n%d\n",sum,ans);
}
return 0;
} 2, B. Shifting Sort
Idea: Traverse through all elements, find the smallest median value of all elements after the first element each time (marked as idx below), and put [i,idx]All elements in the array are moved one bit backwards to move this smallest element to the position of the first element. After this operation, the smallest element of all elements in the array that follow I is moved to the front. So the general idea is: let the smallest elements in the whole array go out one by one.
#include<iostream>
#include<vector>
#include<utility>
using namespace std;
typedef pair<int,int> pii;
int main()
{
int t,n;
cin>>t;
while(t--)
{
cin>>n;
vector<int>a(n+1);
vector<pii>action;
int sum=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<n;i++)
{
int min_pos=i;//Subscript holding minimum element
for(int j=i+1;j<=n;j++)//Find the smallest value in the element after i
{
if(a[min_pos]>a[j])
min_pos=j;
}
if(min_pos>i)
{
action.push_back({i,min_pos});
//Move the minimum value to the top of the [i,min_pos] interval and the other values one bit backward
int temp=a[min_pos];
for(int k=min_pos;k>i;k--)
{
a[k]=a[k-1];//Move Backward
}
a[i]=temp;
}
}
cout<<action.size()<<'\n';
for(auto &lr:action)
{
cout<<lr.first<<' '<<lr.second<<' '<<lr.second-lr.first<<'\n';
}
}
return 0;
}E1. Permutation Minimization by Deque
Topic: A set of integers can only take the first number of the group at a time, take it out and put it in a new group of numbers, only in the first or last two places, to make up the smallest dictionary ordinal array.
Idea: Use a deque Container to store the first digit of the current array and the first digit that has been taken out and placed in another container each time. If it is less than this, place the number at the first q.push_front(x) of the container, otherwise put it at the end q.push_back(x).
#include<iostream>
#include<deque>
using namespace std;
const int M=2e5+10;
deque<int> q;
int main()
{
int t,n;
int p[M];
cin>>t;
while(t--)
{
cin>>n;
q.clear();
for(int i=0;i<n;i++)
{
cin>>p[i];
}
int head=p[0];
q.push_front(head);
for(int i=1;i<n;i++)
{
if(p[i]<head)
{
q.push_front(p[i]);
head=p[i];
}
else
{
q.push_back(p[i]);
}
}
for(deque<int>::const_iterator iter=q.begin();iter!=q.end();iter++)
cout<<*iter<<" ";
cout<<endl;
}
return 0;
}